Doç. Dr. Özgür Baştürk
Ankara Üniversitesi, Astronomi ve Uzay Bilimleri Bölümü
obasturk at ankara.edu.tr
http://ozgur.astrotux.org
Bu derste neler öğreneceksiniz?¶
Frekans Analizi¶
- Periyodik Fonksiyonlar ve Fourier Serileri
- Fourier-Dönüşümleri
- Konvolüsyon
- Korelasyon
- Örneklendirme Teoremi
- Süreksiz Fourier Dönüşümü
- Spektral Yoğunluk ve Güç Spektrumu
- Klasik Periyodogram
- Düzensiz Aralıklı Yapılan Gözlemler ve Nyquist Limiti
- Lomb Scargle Periyodogramı
- Spektral Sızma
- Örnek Frekans Analizi
- Kaynaklar
Periyodik Fonksiyonlar ve Fourier Serileri¶
$T$ dönemle kendini tekrar eden fonksiyonlara periyodik fonksiyonlar denir.
$$ f (t + T) = f(t) $$$T$ periyoduna sahip bir Fourier Serisi, frekansı $\nu = \frac{1}{T}$ temel frekansının tam katları olan sinüsoidal fonksiyonların sonsuz toplamıdır.
$$ g(t) = a_0 + \sum_{m = 1}^{\infty} a_m cos(\frac{2 \pi m t}{T}) + \sum_{n = 1}^{\infty} b_n sin(\frac{2 \pi n t}{T}) = \sum_{m = 0}^{\infty} a_m cos(\frac{2 \pi m t}{T}) + \sum_{n = 1}^{\infty} b_n sin(\frac{2 \pi n t}{T}) $$Periyodik fonksiyonun y eksenindeki kayma miktarını $a_0$ ve farklı frekanstaki her bir sinüs / kosinüs fonksiyonuna verilecek ağırlığı $a_m$ ve $b_n$ katsayıları belirler. Dolayısı ile periyodik fonksiyonu Fourier serisine açmak, bu katsayıları belirlemektir. Birinci katsayı fonksiyonun ortalama değeridir.
$$ a_0 = \frac{1}{T} \int_0^T f(t) dt $$$$ a_m = \frac{2}{T} \int_0^T f(t) cos(\frac{2 \pi m t}{T}) dt $$$$ b_n = \frac{2}{T} \int_0^T f(t) sin(\frac{2 \pi n t}{T}) dt $$Örnek: Kare Dalganın Fourier Serisine Açılımı¶
Kare dalga fonksiyonu için yukarıdaki formüller kullanılarak elde edilebilecek katsayılar kullanılarak Fourier serisi oluşturulabilir.
$$ a_0 = \frac{1}{2} $$$$ a_m = 0, m = 1,2,... $$$$ b_n = \frac{2}{\pi n}, n = 1,3,5,... $$$$ b_n = \frac{2}{\pi n}, n = 2,4,6,... $$Kare dalga örneğinde Fourier serisini ilk iki terim ($a_0 = 0$ ve $b_1 = \frac{2}{\pi}$) alındığında,
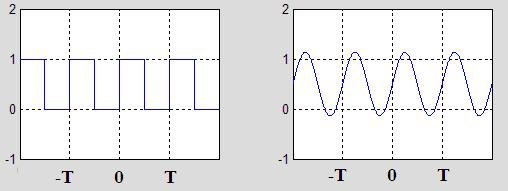
üç terimi ($a_0$, $b_1$, $b_3$) alındığında,
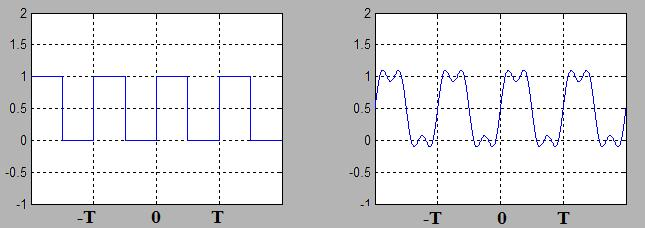
ilk yedi terimi alındığında ise
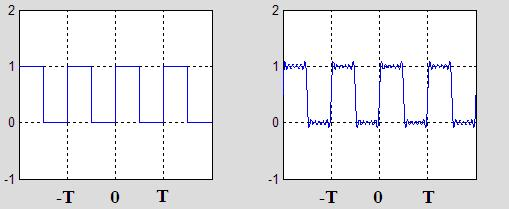
fonksiyonları elde edilir. Seriden sonsuz terim alınması durumunda kare dalga fonksiyonuna ulaşılır.
Fourier Serilerinin Kompleks İfadesi¶
Periyodik tüm fonksiyonlar ($f(t + T) = f(t)$) bu şekilde sinüsoidal fonkiyonların br toplamı olarak ifade edilebilir. Bir fonksiyonun Fourier serisine açılımından ne kadar çok sayıda terim alınırsa fonksiyonun kendisine o kadar yakınsanır.
Fourier serileri Euler eşitliğinden yararlanılarak kompleks formda da yazılabilir.
$$ e^{i t} = cos t + i sin t , i = \sqrt{-1} $$$$ g(t) = \sum_{-\infty}^{\infty} c_n e^{i \frac{2 \pi n t}{T}} $$Bu durumda $c_n$ katsayıları aşağıdaki ifade ile hesaplanır.
$$ c_n = \frac{1}{T} \int_0^T f(t) e^{i \frac{2 \pi n t}{T}} dt $$Kare dalga fonksiyonu için $c_n$ katsayıları
$$ c_0 = \frac{1}{2} $$$$ c_n = \frac{2}{\pi n}, n = \pm1,\pm3,\pm5,... $$$$ c_n = 0, n = \pm2,\pm4,\pm6,... $$Örnek: Kosinüs Fonksiyonunun Fourier Serisine Açılımı¶
Aşağıdaki kosinüs fonksiyonu ($f(t) = cos (4 \pi t)$) ele alınacak olursa
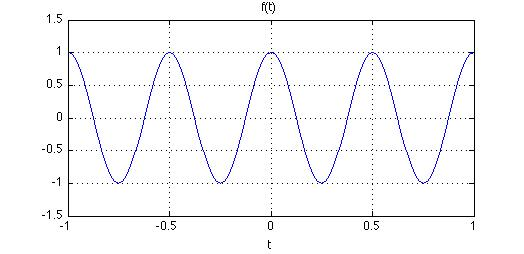
toplamın sol tarafındaki integral;
$$ \int_0^{0.5} e^{i 4 \pi t (1-n)} dt = \frac{e^{i 4 \pi t (1-n)}}{i 4 \pi (1-n)} |_0^{0.5} = \frac{1}{i 4 \pi (1-n)} = [e^{i 2 \pi (1-n)} - 1] = 0, n \ne 1 $$İntegralin sonucu $n = 1$ dışında her yerde 0, $n = 1$’de ise tanımsız görünüyor. Ancak integralin kendisi $n = 1$ için tanımsız değildir. $n = 1$ yerine integrasyondan önce konursa;
$$ c_1 = \int_0^{0.5} e^{i 4 \pi t (1-n)} dt = \int_0^{0.5} e^{i 4 \pi t (1-1)} = \int_0^{0.5} 1 dt = 0.5 $$İntegralin sağ tarafı için de aynı şey geçerli olup bu kez $n = -1$ değerinin integrasyondan önce yerine konması gerekir ki bu durumda da $c_{-1} = 0.5$ bulunur. Diğer tüm $c_n$ katsayıları 0 olur.
$c_{-1} = c_1 = 0$ yerine konursa fonksiyonun Fourier serisine açılımının fonksiyonun kendisi ile denk olduğu kolayca görülebilir.
$$ g(t) = \sum_{-\infty}^{\infty} c_n e^{i \frac{2 \pi n t}{T}} = c_1 e^{\frac{i 2 \pi t}{T}} + c_{-1} e^{\frac{-i 2 \pi t}{T}} = 0.5 (e^{i 4 \pi t} + e^{-i 4 \pi t}) = cos (4 \pi t) = f(t) $$Fourier Dönüşümleri¶
Fourier serileri herhangi bir periyodik fonksiyonu sinüsoidal fonksiyonlara dönüştürmeyi sağlar. Fourier dönüşümleri ise bu fikir alır ve periyodik olmayan fonksiyonlara da uygular. Böylece tüm fonksiyonların sinüsoidal fonksiyonların toplamı şeklinde ifade edilmesini sağlar.
$$ \mathscr{F} \{g(t)\} = G(f) = \int_{-\infty}^{+\infty} g(t) e^{-2 \pi f t} dt $$Fourier dönüşümü sonucunda elde edilen $G(f)$ fonksiyonu zamanın ($t$) değil frekansın ($f$) bir fonksyonu olup $g(t)$ fonksiyonunun $f$ frekansındaki gücünü gösterir. $G(f)$, $g(t)$'nin "spektrumu" olarak da adlandırılır. $g(t)$ fonksiyonuna $G(f)$ fonksiyonundan ters Fourier dönüşümü ile geçilir.
$g(t)$ ve $G(f)$ ikilisine ise bir Fourier çifti adı verilir.
$$ g \Longleftrightarrow G $$Örnek: Kutu Fonksiyonunun Fourier Dönüşümü¶
Astronomide özellikle gözlem çerçevelerini ifade etmek için kullanılan kutu fonksiyonu, kare dalga fonksiyonunun özel bir halidir. Foıksiyon, $[-T/2 , T/2]$ aralığında $A$’ya $|t| \gt T/2$ için ise $0$’a eşittir.
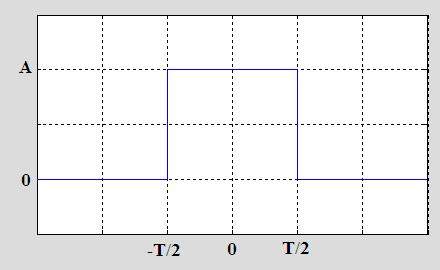
Fourier dönüşümünün tanımı kutu fonksiyonu üzerine uygulanacak olursa
$$ \mathscr{F} \{g(t)\} = G(f) = \int_{-\infty}^{+\infty} g(t) e^{-2 \pi f t} dt $$$$ \mathscr{F} \{g(t)\} = G(f) = \int_{-T/2}^{+T/2} A e^{-2 \pi f t} dt = \frac{A}{-2 \pi i f}[e^{-2 \pi i f t} |_{T/2}^{+T/2}] $$$$ \mathscr{F} \{g(t)\} = G(f) = \frac{A}{-2 \pi i f}[e^{-\pi f t} - e^{\pi f t}] = \frac{A t}{\pi f t} [\frac{e^{\pi f t} - e^{-\pi f t}}{2 i}]$$$$ \mathscr{F} \{g(t)\} = G(f) = \frac{A t}{\pi f t} sin (\pi f t) = AT [sin (\pi f t)] $$bulunur. Burada sinc fonksiyonu :
$$ sinc(t) = \frac{sin(\pi t)}{\pi t} $$şeklinde tanımlanan bir fonksiyondur.
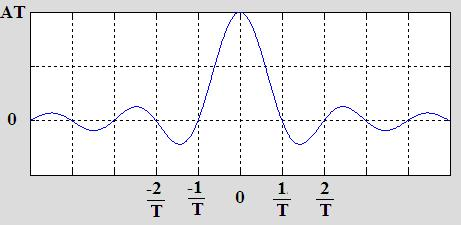
$T = 1$ ve $T = 10$ için Fourier dönüşümleri aşağıdaki gibi elde edilir.
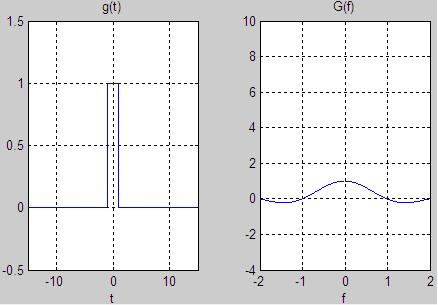
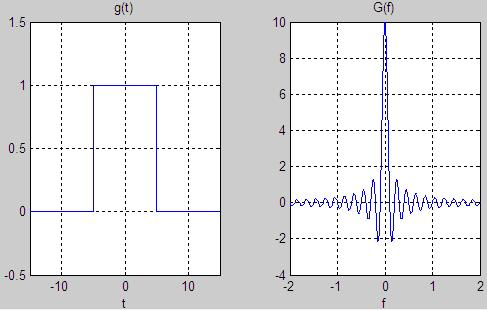
Yukarıdaki iki grafikten yavaş değişen geniş bir kare dalganın, dar bir kare dalgaya göre daha dar Fourier dönüşümüne sahip olduğu görülmektedir. Bu daha yavaş değişen fonksiyonların yüksek frekanslarda daha az enerji içerdiği şeklinde genelleştirilebiilir.
Fourier Dönüşümlerinin Özellikleri¶
Lineerlik: $ \mathscr{F} \{c_1 g(t) + c_2 h(t) \} = c_1 G(f) + c_2 H(f) $
Kaydırma: $ \mathscr{F} \{ g(t-a) \} = e^{-i 2 \pi f a} G(f) $
Ölçeklendirme: $ \mathscr{F} \{ g(ct) \} = \frac{G(f/c)}{|c|} $
Türev: $ \mathscr{F} \{ \frac{dg(t)}{dt} \} = i 2 \pi f G(f) $
Konvolüsyon¶
$f$ ve $g$ fonksiyonlarının konvolüsyonu
$$ f * g (x) := \int_{u=-\infty}^{\infty} f(u) g(x - u) du $$Fonksiyonlar süreksizse:
$$ f * g [n] := \sum_{m=-\infty}^{\infty} f[m] g[n - m] $$şeklinde tanımlanır.
Örnek: Her yerde integrali alınabilir herhangi bir f(x) fonksiyonu ile aşağıdaki şekilde tanımlı bir $a_h(x)$ fonksiyonunun konvolüsyonunu hesaplamaya çalışalım.
$$ a_h(x) := \begin{cases} \frac{1}{2h} & -h \lt x \lt h \\ 0 & \\ \end{cases} $$$$ (f * a_h) (x) = \int_{u=-\infty}^{\infty} f(u) a_h(x - u) du = \frac{1}{2h} \int_{x-h}^{x+h} f(u) du $$Örnek: Dizi Şeklinde Verilen İki Fonksiyonun Konvolüsyonu¶
Süreksiz fonksiyonlar için konvolüsyon tanımını bir liste, dizi ya da küme şeklinde verilen iki süreksiz fonksiyona uygulamak üzere aşağıdaki nümerik örnek verilebilir.
$$ f = (f[0], f[1], f[2], f[3]) := (3, 1, 4, 1) $$$$ g = (g[0], g[1], g[2], g[3]) := (5, 9, 2, 6) $$Tanım uygulanacak olursa;
$ (f * g)[0] = f(0) \times g(0) = 3 \times 5 = 15 $ $ (f * g)[1] = f(0) \times g(1) + f(1).g(0) = 3 \times 9 + 1 \times 5 = 32 $ $ (f * g)[2] = f(0) \times g(2) + f(1).g(1) + f(2).g(0) = 3 \times 2 + 1 \times 9 + 4 \times 5 = 35 $ $ (f * g)[3] = f(0) \times g(3) + f(1).g(2) + f(2).g(1) + f(3).g(0) = 3 \times 6 + 1 \times 2 + 4 \times 9 + 1 \times 5 = 61 $ $ (f * g)[4] = f(1) \times g(3) + f(2) \times g(2) + f(3) \times g(1) = 1 \times 6 + 4 \times 2 + 1 \times 9 = 23 $ $ (f * g)[5] = f(2) \times g(3) + f(3) \times g(2) = 4 \times 6 + 1 \times 2= 26 $ $ (f * g)[6] = f(3) \times g(3) = 1 \times 6 = 6 $
Konvolüsyon Stratejileri:
- Tam Kaydırma: $ f * g = [15, 32, 35, 61, 23, 26, 6] $
- f ve g ile aynı uzunlukta: $ f * g = [32, 35, 61, 23] $
- f ve g’nin bütün elemanlarının kullanıldığı: $ f * g = [61] $
Aynı soruyu farklı konvolüsyon stratejileri lle Python numpy modülü fonksiyonlarından convolve ile çözelim
Öncelikle $g$’nin ters çevrildikten sonra $f$ üzerine baştan sona kadar kaydırıldığı, yani her iki fonksiyonun üstüste geldiği her noktada konvolüsyon işleminin uygulandığı ve sonuç olarak $n+m-1$ (örneğimizde 4 + 4 – 1 = 7) uzunluğunda bir dizi döndüren "full" stratejisini görelim.
import numpy as np
f = np.array([3,1,4,1])
g = np.array([5,9,2,6])
f_konv_g = np.convolve(f,g, mode="full")
print("f*g (full) = ", f_konv_g)
Bu manuel çözüm ile aynıdır. Eğer konvolüsyon işleminin sonuçta, konvolüsyona tabi tutulan her iki fonksiyondan (diziden) uzun olanının uzunluğuna eşit ($max(m,n)$) bir dizi isteniyorsa bu kez "same" stratejisi kullanılır. Konvolüsyon her iki fonksiyonun tamamen örtüştüğü dizi elemanları için uygulanmak isteniyorsa bu kez de "valid" stratejisi kullanılır.
f_konv_g = np.convolve(f,g, mode="same")
print("f*g (same) = ", f_konv_g)
f_konv_g = np.convolve(f,g, mode="valid")
print("f*g (valid) = ", f_konv_g)
Konvoülsyon İşleminde Sınır Belirleme ve Geometrik Anlamı¶
Konvolüsyon işleminde integralin sınırlarını belirleme konusu önemli bir konudur. Aşağıdaki örneği bu amaçla inceleyelim.
$$ f(x) := \begin{cases} 1 & 0 \lt x \lt 1 \\ 0 & \\ \end{cases} $$ve
$$ g(x) := \begin{cases} x & 0 \lt x \lt 2 \\ 0 & \\ \end{cases} $$olsun.
Böyle bir durumda integrasyon sınırları belirlenirken her iki fonksiyonunun sınırlarını dikkate almak gerekir. Örneğimizde sınırlar aşağıdaki şekilde belirlenmiştir.
$$ \int_{0 \lt x \lt 1, 0 \lt x - u \lt 2} f(u) g(x - u) du = \int_{min(1,max(0,x-2))}^{max(0,min(1,x))} (x-u) du $$İntegrasyon sınırlarını ve parçalı fonksiyon olarak tanımlanmış fonksiyonlar için bu sınırlar arasında hangi ifadenin geçerli olduğunu belirlemek üzere daha iyi bir yöntem $f(t)$ ve g(x-t)$ fonksiyonlarının birer grafiğini çizip aşağıdaki işlemleri uygulamaktır.
1) Katlama (ing. folding): g(u) fonksiyonunun y eksenine göre simetriği alınır (g(-u))
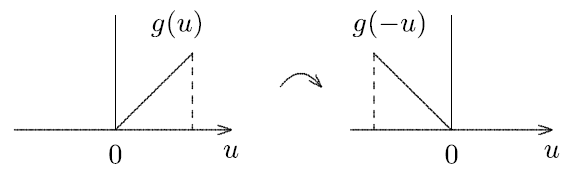
2) Kaydırma (ing. displacement): g(-u) fonksiyonu x ekseninde x kadar kaydırılır (g(x-u))
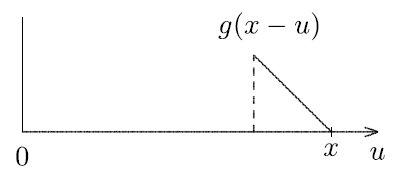
2) Çarpma (ing. multiplication): f(u) ile g(x-u) fonksiyonu çarpılır (f(u).g(x-u))
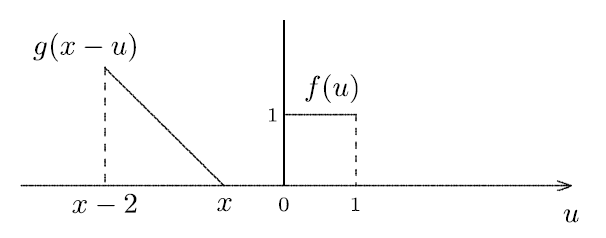
4) İntegrasyon (ing. integration): Bu işlem bütün x’ler için yapılarak f(u) ve g(x-u) altında kalan ortak alan hesaplanır.
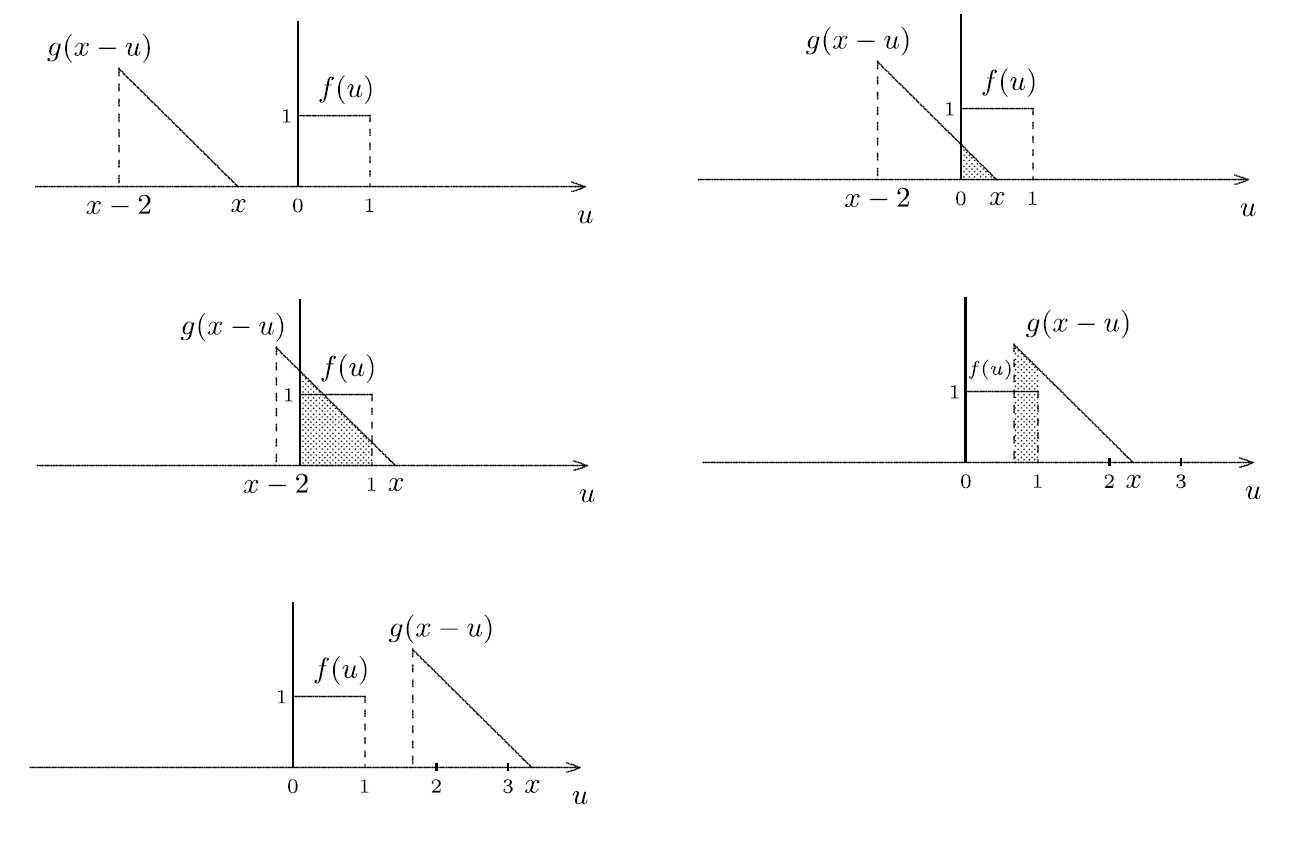
Sonuç olarak
$$ (f*g) (x) = \frac{1}{2} \begin{cases} x^2 & 0 \le x \le 1 \\ 2x-1 & 1 \le x \le 2 \\ -x^2 + 2x + 3 & 2 \le x \le 3 \\ 0 & \\ \end{cases} $$konvolüsyonu elde edilmiş olur.
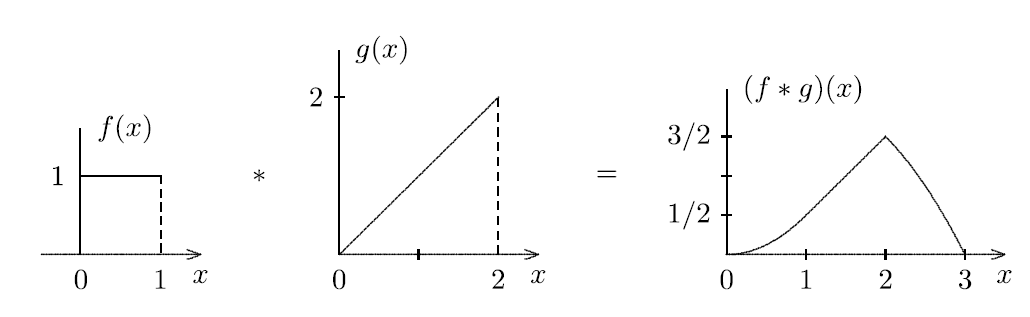
Astronomide genellikle gözlem penceresi fonksiyonu (ing. window function) delta fonksiyonları ile verildiğinden bir $\delta$-fonksiyonunun herhangi başka bir fonksiyonla (sinyal, s(t)) konvolüsyonuna değinmekte fayda vardır.
$$ y(t) = s(t) * \sum_{k = -\infty}^{+\infty} \delta (t - k \Delta t) $$ $$ \sum_{k = -\infty}^{+\infty} s(t) \delta (t - k \Delta t) = \sum_{k = -\infty}^{+\infty} s(t - k \Delta t) $$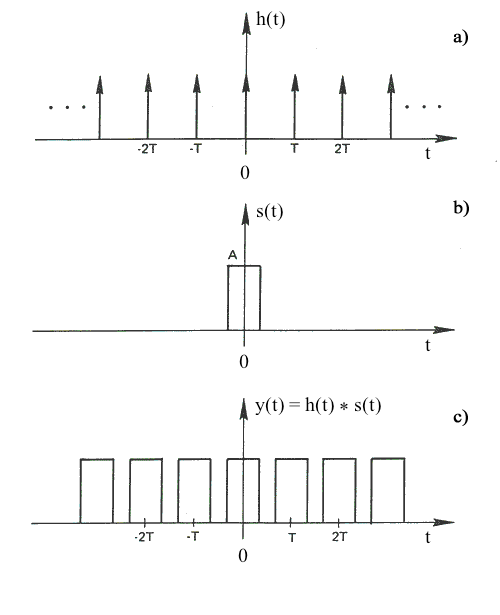
Konvolüsyon Teoremi¶
$f(t)$ ve $g(t)$ fonksiyonlarının Fourier dönüşümleri aşağıdaki şekilde tanımlanmak üzere,
$$ \mathscr{F} \{f(t)\} = F(f) = \int_{-\infty}^{+\infty} f(t) e^{-2 \pi f t} dt $$ $$ \mathscr{F} \{g(t)\} = G(f) = \int_{-\infty}^{+\infty} g(t) e^{-2 \pi f t} dt $$$h(z)$, $f(t)$ ile $g(t)$'nin konvolüsyonu, $H(f)$ de bu konvolüsyonun Fourier dönüşümü olsun.
$$ h(z) = \int_{-\infty}^{+\infty} f(t) g(z - t) dt $$$$ \mathscr{F} \{h(z)\} = H(f) = \int_{-\infty}^{+\infty} h(t) e^{-2 \pi f t} dt $$$$ \mathscr{F} \{h(z)\} = H(f) = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(t) g(z - t) dt e^{-2 \pi f t} dt $$olur. Bu durumda,
$$ H(f) = \int_{-\infty}^{+\infty} f(t) (\int_{-\infty}^{+\infty} g(z - t) e^{-2 \pi f t} dt) dt $$$y = z - t$ ve dy = dz değişken değiştirmesi uygulanacak olursa;
$$ H(f) = \int_{-\infty}^{+\infty} f(t) (\int_{-\infty}^{+\infty} g(y) e^{-2 \pi f (y+t)} dy) dt $$$$ H(f) = \int_{-\infty}^{+\infty} f(t) e^{-2 \pi f t} (\int_{-\infty}^{+\infty} g(y) e^{-2 \pi f y} dy) dt $$$$ H(f) = (\int_{-\infty}^{+\infty} f(t) e^{-2 \pi f t} dt) (\int_{-\infty}^{+\infty} (g(y) e^{-2 \pi f y} dy) $$olur. Sonuç olarak
$$ H(f) = F(f) G(f) $$elde edilmiştir. Yani, iki fonksiyonun konvolüsyonlarının Fourier dönüşümü, her bir fonksiyonun Fourier dönüşümlerinin çarpımıdır.
Aynı şekilde iki fonksiyonun çarpımlarının Fourier dönüşümü de fonksiyonların Fourier dönüşümlerinin konvolüsyonuna eşittir!
Yani fonksiyonların çarpımı ile dönüşümlerinin konvolüsyonu bir Fourier çifti teşkil eder. Bu özdeşliğe konvolüsyon teoremi denir.
$$ f(t) g(t) \Longleftrightarrow F(f) G(f) $$Korelasyon¶
Korelasyon da konvolüsyona çok benzer tanımlanır ve katlama dışında ($u \Rightarrow -u$) aynı işlem gibi görünür. Zira kaydırma, çarpma ve integrasyon aynı şekilde uygulanır. Hatta $f(-u) = f(u)$ şartını sağlayan (çift) reel fonksiyonlar için korelasyon ve konvolüsyon aynı şeydir. $f(u)$ kompleks bir fonksiyon olduğunda onun eşleniği ($\bar{f(u)}$) integrasyon işlemine girer.
$$ f \star g := \int_{u=-\infty}^{+\infty} \bar{f(u)} g(u + t) du $$Fonksiyonlar süreksizse tanım benzerdir.
$$ f \star g := \sum_{m=-\infty}^{+\infty} \bar{f[m]} g[m + n] $$Korelasyon ifadesinde $f$ ve $g$ fonksiyonları birbirinden farklı fonksiyonlar ise işleme çapraz korelasyon (ing. cross correlation), işlem aynı fonksiyonlar arasında ise bu kez otokorelasyon (ing. autocorrelation) adını alır.
Çapraz korelasyonlar iki fonksiyon arasındaki benzerliği belirlemek için kullanılır. Çapraz korelasyonla bir fonksiyonun x (ya da zaman) ekseninde ne kadar kaydırıldığında diğerine “benziyor” olduğu belirlenir. Sinyal işlemede bir sinyallin diğerine göre ne kadar geciktiği (ing. time lag) ya da spektroskopide bir tayfın referans bir tayfa göre dalgaboyu ekseninde ne kadar kaydığı (ing. Doppler shift) gibi benzerlikler çapraz korelasyon fonksiyonları ile araştırılır.
$$ f(t) \star g(t) = f(-t) \star g(t) = f(t) \star g*(-t) $$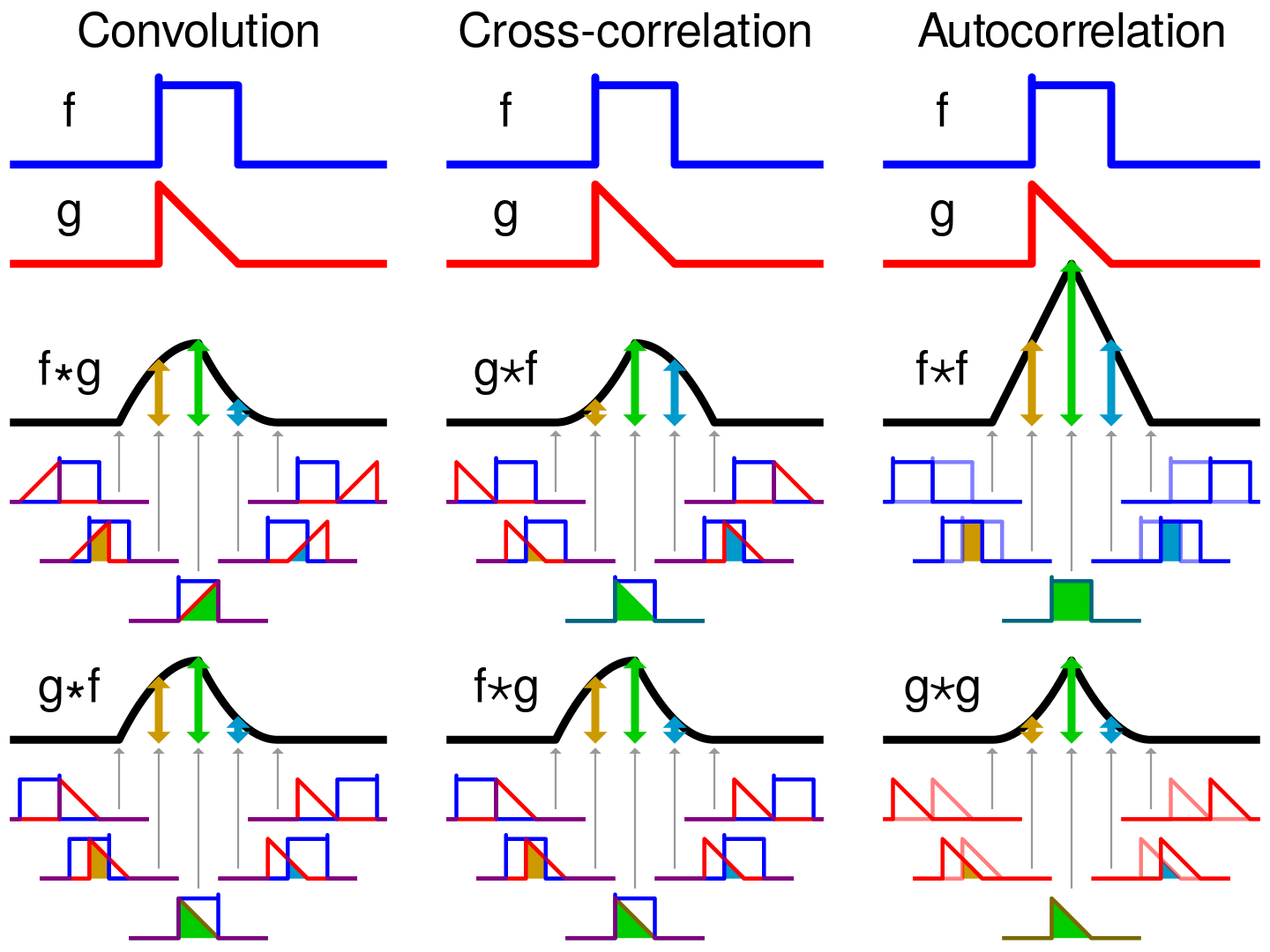
Korelasyon Teoremi¶
$F(f)$ ve $G(f)$ sırasıyla $f(t)$ ve $g(t)$ fonksiyonlarının Fourier dönüşümleri olmak üzere;
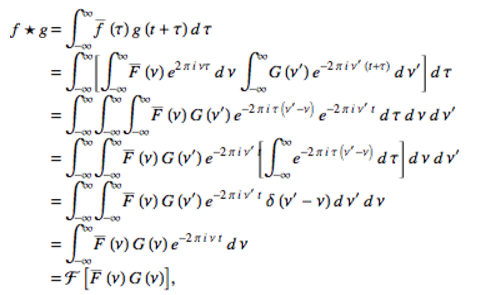
Yani $f$ ve $g$ fonksiyonlarının çapraz korelasyonu bu fonksiyonların Fourier dönüşümlerinin çarpımının Fourier dönüşümüne eşittir.
Wiener Khinchin Teoremi¶
$C(t) = \int_{\tau=-\infty}^{+\infty} \bar{E(t)} E(\tau + t) d\tau $ şeklinde tanımlanan otokorelasyon fonksiyonunun Fourier dönüşümü
$$ \mathscr{F} \{E\} = E(\nu) = \int_{-\infty}^{+\infty} E(\nu) e^{-2 i \pi \nu \tau} d\nu $$ve onun kompleks eşleniği
$$ \mathscr{F} \{\bar{E}\} = \bar{E(\nu)} = \int_{-\infty}^{+\infty} \bar{E(\nu)} e^{2 i \pi \nu \tau} d\nu $$olmak üzere
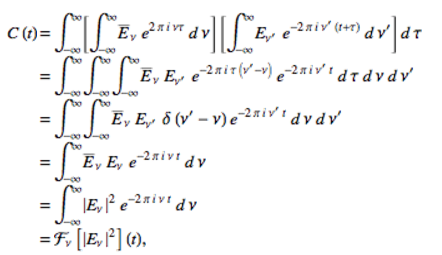
Perseval Teoremi¶
Görüldüğü üzere bir fonksiyon için tanımlanan otokorelasyon fonksiyonu ile onun Fourier dönüşümü aynı enerjiye ($E^2(\tau) \Rightarrow E^2(\nu)$) sahiptir. Bu özellik Parseval teoremi ile ifade olunur.
Python’da korelasyon konvolüsyona çok benzer şekilde bu kez numpy.correlate fonksiyonu kullanılarak yapılır. Doğası gereği bu işlemin farkı ikinci fonksiyonun “katlanmamasıdır” (y-ekseninde simetriği alınmaz.
Tıpkı konvolüsyonda olduğu gibi "full" (varsayılan), "same" ve "valid" stratejileriyle çapraz ve otokorelasyon yapılabilir.
import numpy as np
f = np.array([3,1,4,1])
g = np.array([5,9,2,6])
f_corr_g = np.correlate(f,g, mode="full")
print("f corr g (full) = ", f_corr_g)
f_corr_g = np.correlate(f,g, mode="same")
print("f corr g (same) = ", f_corr_g)
f_corr_g = np.correlate(f,g, mode="valid")
print("f corr g (valid) = ", f_corr_g)
f_corr_f = np.correlate(f,f, mode="full")
print("f corr f (full autocorrelation) = ", f_corr_f)
g_corr_g = np.correlate(g,g, mode="full")
print("g corr g (full autocorrelation) = ", g_corr_g)
Örneklendirme Teoremi¶
Sınırlı (ing. band-limited) bir sinyallin gözlemler sonucu tekrar aynen oluşturulabilmesi (ing. reconstruction) için içerdiği maksimum frekansın en az iki katı frekansta örneklenmesi gerekir.
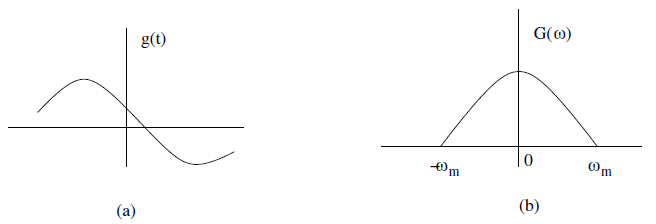
Yukarıda kendisini ve Fourier dönüşümünü gördüğünüz sinyalin frekansı $\omega_m$ olsun. Bu sinyalin gözlemlerle aynen elde edilebilmesi (gözlem noktaları kullanılarak sinyallin oluşturulabilmesi)için $f_s \gt 2 \omega_m$ ‘lik bir frekansta gözlem noktası alınması gerekir. İhtiyaç duyulan bu minimum frekansa ($2 \omega_m$) Nyquist frekansı adı verilir.
$\delta_T(t)$ fonksiyonu örneklendirme fonksiyonu (ing. sampling function), $\delta_T(\omega)$ ise frekans örneklendirme fonksiyonu (ing. frequency sampling function) adını alır.
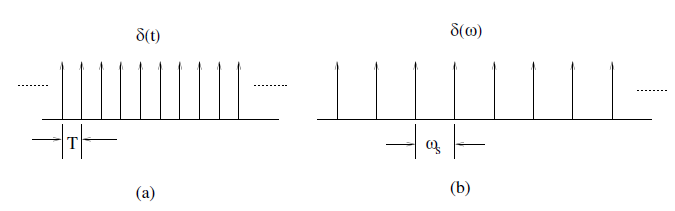
Bu durumda sinyalin Fourier dönüşümü aşağıdaki şekilde elde edilir.
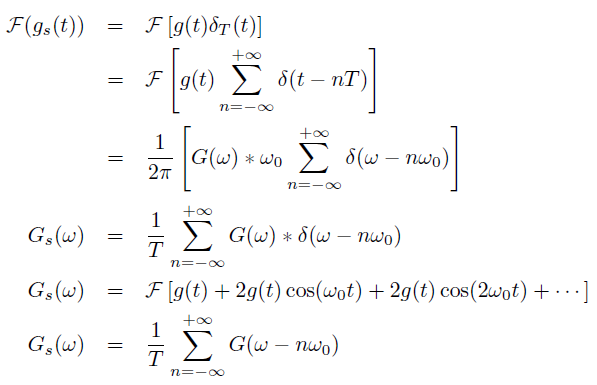
Gözlem frekansı $\omega_s \ge 2 \omega_m$ ise ($T = \frac{1}{2} f_m$) bu sinyal tekrar oluşturulabilir.
Gözlem penceresinin ($H_{2\omega}$) (ing. spectral window) en az $2\omega_m$ büyüklüğünde olması gerekir ki sinyal yeniden oluşturulabilsin. Gözlem penceresinin zaman tanım kümesindeki karşılığı pencere fonksiyonu (ing. window function) adını alır.
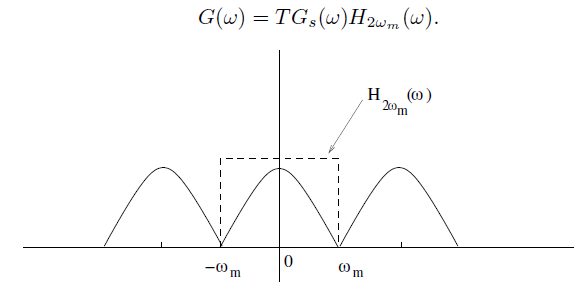
Örnek 1¶
1 Hz frekansa sahip aşağıdaki sinyali ele alalım.
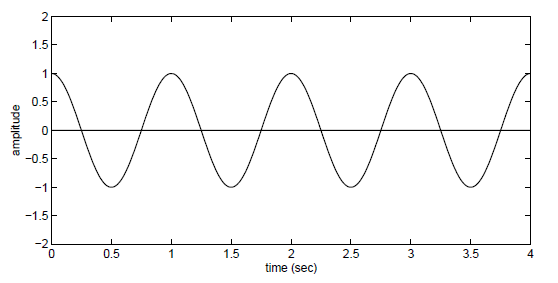
Sinyali 2 Hz frekansla örneklersek tekrar oluşturmamız mümkün olur.
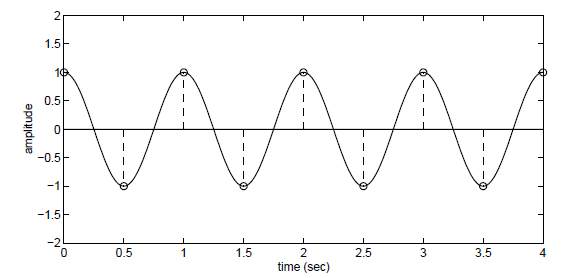
Sinyali 3 Hz frekansla örneklersek orjinal sinyali oluşturmamız daha da kolay olur. (ing. oversampling)
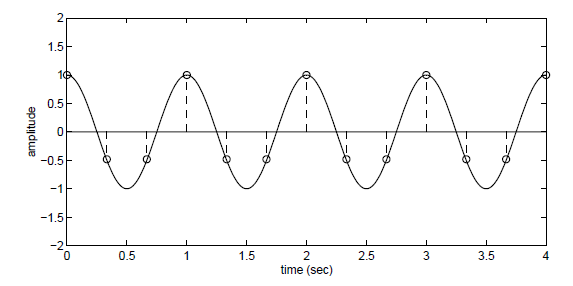
Ancak sinyali 1.5 Hz frekansla örneklersek tekrar oluşturmamız mümkün olmaz (ing. undersampling). Sadece bilgi kaybetmemiş aynı zamanda bu sinyal hakkında yanlış bir izlenim de edinmiş oluruz. Aşağıda bu frekansla yapılan örneklendirmeden yeniden oluşturulmuş sinyali görüyorsunuz.
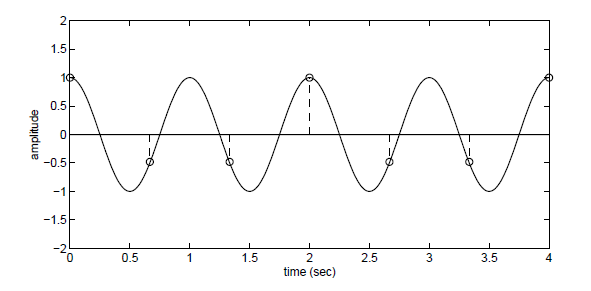
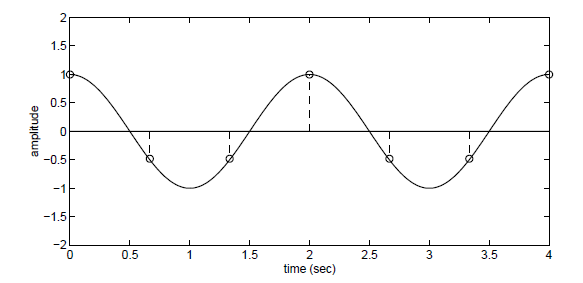
Yüksek frekans içeriğinin gözlenememesi durumuna neden olan frekans örtüşmesi olgusuyla astronomide, özel olarak da yüksek frekanslı değişimlerin gözlenebildiği asterosismoloji gibi alanlarda sıklıkla karşılaşılır.
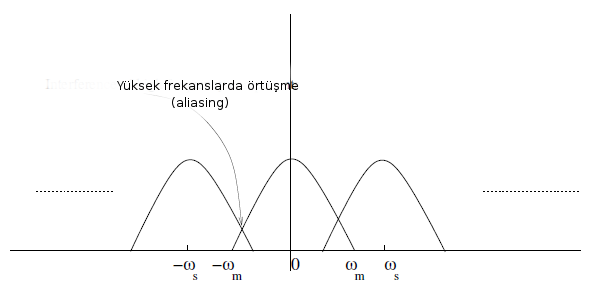
Gözlemlerin sinyalin içerdiği maksimum frekanstan daha yüksek bir frekansla gerçekleşmesi durumunda Fourier tanım kümesinde frekans piklerinin birbirinden iyice ayrıldığı ve bu nedenle sinyalin gözlenen frekanstan tekrar oluşturulabileceği görülür. Nyquist frekansının üstünde gözlem yapılan duruma ing. oversampling adı verilir.
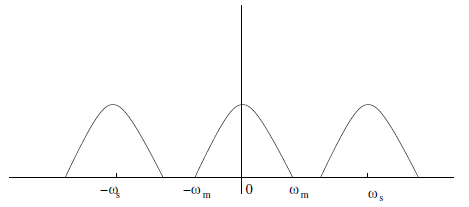
Örnek 2¶
Çoğul frekansların varlığı durumunda verinin orjinal sinyalin içerdiği en yüksek frekansın iki katı frekansta alınması gerekir.
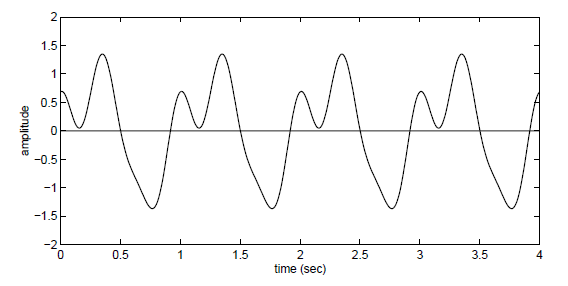
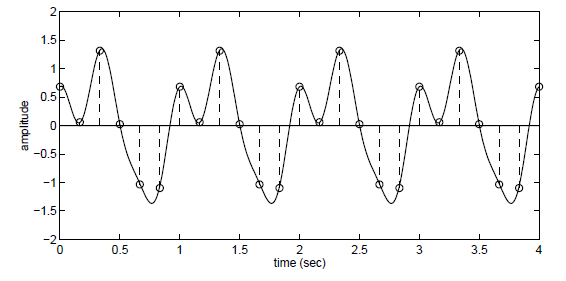
Bu örnekteki en yüksek frekans 3 Hz olup, 6 Hz frekansla örneklersek tekrar oluşturabiliriz.
Süreksiz Fourier Dönüşümü¶
Fourier dönüşümlerinin sürekli fonksiyonlara nasıl uygulandığını gördük ancak gerçekte sürekli fonksiyonlar yerine süreksiz (ing. discontinous),ve belirli bir gözlem penceresi içinde yer alan (ing. band-limited) veriyle karşılaşılır. Bu durumda süreksiz Fourier dönüşümlerine başvurulur.
$$ \int_{-\infty}^{+\infty} f(t) e^{2 \pi i f t} dt \Rightarrow F_n = \sum_{k=0}^{N-1} f_k e^{2 \pi i n k/N} $$Bu durumda ters süreksiz Fourier dönüşümü (ing. Inverse Discrete Fourier Transform)
$$ f_k = \mathscr{F}_n^{-1} [\{F_n\}_{n=0}{N-1}](k) \Rightarrow f_k = \frac{1}{N} \sum_{n=0}^{N-1} F_n e^{2 \pi i n k/N} $$Yukarıdaki dönüşümün bir sonucu olarak periyodik bir fonksiyonun Fourier dönüşümünde sadece periyodun karşılık geldiği frekansta bir pik yerine, bir pik de o frekansın negatif değerinde oluşur.
$$ n = 0 - \omega_0 , 1 \le n \le N/2 - 1 \Rightarrow 0 < \omega < \omega_c , N/2 + 1 \le n \le N - 1 \Rightarrow -\omega_c < \omega < 0 \Rightarrow N = N/2 \Rightarrow \omega = \pm \omega_c $$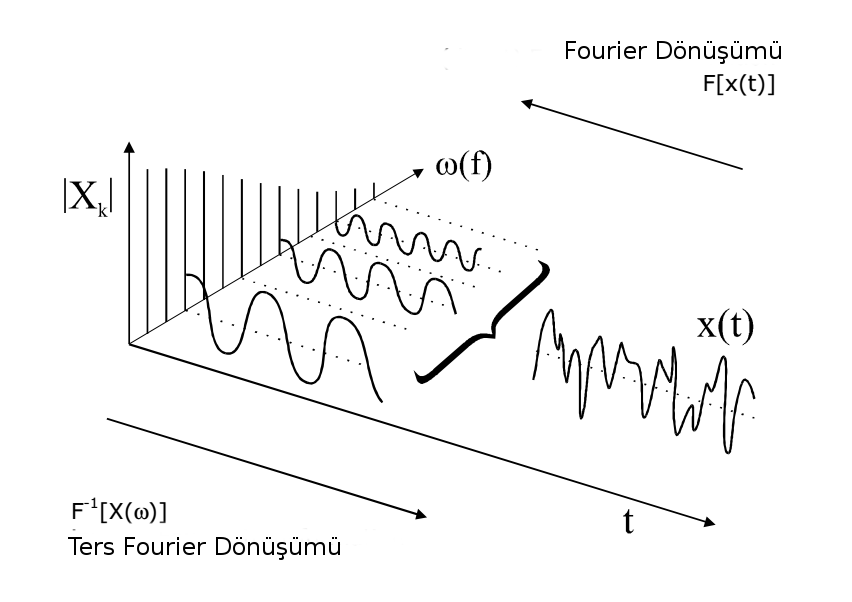
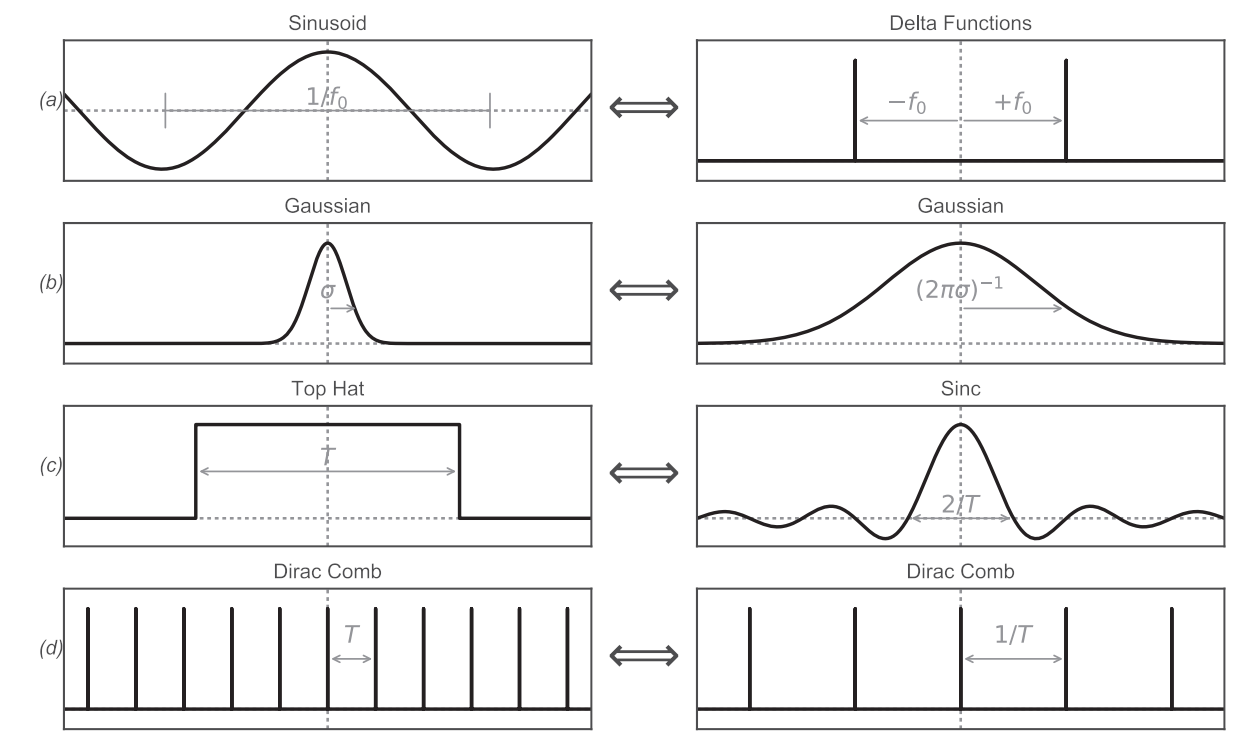
Astronomi Açısından Önemli Bazı Fonksiyonların Fourier Dönüşümü¶
Hızlı Fourier Dönüşümü¶
Süreksiz Fourier dönüşümünde $f_k$’nın $e^{-2 \pi i k n / N}$ terimi ile $N$ kez çarpımı (ki bu çarpımların hepsi kompleks uzayda yapılır) ve elde edilen değerlerin $N$ kez toplamı gerekir (işlemin karmaşıklığı $N^2$ ile orantılıdır). Bu nedenle "Yavaş" Fourier Dönüşümü olarak da adlandırılır. Hızlı Fourier Dönüşümleri Fourier dönüşümlerinin simetri gibi bazı özelliklerinden faydalanarak bu karmaşıklığı $N log_2 N$ düzeyine indirir.
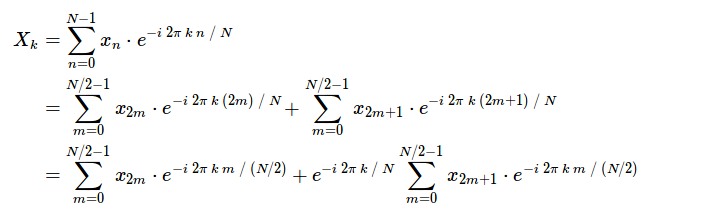
Cooley – Tukey algoritmasında olduğu gibi dönüşüm tek ve çift bileşenlerine ayrıldıktan sonra her bir bileşenin de içinde simetrik olduğu görülür. Bu simetri sinyalin yapısına da bağlı olarak daha fazla basitleştirme de getirir ve DFT matrisinin pek çok elemanı 0 olur. Bu elemanlarla çarpma yapmak anlamlı olmayacağı için hiç işlem yapılmaz. Bu noktada FFT’nin yapısı gereği $N$’in 2’nin kuvvetleri olması durumunda çalışacağını, aksi takdirde ya atma (ing. truncation) ya da 0’la doldurma (ing. zero padding) yapılması gerektiğini vurgulamak gerekir.
# Yavas Fourier Donusumu
import numpy as np
def DFT_slow(x):
"""x 1D dizisinin sureksiz Fourier donusumu
"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
n = np.arange(N)
k = n.reshape((N, 1))
M = np.exp(-2j * np.pi * k * n / N)
return np.dot(M, x)
# Hizli Fourier Donusumu
def FFT(x):
"""
1D Cooley-Tukey FFT
"""
x = np.asarray(x, dtype=float)
N = x.shape[0]
if N % 2 > 0:
raise ValueError("x 2nin kuvveti olmali")
elif N <= 32: # N yeterince kucukse yavas algoritma
return DFT_slow(x)
else:
X_cift = FFT(x[::2])
X_tek = FFT(x[1::2])
carpan = np.exp(-2j * np.pi * np.arange(N) / N)
return np.concatenate([X_cift + carpan[:N / 2] * X_tek,\
X_cift + carpan[N / 2:] * X_tek])
Spektral Yoğunluk ve Güç Spektrumu¶
Tüm fiziksel sinyaller sürekli ve süreksiz Fourier dönüşümü yoluyla içerdiği frekans bileşenlerine ayrıştırlabilir. Bir sinyalin spektral enerji dağılımı sinyaldeki toplam enerjinin tüm frekanslara dağılımıdır. Bir sinyalin her frekansta sahip olduğu enerji ise spektral güç yoğunluğu (ing. the power spectral density (PSD)) olarak adlandırılır. Frekans analizinde geenellikle sinyalin her frekanstaki genliği yerine, her bir frekanstaki güç yoğunluğunun incelenmesi tercih edilir. Sinyalin toplam gücü,
$$ E = \int_{-\infty}{+\infty} |x(t)|^2 dt $$ve Perseval teoremi gereğince,
$$ \int_{-\infty}{+\infty} |x(t)|^2 dt = \int_{-\infty}{+\infty} |x(f)|^2 df $$şeklinde verilir. Bir başka deyişle sinyal ile onun Fourier dönüşümü aynı enerjiyi içerir.
Genlik yerine genellikle güç yoğunluğunun tercih edilmesinin nedeni, Fourier dönüşümlerinde genliğinin karesinin hem kompleks bileşenlerden kurtulunmasına, hem de evre kaymalarının elenmesine olanak sağlamasıdır. Sinyaldei $t_0$ kadarlık bir gecikme için Fourier dönüşümü
$$ \mathscr{F} \{g(t - t_0)\} = \mathscr{F} \{g(t)\} e^{-2 \pi i f t} $$olduğu ve güç
$$ \mathscr{P}_g \equiv |\mathscr{F}\{g\}|^2 $$şeklinde tanımlandığı için hem evre seçimi, hem de kompleks bileşenler problem olmaktan çıkar. $|x(f)|^2$ , sinyalin $f$ frekansında sahip olduğu gücü, yani frekans başına enerjiyi tarif ettiği için bir yoğunluk fonksiyonu olarak düşünülebilir. Dolayısı ile sinyalin her bir frekanstaki genliğinin karesi, spektral güç yoğunluğu ya da daha sık kullanılan deyimiyle güç spektrumu (ing. power spectrum) olarak adlandırılır. Güç spektrumu böylece her bir frekansın toplam sinyale katkısını belirleyen pozitif ve reel bir fonksiyon olarak tanımlanmış olur.
Klasik Periyodogram¶
Sonuç olarak klasik periyodogram (Schuster periyodogramı) fonksiyonla süreksiz Fourier dönüşümünün toplamda aynı güce sahip olması için gücünün nokta sayısına ($N$) normalize edilmesiyle elde edilir ve $x(t)$ zaman serisine karşılık gelen $X(\nu)$ frekanslarından her birinin ne kadar güce sahip olduğunu $P_N(\nu)$ ifade eder.
$$ P_N (\nu) = \frac{1}{N} |F_N (\nu)|^2 = \frac{1}{N} | \sum_{i=1}{N} x(t_i) e^{2 \pi i \nu t_i} |^2 $$$$ P_N (\nu) = \frac{1}{N} \{ (\sum_{i=1}{N} x(t_i) sin(2 \pi \nu t_i) |^2 ) + (\sum_{i=1}{N} x(t_i) cos(2 \pi \nu t_i) |^2 ) \} $$$x(t)$ sinyali $x(t_i) = A cos(2 \pi \nu_1 t_i) $ şeklinde bir sinüsoidalse periyodogramın $\nu_1$ frekansında değeri
$$ P_N (\nu_1) = \frac{1}{N} \{ (\sum_{i=1}{N} A cos(2 \pi \nu_1 t_i) sin(2 \pi \nu_1 t_i) \}^2 + \{ \sum_{i=1}{N} A cos^2(2 \pi \nu_1 t_i) \}^2 $$$N$ yeterince büyükse (çok sayıda veri noktası varsa, $N \rightarrow \infty$)
$$ \sum_{i=1}{N} cos(2 \pi \nu_1 t_i) sin(2 \pi \nu_1 t_i) \sim 0 , \sum_{i=1}{N} cos^2(2 \pi \nu_1 t_i) \sim N/2 $$olur.
scipy.signal.periodogram herhangi bir $x(t)$ zaman serisi için spektral güç yoğunluğunu bir periyodogramla verir. Zaman serisi veri $x$ ’in örnekleme frekansı fs, gözlem penceresi (spectral window) window parametreleriyle sağlanır. İstendiği takdirde hızlı Fourier dönüşümünün uzunluğu (nfft), kompleks sinyaller yerine gerçek sinyaller söz konusu olduğunda tek taraflı güç spektrumu (return_onesided) istenirse yoğunluk ($\nu^2$ / Hz, karekökü doğrudan genliği verecek şekilde ölçeklendirilmiş) istenirse de $\nu$ biriminde (scaling) bir periyodogram alınır. Örnek olarak önce sentetik bir veri üretip sonra onu analiz edelim.
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# Sentetik bir sinyal yaratip uzerine gurultu ekleyelim.
fs = 1e4 # ornekleme frekansi (veri alinma sikligi)
N = 1e5 # nokta sayisi
A = 2*np.sqrt(2) # degisim genligi
v = 1234.0 # degisim frekansi
gurultu = 0.001 * fs / 2 # sentetik gurultu (beyaz)
t = np.arange(N) / fs # zaman
x = A*np.sin(2*np.pi*v*t) # x sentetik sinyali
plt.plot(t,x,'r-')
# sinyale gurultu ekleyelim
x += np.random.normal(scale=np.sqrt(gurultu), size=t.shape)
# sinyali cizdirelim
plt.plot(t,x,'b+')
plt.xlabel("t (saniye)")
plt.ylabel("x(t)")
plt.show()
Kolay gösterim için veri noktası sayısı N = 1000 ile sınırlandırılırsa
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# Sentetik bir sinyal yaratip uzerine gurultu ekleyelim.
fs = 1e4 # ornekleme frekansi (veri alinma sikligi)
N = 1e3 # nokta sayisi
A = 2*np.sqrt(2) # degisim genligi
v = 1234.0 # degisim frekansi
gurultu = 0.001 * fs / 2 # sentetik gurultu (beyaz)
t = np.arange(N) / fs # zaman
x = A*np.sin(2*np.pi*v*t) # x sentetik sinyali
plt.plot(t,x,'r-')
# sinyale gurultu ekleyelim
x += np.random.normal(scale=np.sqrt(gurultu), size=t.shape)
# sinyali cizdirelim
plt.plot(t,x,'b+')
plt.xlabel("t (saniye)")
plt.ylabel("x(t)")
plt.show()
scipy.signal.periodogram örneklemenin yapıldığı frekansları ve bu frekanslardaki spektral güç yoğunluğunu (periyodogramı) verir. Aşağıdaki kod parçasıyla bu parametreleri alıp çizdirelim. Yalnız numpy.random.normal fonksiyonuyla ortalaması 0, standart sapması 1 olan bir normal dağılımdan rastgele çektiğimiz noktalarla kendi yarattığmız gürültünün frekans uzayındaki karşılığını göstermek üzere y-eksenini logaritmik çizdirelim (plt.semilogy). İsterseniz plt.plot ile lineer çizdirmeyi deneyebilirsiniz. Ayrıca gürültünün seviyesini de hesaplayıp, ekrana getirelim.
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
# Sentetik bir sinyal yaratip uzerine gurultu ekleyelim.
fs = 1e4 # ornekleme frekansi (veri alinma sikligi)
N = 1e5 # nokta sayisi
A = 2*np.sqrt(2) # degisim genligi
v = 1234.0 # degisim frekansi
gurultu = 0.001 * fs / 2 # sentetik gurultu (beyaz)
t = np.arange(N) / fs # zaman
x = A*np.sin(2*np.pi*v*t) # x sentetik sinyali
#sinyalin kendisini cizdirirken N = 1e3 aliniz
#plt.plot(t,x,'r-')
# sinyale gurultu ekleyelim
x += np.random.normal(scale=np.sqrt(gurultu), size=t.shape)
# sinyali cizdirelim
plt.plot(t,x,'b+')
plt.xlabel("t (saniye)")
plt.ylabel("x(t)")
plt.show()
# frekanslari ve her bir frekanstaki spektral guc yogunlugunu
# periodogram fonksiyonunda alalim
frekans, guc_yogunlugu = signal.periodogram(x, fs, scaling='density')
plt.semilogy(frekans, guc_yogunlugu)
plt.xlabel('Frekans [Hz]')
plt.ylabel('PSD [v**2 / Hz]')
plt.show()
# Gurultu seviyesi
gurultu_f = np.mean(guc_yogunlugu[256:])
print("Beyaz gurultu seviyesi: ", gurultu_f)
# Guc spektrumu
frekans, guc_spektrumu = signal.periodogram(x, fs, scaling='spectrum')
plt.semilogy(frekans, guc_spektrumu)
plt.xlabel('Frekans [Hz]')
plt.ylabel('Guc [v**2]')
plt.show()
pik_frekans = frekans[guc_spektrumu.argmax()]
pik_genlik = np.sqrt(guc_spektrumu.max())
df = guc_spektrumu[1] - guc_spektrumu[0]
pik_genlik_hatasi = np.sqrt(np.sum(guc_spektrumu*df))
print("Pikin maksimumu {:.4f} Hz'te ve genligi {:.4f} +\- {:.4f}".\
format(pik_frekans, pik_genlik, pik_genlik_hatasi))
# Genlik spektrumu (sqrt(guc_spektrumu))
plt.semilogy(frekans, np.sqrt(guc_spektrumu))
plt.xlabel('Frekans [Hz]')
plt.ylabel('Genlik [sinyalle ayni birimde (v)]')
plt.axvline(x=pik_frekans, c='r', ls="--")
plt.axhline(y=pik_genlik, c='g', ls="--")
plt.show()
Yukarıdaki kodla 1234 Hz frekanslı bir sinüs üzerinden kendi ürettiğimiz ve analiz etmek istediğimiz sentetik verinin spektral güç yoğunluğu diyagramı (periyodogramı). Y-ekseninde spektral güç yoğunluğu bulunmaktadır. Gördüğünüz gibi 1234 Hz. piki periyodogramda açıkça görünmektedir. Gürültünün gücü ortalama 0.0018’dir. Ortalama gürültü hesabı için kodda guc_yogunlugu dizisinin frekans pikinin bulunduğu frekanstan sonraki indeksleri almak üzere $[256:]$ dilimlemesi yapılmıştır.
İstendiği takdirde spektral güç yoğunluğu yerine güç spektrumu (ing. power spectrum) adı verilen, genliğin karesiyle ölçekli spektral güç scaling parametresi spectrum değerine atanarak çizdirilebilir. Bu durumda y-ekseninde genliğin karesiyle ölçeklendirilmiş güç parametresi bulunur. Eksenin yine logaritmik olduğuna dikkat ediniz.
Genlik Spektrumu¶
$\nu \neq \nu_1$ frekanslarında hem $x(t_i) sin (2 \pi \nu_1 t_i)$ terimleri, hem de $x(t_i) cos (2 \pi \nu_1 t_i)$ terimlerinde negatif ve pozitif terimler oluşur ve toplamda bu terimler birbirlerini büyük ölçüde sadeleştirdiği için toplam küçük olur. Yani verinin içindeki $\nu_1$ frekansı dışındaki test frekanslarında $P_N$ değeri küçük olur.
$P_N(\nu)$ maksimum değerini verinin içindeki frekansta alır. 100 civarında nokta sayısından itibaren $P_N \sim A^2 N / 4$ gayet iyi bir yaklaşım haline gelir. Bu nedenle genliğin değerini direkt periyodogramdan görmek amacıyla frekansa karşılık
$$ A(\nu) = \sqrt{\frac{4 P_N(\nu)}{N}} $$grafiği çizilir. Böylece her bir frekanstaki değişimin genliği direkt grafik üzerinden okunmuş olur. Bu şekilde oluşturulan periyodograma genlik periyodogramı ya da genlik spektrumu (ing. amplitude spectrum) adı verilir.
Sonuç olarak amacımız her bir değişim modunun genliğini belirlemek ve bu bilgiyi yorumlamaktır. Bu noktada dikkat çekilmesi gereken bir husus bilgisayar kodları ya da paket programlar aracılığyla kullanılan periyodogramlarda elde edilen güç spektrumlarının ne şekilde ölçeklendiğidir. Örneğin scipy.signal.periodogram ekseni $P_N(\nu)^2 / N$ ile ölçeklendirir. Dolayısı ile yarı-genlik için verilen dizinin karekökünü almak yeterli olur.
Maksimum gücün olduğu frekanstaki genlik, güç spektrumunun o frekans için değerinin kareköküyle elde edilir. Pikin maksimumu 1234.00 Hz'te bullunmuştur ve genligi 2.0161’dır. Orjinall sinyalimizin yarı-genliği $2 \sqrt{2} \sim 2.83$ idi ancak biz onun üzerine gürültü de eklemiştik. Gürültü barındıran verinin içindeki sinyalin genliğini belirlerken hata olması normaldir. Bu hatanın düzeyi $RMS = \sqrt{\Sigma(PSD \times df)} = 0.0278$ ile verilir. Burada $df$: tayfsal çözünürlük olup, iki nokta arasındaki frekans biriminden uzaklıktır. Sinyal üzerindeki gürültüyü rastgele ürettiğimizden bu değerler sizin için farklı olabilir.
Düzensiz Aralıklı Yapılan Gözlemler ve Nyquist Limiti¶
İdeal durumdan farklı olarak gözlemlerde belirli bir zaman aralığı dahilinde sonlu poz süreleriyle ve gece / gündüz, mevsim değişimi gibi nedenlerle değişen aralıklarda gözlem yapılır. Bu nedenle periyodogram alttaki gerçek sinyalin değil, sinyal ile gözlem penceresinin bir konvolüsyonu olarak düşünülmelidir.
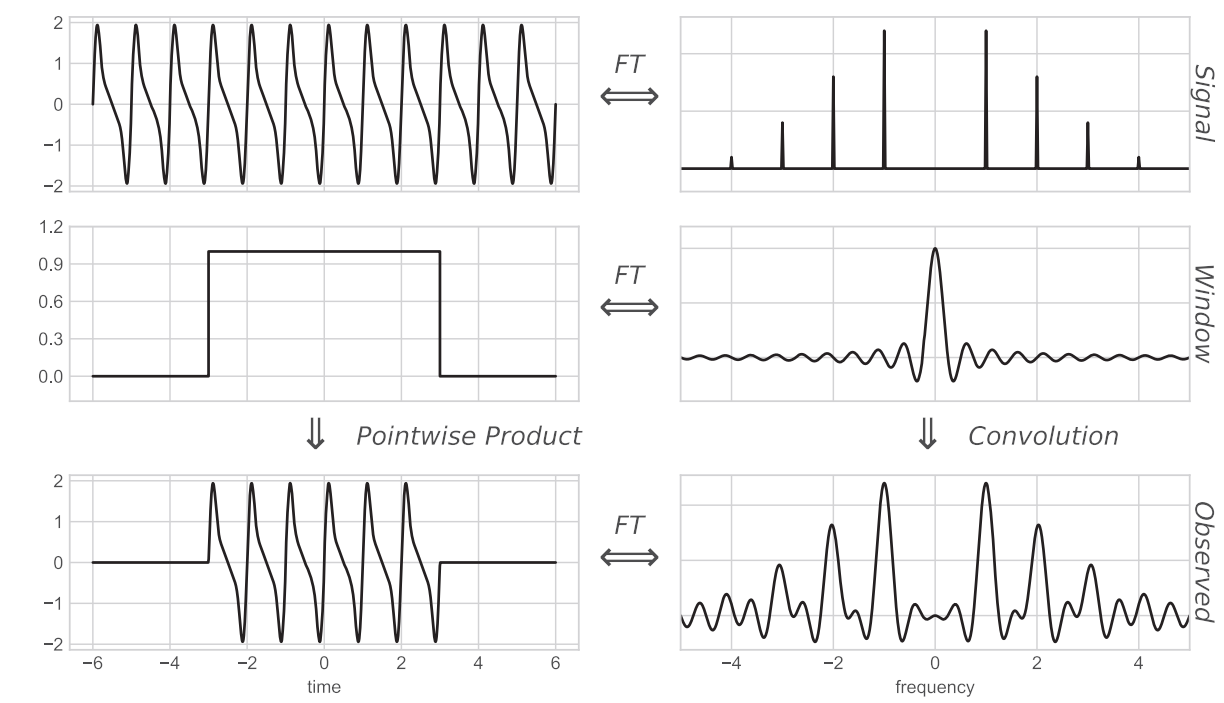
Bir sinyali (sol üst), sonlu bir zaman çerçevesinde (gözlem çerçevesi, sol orta) sürekli gözlemekle onun o gözlem penceresi çerçevesinde sınırlı haliini elde ederiz (sol alt). Bu sınırlı sinyal, değişimle gözlem çerçevesinin çarpımına, Fourier dönüşümü ise konvolüsyon teoremi gereğince onların konvolüsyonuna eşittir.
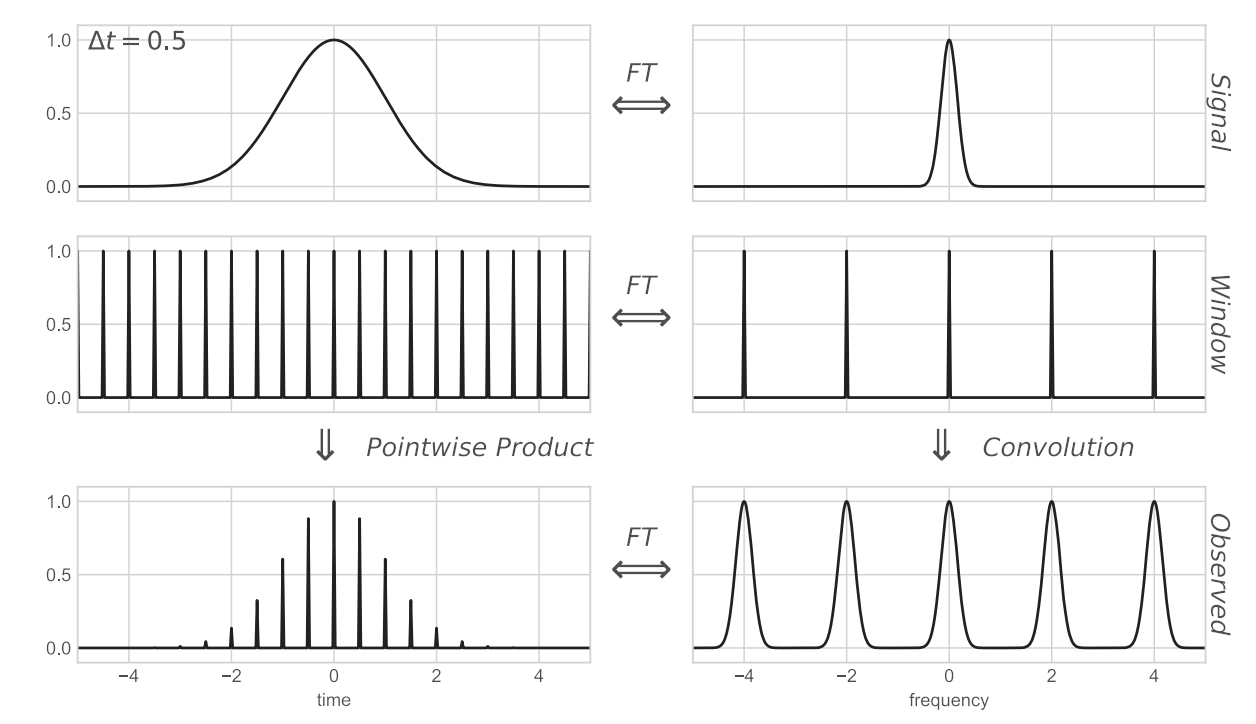
Sonlu aralıklarla, anlık olarak yapılan gözlemler ise Delta fonksiyonu yapısındaki bir gözlem penceresiyle ifade edilir (sol orta). Bu durumda sinyal sol alttaki şekilde gözlenir ve Fourier dönüşümü ise sağ alttaki gibidir.
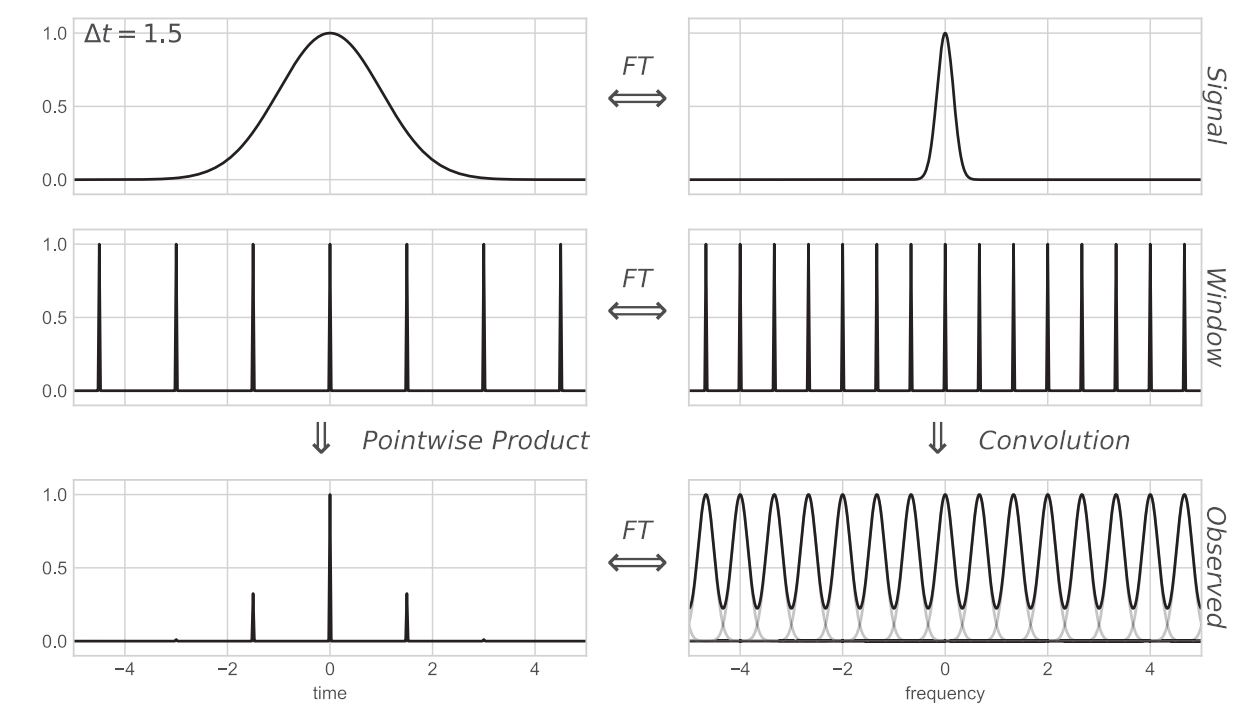
Sinyalin daha yavaş örneklenmesi durumunda Fourier dönüşümündeki pikler birbirinden ayırlamazlar (aliasing). Bu durum daha önce karşılaştığımız Nyquist frekansının altında gözlem yapıldığı anlamına gelir. Görsel olarak sağ üstteki gözlemin Fourier dönüşümü, sağ ortadaki gözlem penceresinin Fourier dönüşümü “tarağının” (sağ orta) iki dişi arasna sığmamaktadır.
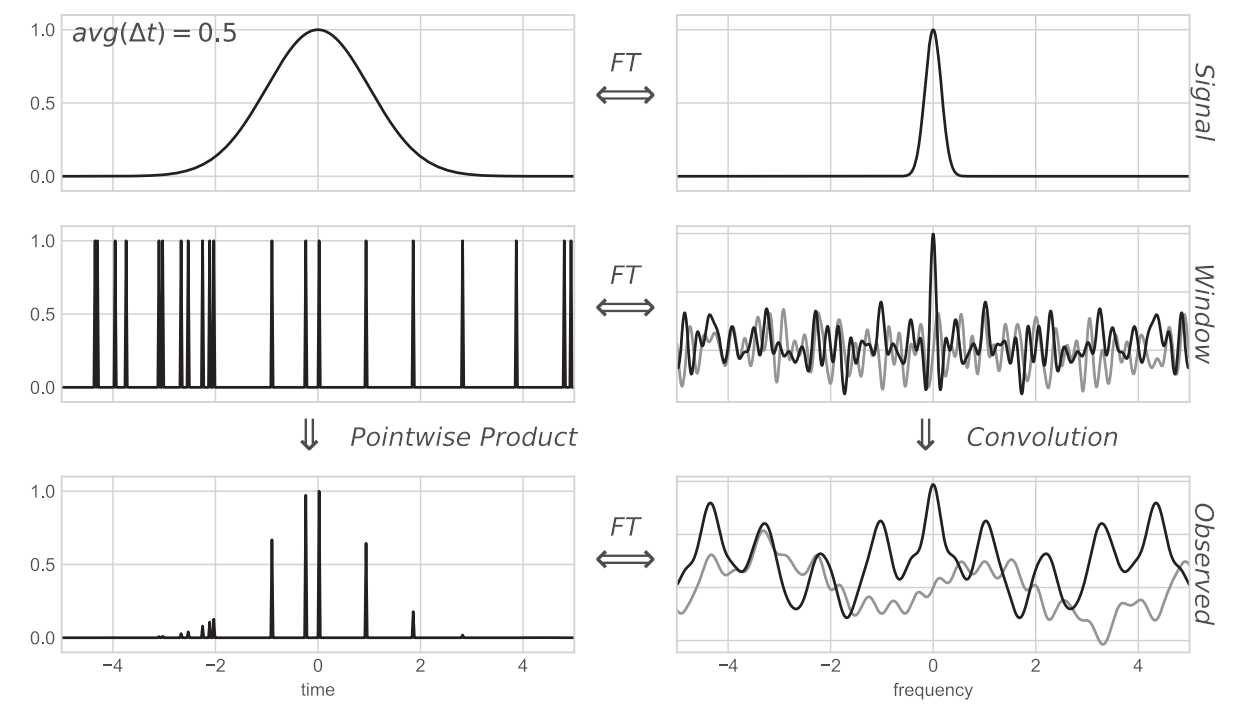
Sinyalin düzensiz örneklenmesi durumunda Fourier dönüşümündeki pikleri birbirinden ve gürültüden ayırmak giderek güçleşir. Ancak düzensiz örnekleme durumunda Nyquist frekansının gözlenebilecek en yüksek frekans limitini belirlemekte artık kullanılamaz.
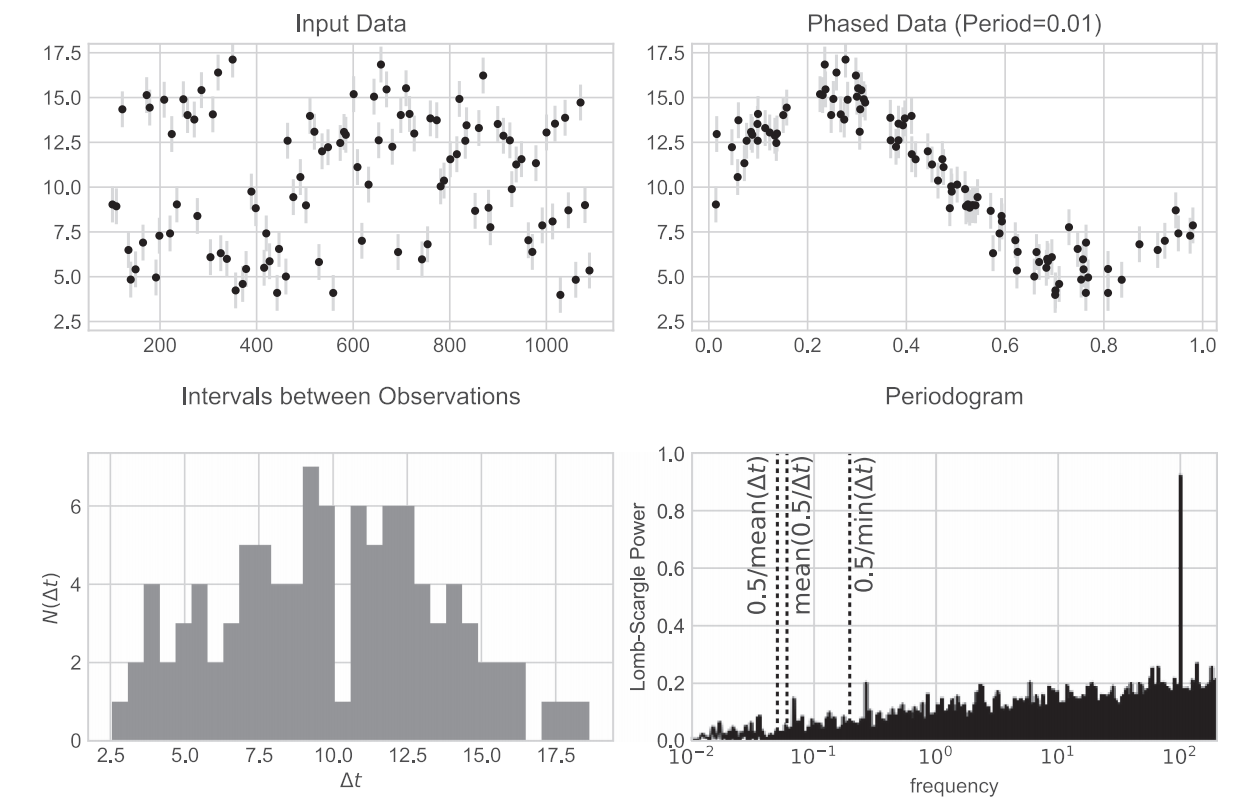
Nyquist frekansının düzensiz alınan veri için bir üst frekans limiti olarak kullanılamayabileceğine bir veri örneği. Üst paneller, 100 frekanslı (yani 0,01 birim dönemli) gürültülü bir sinüsoidal olan verileri, sol alttaki panel, gözlem noktası aralıkların histogramını göstermektedir; minimum aralık 2.55 birimdir, yani sinyalin en yakın gözlem çifti arasında 250'den fazla tam çevrim bulunmaktadır. Bununla birlikte, periodogram (sağ altta), ortalama veya minimum örnekleme oranına dayalı Nyquist frekansının öngördüğünden daha büyük frekanstaki değişim belirlenebildiğini açıkça göstermektedir.
Lomb Scargle Periyodogramı¶
Düüzensiz aralıklarla veri alınması durumunda klasik periyodogramla yapılan analizlerde ne gibi problemlerin yaşanabileceğini görmüş olduk. Eyer & Bartholdi (1999) tarafından önerildiği şekilde yapılandırılmış “yarı-düzenli” gözlem çerçevelerinde dahi bu etkilerden kaçınılamayabilir (daha geniş bir açıklama için bkz. VanderPlas 2018 ve Demming 1975).
Klasik periyodogram Scargle (1982)’de önerildiği şekilde düzensiz aralıklarla alınan veri üzerinde frekans analizi yapmak üzere modifiye edilebilir. $A$, $B$ ve $\tau$ frekansa bağlı keyfi fonksiyonlar olmak üzere bu modifikasyon;
$$ P_N (\nu) = \frac{1}{N} \{ (\sum_{i=1}^{N} x(t_i) e^{-2 i \pi \nu t_i})^2 = \frac{1}{N} \{ (\sum_{i=1}^{N} x(t_i) sin(2 \pi \nu t_i))^2 + (\sum_{i=1}^{N} x(t_i) cos(2 \pi \nu t_i))^2 \} $$$$ P_N (\nu) = \frac{A^2}{2} \{ (\sum_{i=1}^{N} x(t_i) cos(\pi \nu (t_i - \tau)))^2 + (\sum_{i=1}^{N} x(t_i) sin(2 \pi \nu (t_i - \tau))^2\} $$olarak elde edilebilir. $A$, $B$ ve $\tau$ frekansa bağlı keyfi fonksiyonları öyle seçilebilir ki:
1) periyodogram eş zaman aralıklarında alınmış veri için klasik periyodograma indirgenebilir,
2) periyodogramın dağılımı analitik olarak hesaplanabilir,
3) periyodogram verideki eş zaman kaymalarından (evre farkı) etkilenmez.
Bu şekilde seçilen $\tau$,
$$ \tau = \frac{1}{4 \pi \nu} tan^{-1}(\frac{\Sigma_n sin(4 \pi \nu t_i)} {\Sigma_n cos(4 \pi \nu t_i)} $$olmak üzere bu özellikleri sağlayan Lomb-Scargle Periyodogramı aşağıdaki şekilde elde edilmiş olur:
$$ P_{LS} (\nu) = \frac{1}{2} \frac{ (\sum_{n} x(t_i) cos(\pi \nu (t_i - \tau))^2}{\sum_{n} cos^2(\pi \nu (t_i - \tau))} + \frac{(\sum_{n} x(t_i) sin(2 \pi \nu (t_i - \tau))^2} {\sum_{n} sin^2(\pi \nu (t_i - \tau))} $$Bu "modifiye" periyodogram klasik periyodogramdan payda olarak ifadeye $N/2$ yerine giren $\sigma_n sin^2(2 \pi \nu t_i)$ ve $\sigma_n cos^2(2 \pi \nu t_i)$ ile ayrılmaktadır ki; tüm evre aralığının bütünüyle kapsanacağı eş aralıklı veri için $N / 2$ bu fonksiyonların beklenen değeridir. Bu nedenle pek çok durumda Lomb-Scargle periyodogramı ile klasik (Schuster) periyodogramı arasındaki fark çok küçüktür.
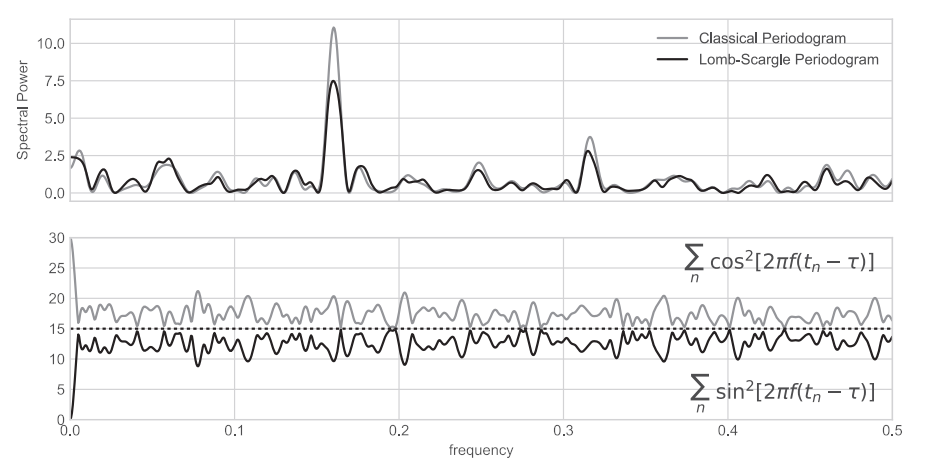
Bir sinüsoid fonksiyonla elde edildikten sonra üzerine Gaussyen gürültü elde edilmiş 30 noktanın klasik ve Lomb-Scargle periyodogramı (üstte) ve Lomb-Scargle periyodogramının oluşturulması için kullanılan payda terimlerinin frekansla değişimi (altta).
Bu ifade ve yöntem aslında eldeki veriye her frekans ($\nu$) için en küçük kareler yöntemiyle sinüs fonksiyonları uyumlamakla (fit etmekle) özdeştir. Periyodogram her frekansta veriyle ona uyumlanan (aşağıdaki yapıda) sinüsoidallerden artıklara ($\chi^2$ değerlerine) ölçeklidir (Lomb 1976).
$$ y(t; \nu) = A_{\nu} sin(2 \pi \nu (t - \phi_\nu) $$Her frekansta veriye uyumlanan sinüsoida fonksiyonun genliği ($A_\nu$) ve evresi ( $\phi_\nu$) farklıdır. Her frekans için veri ile arasındaki fark kareler toplamı ($\chi^2$) en küçük olacak sinüsoidal model aranır.
$$\chi^2(\nu) = \sum_{n} (y_n - y(t_n, \nu))^2 $$Scargle (1982) modfiye ettiği periyodogram ifadesi ile her bir $\nu$ frekansı için en küçük kareler minimizasyonu yöntemiyle elde edilen modelin $\chi_\nu^2$ 'nin frekansla değişiminin özdeş olduğunu göstermiştir.
$$ P(\nu) = \frac{1}{2} (\chi_0^2 - \chi(\nu)^2) $$Burada $\chi_0^2$ , herhangi bir frekanstaki değişmez bir referans modeldir. $\chi^2$ Gaussyen gürültünün ($\sigma_n$) ve korele gürültünün ($\Sigma$ kovaryans matrisi göstermek üzere) varlığında aşağıdaki şekide ifade edilebilir.
$$ \chi^2(\nu) \equiv \sum_{n} (\frac{y_n - y_{model}(t_n; \nu)}{\sigma_n})^2 $$$$ \chi^2(\nu) = (y - y_{model})^T \Sigma^{-1} (y - y_{model}) $$Periyodograma getirilmesi gereken bir diğer modifikasyon sinyalin merkezi ile ilgilidir. Periyodogram, bu modifikasyon yapılmadığı sürece sinyalin ortalama değer etrafında bir salınım olduğunu varsayar. Eldeki veri bir sebeple (cisim sönükleştiği zaman gözlenememesi gibi) ortalamanın olması gerektiği yerden farklı bir orta değer ($y_0$) etrafında salınıyorsa, her frekansta uyumlanacak sinüsoidallere bu değerin eklenmesi gerekir.
$$ y_{model} = y_0(\nu) + A_{\nu} sin(2 \pi \nu (t - \phi_\nu) $$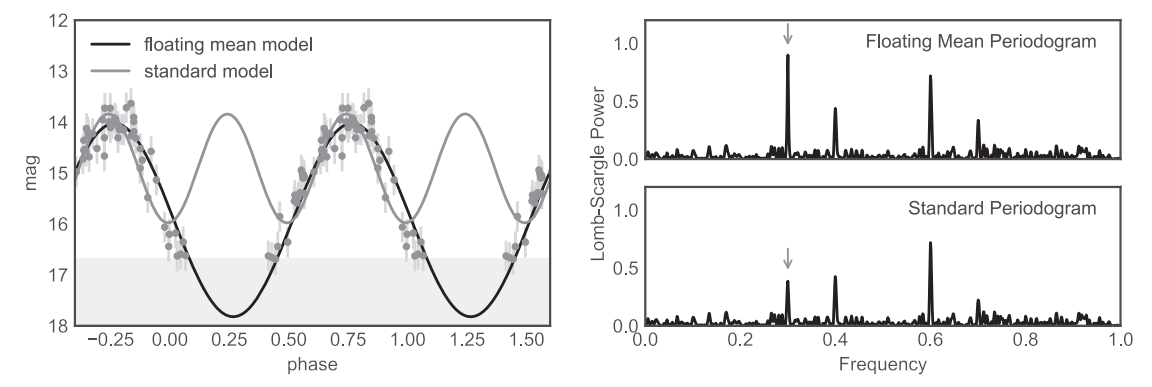
Ortalama değeri değiştirerek yapılan modifikasyonun bu düzeltme yapılmadan elde edilen periyodogramda baskılanan (0.3 frekans civarında) frekansın ortaya çıkarılmasını sağladığ görülmektedir. Değişimin gerçek ortalama parlaklık etrafından olmamasını nedeni bu örnekte cisim sönükleştiğinde gözlenememesidir.
Standart Lomb-Scargle periyodogramlarına getirilebilecek bir diğer modifikasyon veriyi tek bir sinüsle değil de birden fazla frekans (çoklu frekans) içeren modellerle uyumlamaya çalışmak olabilir. Bu aşağıdaki gibi ana frekansın $k$ katında frekansa sahip modelleri de birlikte uyumlamakla sağlanabilir.
$$ y_{model}(t;\nu) = A_(\nu)^0 + \sum_{i=1}{K} A_{\nu}^{(k)} sin(2 \pi \nu (t - \phi_\nu^{(k)}) $$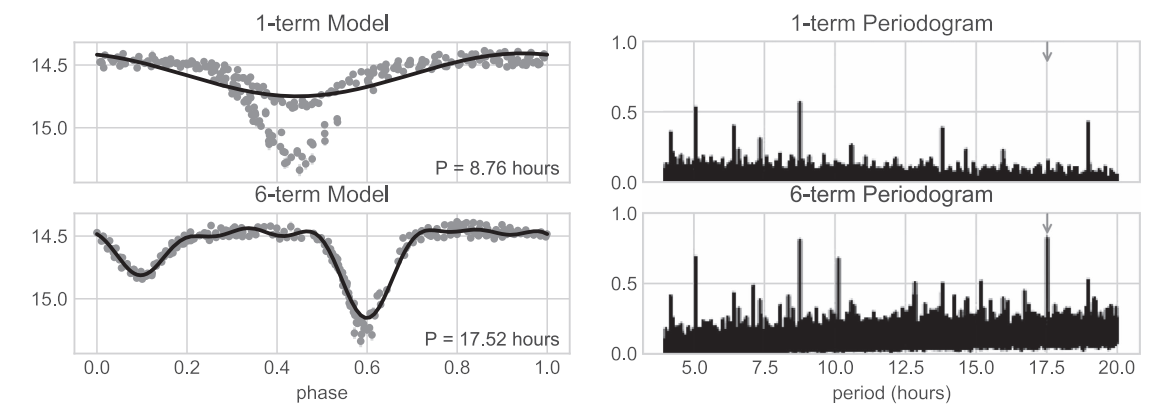
Klasik periyodogramda olduğu gibi $N$ (nokta sayısı) yeterince büyük olduğunda $\nu_1$ frekansındaki güç değeri yine $A^2 N / 4$ ‘e yakınsar. Lomb-Scargle periyodogramına dayalı genlik spektrumunda genlik
$$ A_{LS} = \sqrt{\frac{4 P_{LS}(\nu)}{N}} $$ile verilir. Sonuç olarak, Lomb-Scargle periyodogramının önemli bir avantajı eş aralıklı ve / veya sinüsoidal olmayan veriye de uygulanabilmesidir. Bu yöntem de temelinde en küçük kareler yöntemiyle sinüs uyumlamaları (fiti) ile aynı sonucu verdiği için parametrik olmayan yöntemlerin (en küçük kareler yöntemiyle iteratif sinüs fiti) etkinliğini göstermek bakımından önemlidir.
scipy.signal.lombscargle Lomb (1976) tarafından eşit aralıklarla alınmamış (eş frekansla örneklenmemiş) zayıf periyodik sinyallerin analizi için üretilen ve Scargle (1982) tarafından daha da geliştirilen Lomb-Scargle periyodogramlarının üretilmesine olanak sağlayan bir fonksiyondur. Normalizasyon yapılmazsa (normalize = False), yeterince büyük $N$ için $A$ genliğine sahip bir harmonik sinyal söz konusu olduğunda $(A^2) N / 4$ değerini alır. Normalizasyon ($normalize = True$), sabit referans modelden (0 noktasına) farklara göre yapılır. Yine öncelikle bir sentetik veri seti üretelim.
import numpy as np
from scipy import signal
import matplotlib.pyplot as plt
A = 2. # genlik
w = 1. # acisal frekans
phi = 0.5 * np.pi # aci
N1 = 1000
N2 = 100000
# Veriyi farkli zaman araliklarinda alinmis bir veriye
# donusturmek uzere karsilastirma amaciyla kullanacagimiz parametre
atla = 0.9
# ortalamasi 0, standart sapmasi 1 olan bir normal dagilimdan
# 1000 nokta secelim
r = np.random.rand(N1)
# 0.01 ile 10pi arasinda 1000 noktadan olusan bir x eksenimzi olsun
x = np.linspace(0.01, 10*np.pi, N1)
# dagilimdan secilen sayi 0.9'dan buyukse alalim
# onun karsilik geldigi indeksteki x'i alalim yoksa almayalim
x = x[r >= atla]
# Sinyalimizi hazırlayalim
y = A * np.sin(w*x+phi)
plt.plot(x,y,'r-')
# Biraz sentetik gurultu ekleyelim
y += np.random.normal(size=len(x))
plt.plot(x,y,'b+')
plt.xlabel("t (saniye)")
plt.ylabel("y")
plt.show()
Daha sonra da bu veriyi Lomb-Scargle periyodogramı ile analiz edelim.
# Lomb-Scargle periyodogramini hesaplayacagimiz frekanslar
f = np.linspace(0.01, 10, N2)
pgram = signal.lombscargle(x, y, f, normalize=False)
pik_frekans = f[pgram.argmax()]
pik_genlik = np.sqrt(pgram.max())/4
print("Pikin maksimumu {:.4f} Hz'te ve genligi {:.4f}".\
format(pik_frekans, pik_genlik))
plt.plot(f,pgram)
plt.xlabel("f (Hz)")
plt.ylabel("$P_{LS} [A^2 N / 4]$")
plt.axvline(x=pik_frekans,c="r",ls="--")
plt.show()
Görüldüğü gibi bulunan p-değeri (0.11), seçilen istatistiksel anlamlılık seviyesinden ($\alpha = 0.025$) büyük olduğu için $H_0$ hipotezi reddedilemez. Yani rastgele süreçlerle, şans eseri, bu sonucu elde etmenin olasılığı seçilen istatistiksel anlamlılık seviyesinden büyüktür.
Spektral Sızma¶
Konuyu anlamak üzere ncelikle sürekli ve 2 Hz frekansına sahip basit bir sinüsoidal fonksiyonu düşünelim. $x(t)=cos(4 \pi t$). Bu sinyalin sürekli Fourier dönüşümü $X(\nu) = δ(\nu ± 2) verir.
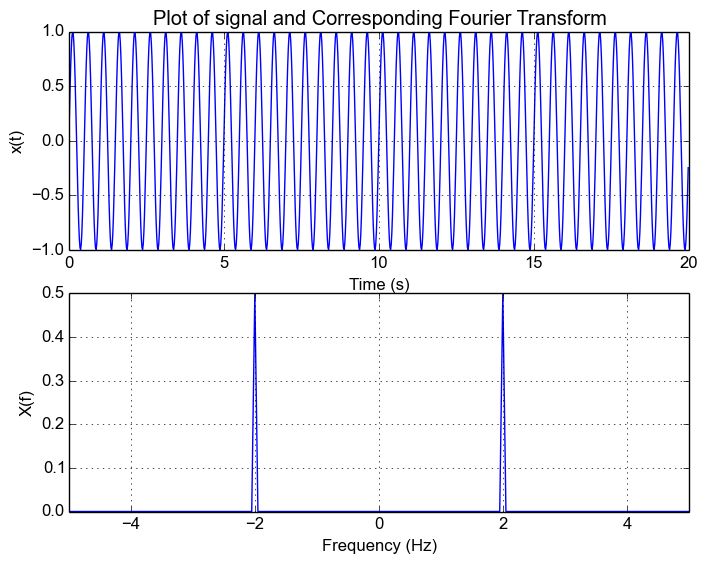
Ancak gerçekte biz bu $(-\infty, +\infty)$ aralığındaki sinyalin sadece bir bölümünü, bir gözlem penceresi (window function) dahilinde gözleriz. $x^(t) = x(t) w(t)$. Gözlem penceresiyle çerçevelenmiş bu sinyalin Fourier dönüşümü $X^(\nu)=X(\nu) ∗ W(\nu)$ şeklinde verilir (çarpımın Fourier dönüşümünün konvolüsyon olduğunu hatırlayınız). Burada $W(\nu)$ spektral pencere (ing. spectral window) adını alır.
Diyelim ki gözlem penceremiz bir dikdörtgen olsun (astronomide genellikle böyledir). Ölçümümüzü $\Delta t = t_2 - t_1$ aralıklarla alıyor olalım. Bu durumda gözlem penceremiz $w(t) = u(t−t_1) - u(t−t_2)$ ve frekans tanım kümesinde karşılık geldiği gözlem penceresi $W(\nu) = e^{-2i \pi \nu t_1} sinc(\Delta t_2) \Delta t$ olur. Bu noktada kutu fonksiyonunun Fourier dönüşümünün bir $sinc(x) = (sin (\pi x / \pi x)$ fonksiyonu olduğunu hatırlayınız.
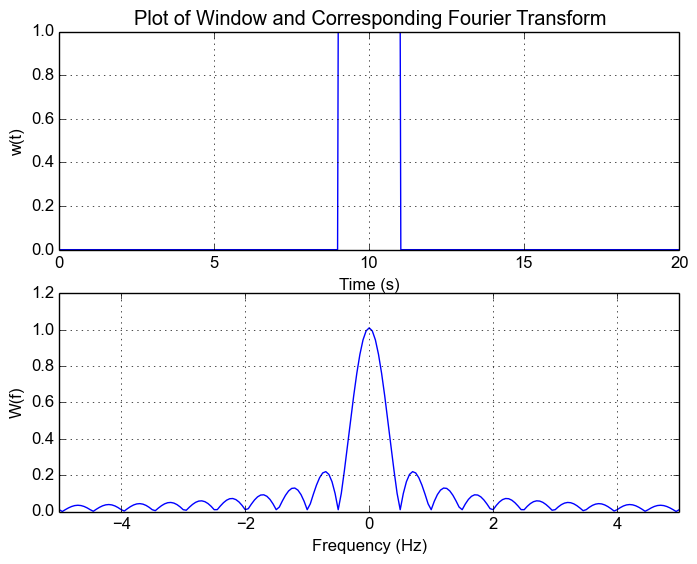
Bu durum diğer frekanslara sızan piklere (side-lobe) yol açar.
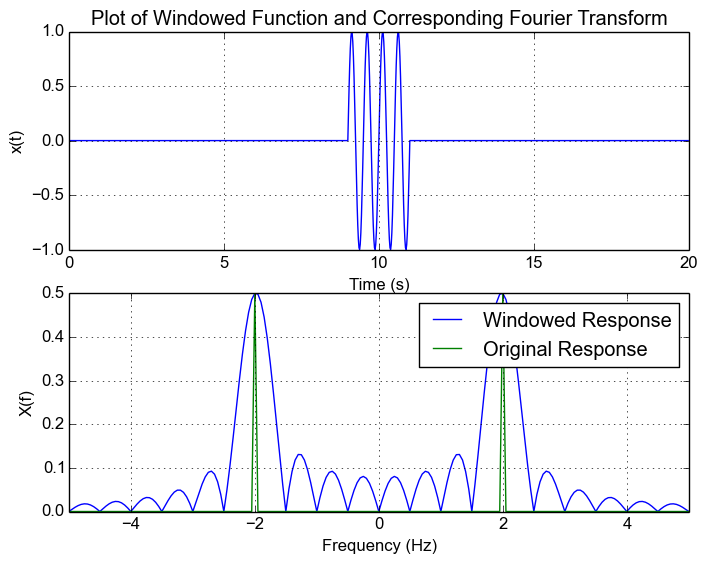
Spektral sızma, gözlenen çevrim sayısının tam olmamasından da kaynaklanır. Özünde bu da bir gözlem penceresi etkisidir.
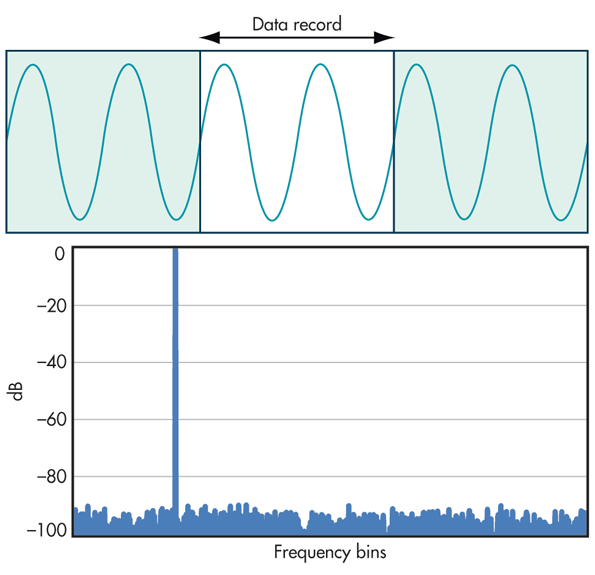
Tam sayıda (2) çevrimin gözlendiği durum. Üstte zaman serisi altta Fourier dönüşümü görülmektedir.
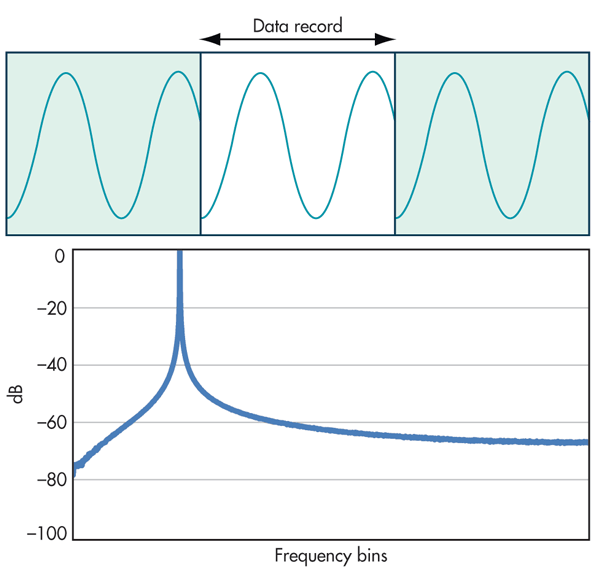
Bu durum verinin tamamıyla yanlış değerlendirilmesine ve olmayan değişimlere yönelinmesine dahi sebep olabilir.
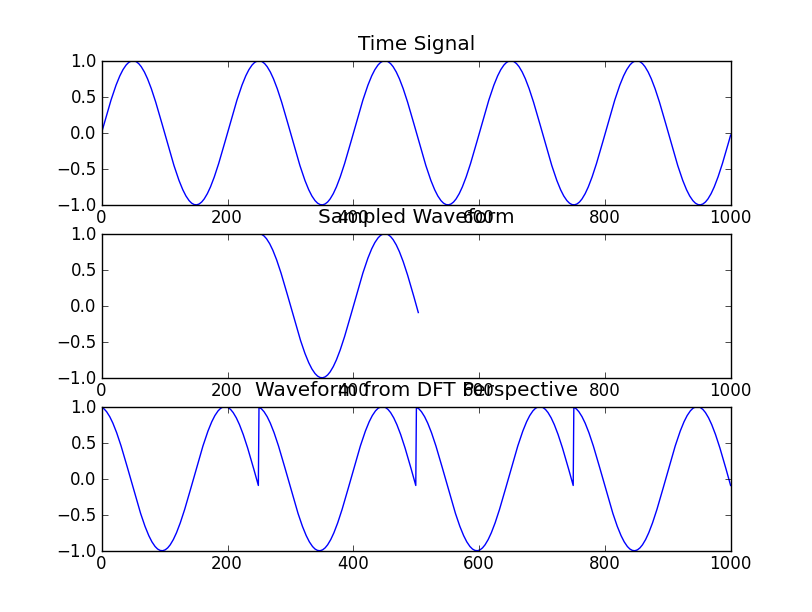
Üstte $(-\infty, +\infty)$ aralığında sürekli sinyal, ortada gözlem penceresi çerçevesinde gözlenen sürekli bantla sınırlı (ing. Band-limited) sinyal, en altta bu sinyale uygulanan Fourier dönüşümünün ters dönüşümünden elde edilen sinyal görülmektedir.
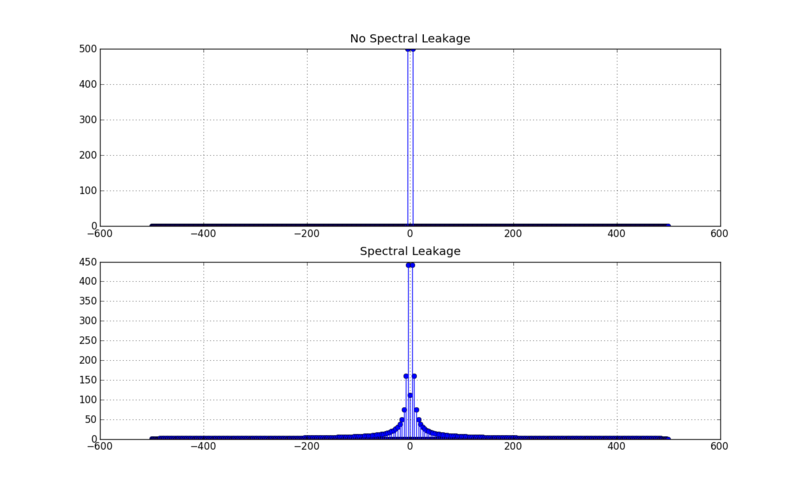
Örnek Frekans Analizi¶
Astronomide verinin içerisinde bulunan dönemliliğin belirlenmesi kritik önem taşır. Dikine hız ya da geçiş yöntemiyle keşfedilen ötegezegenlerin ya da çift yıldızların yörünge, zonklayan yıldızların zonklama dönemlerinin belirlenmesi gibi pek çok uygulama alanı bulunan bu konuyla ilgili bir örnek yapalım. Astronomide çoğu zaman sadece geceleri gözlem yapılabilmesi, bazı cisimlerin yılın sadece belirli dönemlerinde gözlenebilmesi ve hava koşullarının her zaman uygun olmaması gibi nedenlerle çoğunlukla düzensiz, sık aralıklı olmayan veri alınır. Bu nedenle de bu tür veride frekans analizi için daha uygun olan Lomb-Scargle periyodogramları kulllanılmaktadır.
Python'da scipy.signal.lombscargle ve astropy.timeseries.LombScargle Lomb-Scargle periyodogramları oluşturmak ve bu periyodogramları kullanarak frekans analizi yapmak için sıklıkla kullanılmaktadır. Bunlardan astropy.timeseries.LombScargle doktora çalışmasını astrofizik alanında yapan Jake Van der Plas tarafınan yazıldığı ve astronomide ihtiyaç duyulan temel parametreleri hızlı sağladığı gerekçesiyle astronomlar tarafından daha sık kullanılmaktadır.
Aşağıda bir ötegezegenin TESS uzay teleskobu tarafından 120 saniyelik poz süresiyle alınmış ve bazı istenmeyen etkilerden arındırılmış ışık eğrisi görülmektedir.
from astropy.io import ascii
lc = ascii.read("veri/otegezegen_TESS_verisi.txt")
lc.columns
Verinin başlığına bakıldığında zamanın BJD_TDB, normalize akının normflux, hatasının fluxerr sütunlarında bulunduğu görülmektedir.
from matplotlib import pyplot as plt
zaman = lc['BJD_TDB']
aki = lc['normflux']
hata = lc["fluxerr"]
plt.errorbar(zaman,aki,yerr=hata)
plt.show()
Ötegezegenin yıldızının önünden geçtiği sıradaki akı kayıpları ışık eğrisi üzerinden tespit edilebilmektedir. Birine yakından bakalım.
zoom_mask = (zaman > 2458818.5) & (zaman < 2458819.5)
plt.errorbar(zaman[zoom_mask],aki[zoom_mask],yerr=hata[zoom_mask])
plt.show()
Bu örnekte amacımız ötegezegenin yıldızı önünden kaç günde bir geçtiğini, yani yörünge dönemini bulmak için Lomb-Scargle periyodogramlarına dayalı bir frekans analizi yapmaktır. Bunun için öncelikle bu ışık eğrisinin astropy.timeseries.LombScargle fonksiyonuyla periyodogram nesnesini oluşturmalıyız. Fonksiyonun tüm parametreleri ve detaylı bilgi için bkz.
from astropy.timeseries import LombScargle
ls = LombScargle(zaman, aki)
Bu nesne bir frekans analizi için ihtiyaç duyulan bütün nicelikleri barındırmaktadır. Öncelikle periyodogramı autopower() fonkisyonuyla oluşturup, çizdirerek işe başlayalım. Zaman verimizi gün biriminde olduğu için, frekans ekseninin birimi 1 / gün olmalıdır. Güç ekseninin birimi ise güç yoğunluğunu göstermektedir ve istenirse normalize edilebilir.
frekans,guc = ls.autopower()
plt.xlabel("Frekans (1 / gun)")
plt.ylabel("Guc")
plt.plot(frekans,guc)
plt.show()
Görüldüğü gibi üç baskın frekans öne çıkmaktadır. Bu frekanslardan ~750 1 / gün'lük frekans TESS'in kısa poz süreli (ing. short cadence) veri aldığı modunun frekansıdır ki gözlem penceresi fonksiyonunun nasıl güç spektrumunda göründüğünü çok güzel örneklemektedir. TESS kısa poz süres modunda 120 saniyede bir veri aldığı için
sc = 120
sc_frek = 1 / 120 * 86400
print("TESS kisa poz suresi modunun frekansi {:.4f} 1/gun'dur".format(sc_frek))
Ayrıca bu frekansın 1. harmoniği olan frekans da 1400 1 / gun civarında açıkça görülebilmektedir.
Biz ilgilendiğimiz gezegenin yörünge dönemi için daha düşük frekanslara bakmalıyız. Bu nedenle periyodogramımızı kısıtlamalıyız. Yörünge döneminin 0.5 günden daha kısa olamayacağını düşünerek, ilgilendiğimiz maksimum frekansı 1 / 0.5 gün = 2.0 1/gün olarak belirleyelim. Bunu autopower fonksiyonunun maximum_frequency parametresini 2.0'a ayarlayarak yapacağız. İstenirse bir minimum limit de minimum_frequency ile belirlenebilir.
frekans,guc = ls.autopower(maximum_frequency=2.0)
plt.xlabel("Frekans (1 / gun)")
plt.ylabel("Guc")
plt.plot(frekans,guc)
plt.show()
Ana frekans en düşük frekansta, onun tam katları olan harmonikleri ise yanında ondan daha küçük pikler olarak kendini açıkça göstermektedir. Ayrıca spektral sızma kaynaklı yan pikleri (ing. side lobes) rahatlıkla görebiliyoruz. Şimdi verinin içindeki maksimum genlikli pikin frekansını bulmak üzere, spektral gücü gösteren $guc$ dizisinin maksimum değerinin karşılık geldiği frekansı bu değerin karşılık geldiği indeksi $frekans$ dizisinde yerine koyarak bulalım.
import numpy as np
maks_frekans = frekans[np.argmax(guc)]
print("Maksimum gucteki frekans {:.4f} 1/gun degerindedir".format(maks_frekans))
Ancak frekanstan daha çok biz bu frekansın karşılık geldiği yörünge dönemini bilmek isteriz. Ancak frekans ($f$) ile dönem ($P$) arasındaki ilişki oldukça basittir: $P = \frac{1}{f}$
donem = 1 / maks_frekans
print("Maksimum frekansin karsilik geldigi yorunge donemi {:.4f} gundur.".format(donem))
Hassas gözlenmiş sadece 6 geçişten gezegenin yörünge dönemini belirleyebildik. Şimdi bu yörüngenin çembersel olduğunu, dolayısıyla değişimin sinusoidal olduğu (ki geçiş sinyali sinüsoidal bir sinyal değildir ama biz tüm periyodik sinyallerin sinüsoidal fonksiyonlara Fourier dönüşümleri ile dönüştürülebildiğini biliyoruz) varsayımıyla genliğini bulmaya çalışalım. y-ekseninin Spektral Güç Yoğunluğu ile (ing. Power Spectral Density, PSD) ifade edilmesi durumunda genliğin $P_{LS} = \sqrt{frac{4 A_{\nu}}{N}}$ bağıntısından bulunabileceğini biliyoruz. Ancak astropy.LombScargle periyodogramında y-eksenindeki güç doğrudan genliğin karesidir. Dolayısı ile maksimum güçteki genliği bulmak için öncelikle maksimum gücü ve sonra da onun karekökünü bulmamız yeterli olacaktır. Amacımıza basit numpy fonksiyonları ve güç ekseninin PSD biriminde olduğunu garanti etmek üzere normalizasyon parametresini "psd" değerine ayarlayarak ulaşabiliriz.
maks_guc = np.max(guc)
maks_genlik = np.sqrt(ls.power(maks_frekans, normalization='psd'))
print("Maksimum frekanstaki genlik: {:.4f} ".format(maks_genlik))
Söz konusu ötegezegenin neden olduğu ışık kaybının %2.78 düzeyinde olduğunu görüyoruz. Dikine hız gibi veriler için genlik yerine yarı genliğin ($K$) kullanıldığını, bu nedenle bulunan genliğin 2'ye bölünmesi gerektiini hatırlatalım.
Yanlış Alarm Olasılığı¶
Genellikle astronomide bir parametre verirken onun hatasını da vermek isteriz. Ancak frekans analizinde ne maksimum gücün bulunduğu profilin genişliği, ne de yüksekliği bu değeri doğrudan vermez. Zira aslında pek çok frekans denenmekte ve bu frekanslardan veride bulunmayanları atılarak işlem yapılmaktadır. Bu nedenle pikin yükseklği Sinyal / Gürültü hakkında fikir verse de doğrudan bulunan frekansın (ya da ondan elde edilen dönemin) üzerindeki belirsizliğe eşit de değildir.
Bunun yerine değişimde bu frekansın bulunması durumunda analiz edilen verinin şans eseri elde edilme olasılığının 1'den farkını veren ve daha önceki derslerde işlediğimiz hipotez testi konusunda işlediğimiz Pearson p-değerine karşılık gelen Yanlış Alarm Olasılığı" (ing. False Alarm Probability, FAP) değeri kullanılır. Bu değer Lomb-Scargle periyodogram nesnesinin false_alarm_proability metoduna maksimum güç değeri (ya da hangi frekanstaki gücün yanlış alarm olasılığı bilinmek isteniyorsa o güç değeri) argüman olarak geçirilmek suretiyle kolaylıkla elde edilir.
fap_maks_guc = ls.false_alarm_probability(maks_guc)
print("Maksimum gucun yanlis alarm olasiligi FAP = {:g}".format(fap_maks_guc))
Görüldüğü üzere yörünge dönemine karşılık gelen frekansın değişimin frekansı olduğuna ilişkin $H_0$ hipotezinin doğru olması durumunda bu gözlemsel verinin şans eseri elde edilme olasılığı çok yüksek, başka bir deyişle örneklem hatası nedeniyle bu dönemliliğin bulunması olasılığı ise çok düşüktür.
Evrelendirme¶
Bir veri üzerindeki dönemlilik bulunduktan sonra genellikle veri analizcisi doğru bir dönem bulup bulmadığını denetlemek üzere verisini (ışık eğrisi, dikine hız ya da konum gibi) yörünge dönemine evrelendirerek grafiğe aktarmak ister. Örneğimizdeki ötegezegen geçişi için bu amaca astronomide çok iyi bilinen aşağıdaki yöntemle ulaşabiliriz.
Gözlenen olayın bir referans zamanı ($T_0$) ile bulunan dönem ($P$) için tüm gözlem zamanları (T)
$$ E = \frac{T - T_0}{P} $$formülüyle evreye dönüştürülebilir. Burada E, E.eeeee şeklinde ifade edilen çevrim değeridir (epoch) ve referans zamandan sonra (örneğimizde geçmişte gözlenmiş bir geçiş zamanı olabilir ya da ilk geçişin ortasındaki zaman kullanılabilir) geçen çevrim sayısını (E) ve kesrini (.eeeee) göstermektedir. Bu kesir istenen yörünge evresidir ve aşağıdaki python koduyla kolaylıkla hesaplanabilir.
T0 = 2454864.76684 # Gezegenin literaturdeki bir gecis zamani
# Epoch hesabi
E = (zaman - T0) / donem
# evre kesri
evre = E - E.astype(int)
# evreye gore kucukten buyuge siralama
indsirali = evre.argsort()
evre_sirali = evre[indsirali]
aki_sirali = aki[indsirali]
hata_sirali = hata[indsirali]
plt.errorbar(evre_sirali,aki_sirali,yerr=hata_sirali,c="b",fmt=".")
plt.xlabel("Evre")
plt.ylabel("Normalize Aki")
plt.show()
6 günlük verinin frekans analizinden bulunan dönem çok hassas olmadığından, kullanılan geçiş zamanı doğru olmayabileceğinden ya da gezegenin yörünge dönemi fiziksel bir nedenle zamanla değişiyor olabileceğinden evrelendirme yeterince iyi sonuç vermemiş olabilir. Bu nedenle aynı geçiş olayı defalarca gözlenir ve dönem giderek hassas hale getirilmeye çalışılır. Aynı evrelendirmeyi daha hassas bir dönemle yapmaya çalışalım.
P = 3.1915289
T0 = 2454864.76684 # Gezegenin literaturdeki bir gecis zamani
# Epoch hesabi
E = (zaman - T0) / P
# evre kesri
evre = E - E.astype(int)
# evreye gore kucukten buyuge siralama
indsirali = evre.argsort()
evre_sirali = evre[indsirali]
aki_sirali = aki[indsirali]
hata_sirali = hata[indsirali]
plt.errorbar(evre_sirali,aki_sirali,yerr=hata_sirali,c="b",fmt=".")
plt.xlabel("Evre")
plt.ylabel("Normalize Aki")
plt.show()
Bu kez hassas bir evre hesabı yapılmış görünüyor. 0 evreyi ortalamak üzere aşağıdaki python kodunu kullanabiliriz.
plt.errorbar(evre_sirali,aki_sirali,yerr=hata_sirali,c="b",fmt=".")
plt.errorbar(evre_sirali-1,aki_sirali,yerr=hata_sirali,c="b",fmt=".")
plt.xlim((-0.10,0.10))
plt.xlabel("Evre")
plt.ylabel("Normalize Aki")
plt.show()
Kaynaklar¶
Julius Orion Smith III Homepage, “Mathematics of the Discrete Fourier Transform” (DFT) www.fouriertransform.com
VanderPlas, 2018, “Understanding the Lomb–Scargle Periodogram”, ApJ&SS, 236, 16