Doç. Dr. Özgür Baştürk
Ankara Üniversitesi, Astronomi ve Uzay Bilimleri Bölümü
obasturk at ankara.edu.tr
http://ozgur.astrotux.org
Bu derste neler öğreneceksiniz?¶
Model Karşılaştırması ve En İyi Modelin Seçimi¶
- Merkezi Limit Teoremi
- Hipotez Testi
- t Dağılımı
- Serbestlik Derecesi
- Model ve Artıkları
- Bir Modelin Başarımına İlişkin Parametreler
- $\chi^2$ Dağılımı ve $\chi^2$ Testi
- Durbin Watson İstatistiği İle Model Başarımı Testi
- F Dağılımı ve F Testi
- Varyans Analizi ANOVA
- Akaike Bilgi Kriteri
- Bayesian Bilgi Kriteri
- Kaynaklar
Merkezi Limit Teoremi¶
Olasılık teorisinde, Merkezi Limit Teoremi (ing. Central Limit Theorem, CLT), herhangi bir rastgele değişenin kendisi normal dağılıyor olmasa dahi, o rastgele değişenin olası tüm değerlerinden oluşturulan çok sayıdıa örnekleminin ortalamalarının (bu örneklemlerin kendisi de normal dağılmak zorunda değildir) normal dağılacağını söyler. Teorem olasılık teorisinde büyük önem taşır. Çünkü teoremden normal dağılımlar için geçerli olasılıksal ve istatistiksel yöntemlerin diğer dağılım türlerini de içeren birçok probleme uygulanabileceği sonucu çıkarılabilir. Diyelim ki seçilmiş 1000 Sefeid türü değişenin zonklama dönemleri normal dağılmıyor olabilir. Ancak çok sayıda (örneğin 100'er tane) Sefeid içeren çok sayıda örneklemin (örneğin 100 küresel kümenin) ortalama zonklama dönemlerinin dağılımına bakıldığında normal dağılım gösterdikleri görülür. Normal dağılım ve örnek için bkz.
Bir örnekle merkezi limit teoremini görselleştirerek anlamaya çalışalım. Pek çok sınıfa aynı anda uygulanan bir sınav düşünelim. Sınavda alınan notların sınıflar içinde ve sınıflarının ortalamasının da genelde nasıl dağıldığına bakalım. Öncelikle 50 öğrenciden oluşan bir sınıf için numpy.randint() fonksiyonuyla rastgele belirlenmiş sınav notlarından oluşan bir örneklem oluşturalım.
import numpy as np
# rastgele sinav notunu ayni degerleri verecek sekilde
# ayarlayalim (seed edelim)
np.random.seed(1)
# notlarin tamsayi oldugunu varsayarak 50 rastgele
# notu 40 ile 70 arasinda olusturalim.
notlar = np.random.randint(40, 70, 50)
print(notlar)
print('Sinif ortalamasi: {:.2f}'.format(notlar.mean()))
print('Standart sapmasi: {:.2f}'.format(notlar.std()))
Sınıf içindeki not dağılımını yukarıda gördük; bir de histogramına bakalım.
from matplotlib import pyplot as plt
# sinif ici not dagilimi
plt.hist(notlar)
plt.show()
Hiç de normal dağılıyormuş gibi görünmüyor. Nitekim numpy.random.randint() sınırları verilen (örneğimizde 40 ve 70) bir tekdüze dağılımdan istenen büyüklükte (örneğimizde 50) bir rastgele örneklem oluşturur. Şimdi örneklem sayısını 1 sınıftan 1000 sınıfa çıkaralım ve sınıfların ortalamasının nasıl dağıldığna bakalım.
import matplotlib.pyplot as plt
# yine ayni sekilde istikrarli bir orneklem icin
# rastgele tam sayi ureticisini seed edelim.
np.random.seed(1)
# Yine 40 ile 70 arasindaki notlar icin
# bu kez 1000 siniftan olusan orneklemimizdeki
# her bir sinifin ortalamasini alip sinif_ortalamalari
# degiskenine alalim
sinif_ortalamalari = [np.mean(np.random.randint(40, 70, 50)) for i in range(1000)]
# dagilimi bir histogramla gosterelim.
plt.hist(sinif_ortalamalari)
plt.show()
print('Sinif ortalamlarinin ortalamasi {:.2f}'.format(np.mean(sinif_ortalamalari)))
print('Sinif ortalamlarinin standart sapmasi {:.2f}'.format(np.std(sinif_ortalamalari)))
Her ne kadar tek bir sınıf içindeki not dağılımı normal değil tekdüze (uniform) olsa da 1000 sınıfın ortalamaları normal dağılmaktadır. Bir sınıf içinde 8.65 olan standart sapma değerinin de 1000 örenklemin ortalamaları söz konusu olduğunda 1.21'e kadar düştüğünü görüyoruz.
Örneklem Dağılımı (ing. Sampling Distribution): Bu şekilde normal dağılmıyor olsa dahi örneklemlerin ortalamalarının dağılımı örneklem dağılımı adını alır.
Ortalamanın Beklenen Değeri (ing. Expected Value of the Mean): Örneklem dağılımının ortalama değeri popülasyonun ortalaması için beklenen değerdir. Bir başka deyişle, bir popülasyondan rastgele seçilen örneklemlerin ortalamalarının dağılımının ortalaması o popülasyonun ortalamasının beklenen değeridir.
Standart Hata (ing. Standard Error): Örneklem dağılımının ortalama değerinin standart sapmasıdır. Dolayısı ile popülasyon ortalamasının standart sapmasının da beklenen değeridir. Tıpkı standart sapmanın herhangi bir ölçümün ortalamadan sapmasının bir ölçütü (tüm sapmaların ortalaması) olduğu gibi, standart hata da bireysel örneklemlerin ortalamalarının, örnek dağılımının ortalamasından sapmasının ölçütüdür. Bu nedenle de standart hatadır çünkü ortalamaların dağıımının (örneklem dağılımının) ortalamasının popülasyonun ortalamasını ne kadar temsil ettiğine olan güvenimizin bir ölçütüdür.
Örneklemlerin ortalamasının bir dağılımı olduğu gibi diğer istatistiklerin de (standart sapma, korelasyon katsayısı, $\chi^2$, ...) birer dağılımı vardır. Aynı şekilde ortalamaların ortalamasının bir standart hatası olduğu gibi diğer istatistiklerin de standart hataları vardır.
Hipotez Testi¶
Peki Merkezi Limit Teoremi bize nasıl yardımcı olacak? Teorem, ele alınan bir örneğin karşılaştırma yapılan bir popülasyonu temsil edip etmediği hipotezini test etmemizi, bunun için normal dağılımın parametrelerini kullanmamıza olanak sağlar. Bunun için örneğin ortalama değerini belirleyip, bu örneğin karşılaştırma yapılan popülasyondan gelip gelmediğini tahmin etmek için örneklem dağılımı ile karşılaştırabiliriz. Hipotez testinin belirli kuralları olup, öncelikle testin temellerini anlamaya ihtiyaç vardır.
Herhangi bir bilimsel problemin çözümünde öncelikle bir hipotez geliştirilir. Hipotez, bir problemin çözümüne elde az sayıda kanıt ve çalışma varken yapılan ve daha ileri araştırma için bir başlangıç noktası oluşturan öneridir.
Sıfır hipotezi ($H_0$), bir öneriyi test etmek üzere, gözlenen bir olayın sadece rastgele süreçler ile oluştuğunu, örnekleme ya da deneysel hatalardan kaynaklandığını öne süren hipotezdir. Gözleme ilişkin alternatif hipotezin ($H_1$) yani gözlenen olgunun rastgele süreçlerle oluşmadığının ve olgunun parametreleri arasında bir korelasyon bulunduğu fikrinin geçerliliğinin test edilmesi için kullanılır.
Sıfır hipotezinin yanlışlanamaması durumunda gözlenen olayın sadece rastgele süreçlerden kaynaklandığı (ya da sıfır hipotezinin geçerli olduğu) kabul edilir. Sıfır hipotezinin yanlışlanması durumunda ise alternatif hipotezin doğruluğu kanıtlanmış olmaz. Ancak gözlenen olgunun sadece rastgele süreçlerden (ya da sıfır hipotezinin öngördüğü süreçlerden) kaynaklanmadığı sonucuna varılır.
Sıfır hipotezinin yanlışlanması için, alternatif hipotezin gerçekleşebilme olasılığının, rastgele süreçler ile gerçekleşme ya da sıfır hipotezinin ilgilendiği dağılıma göre benzer bir olayın gözlenebilme olalsılığından anlamlı bir mertebede yüksek olması gerekir. Örneğin; bir bitkiyi sulamanın, bitkinin büyüme hızıyla ilişkili olduğunu söyleyen bir alternatif hipotezin kabul edilebilmesi için, bitkinin büyüme hızıyla sulama arasında bir ilişki olmadığını söyleyen sıfır hipotezinin yanlışlanması gerekir. Daha radikal bir örnek olarak; piramitleri uzaylıların inşa ettiğini iddia eden alternatif hipotezin kabul edilebilmesi için öncelikle, piramitleri uzaylıların inşa etmediğini iddia eden sıfır hipotezinin yanlışlanması gerekir. Tabi ki bu durumda piramitleri uzaylılıarın inşa ettiğine ilişkin doğrudan bir kanıtın da bulunması icap eder.
Örnek: CoVid 19 ilacı¶
Diyelim ki CoVid-19 hastalığı için bir ilaç önerisi var. İlacın başarısını test etmek için $n$ bireyi rastgele seçerek bir örneklem oluşturuyor ve bu bireylere ilacı veriyoruz. Diyelim ki bu $n$ bireyin $k$ tanesinin bir süre sonra (örneğin 2 hafta) yapılan testleri (ve diğer klinikleri) negatif sonuç veriyor ve bu $k$ bireyi "sağlıklı" olarak değerlendiriyoruz. Şimdi ilacın işe yarayıp yaramadığına yönelik hipotez testinin nasıl yapılacağına bakalım.
$H_0$ (Sıfır hipotezi): İLacın hiçbir etkisi yoktur ve sağlıklı olan $k$ birey hiçbir şey yapılmasa da hastalığı belirlenen sürede (2 hafta) kapmayacak bireylerdir.
$H_1$ (Alternatif hipotez): Aşı bireylerin hastalıktan etkilenmesini engellemektedir.
Test edilmesi gereken hipotez $H_0$ hipotezidir. Eğer bu hipotez doğruysa, aşılanan $n$ bireydeki $k$ negatif sayısının (örneklem büyüklüğüne oranının), tüm toplumdaki $K$ negatif sayısına (popülasyona oranına) benzer olması gerekir.
Diyelim ki hastalığı kapma olasılığı aşı vs. gibi bir engelleyici olmadan %25 olsun (p = 0.25). Bu durumda da kapmama olasılığı (q = 1 - p = 0.75) %75 olur ve bu deney iki olasılığın olduğu bir Bernoulli deneyidir ve dağılım da Bernoulli Dağılımı'na uyar.
Diyelim ki örneklemimiz 10000 birey ile sınırlı (n = 10000). Bu durumda sağlıklı birey $k$ sayısı 2 hafta sonra 10000 x 0.75 = 7500 çıkarsa (Bernoulli dağılımının ortalama değeri) bunun tamamen rastgele olduğunu, ilacın bir etkisi olmadığını söyleyebiliriz. Zira hiçbir şey yapılmasa da hastalığı kapmama olasılığı zaten %75'tir. Ancak bu durumda hangi sayıda sağlıklı birey bulursak $H_0$ hipotezini reddetmeliyiz (ilacın bir etkisi olmadığı sonucuna varmalıyız) gibi bir seçimle karşılaşırız. Zira 7500 değil de 7440 sağlıklı birey (%74.4) ya da 7590 (%75.9) sağlıklı birey bulmamız sadece örneklemimizin küçüklüğünden kaynaklanıyor olabilir mi?
Burada 7500'ün her iki tarafından belirli bir standart sapma ($\sigma$) değerini belirleyip, eğer deneydeki sağlıklı birey sayısı ortalamanın (7500) örneğin $2~\sigma$ ya da $2.5~\sigma$ içinde kalıyorsa $H_0$'ı kabul etmek, aksi takdirde reddetmek iyi bir fikir olabilir. İşte burada merkezi limit teoreminin temel yaklaşımını hatırlayabiliriz. Her ne kadar ilgilendiğimiz dağılım bir Bernoulli dağılımıysa da yeterince büyük örneklemlerle çalışıldığı vakit bu dağılımın normal dağılıma yakınsayacağını biliyoruz. Dolayısı ile normal dağılımın parametreleri ve yaklaşımıyla hareket edebiliriz!
Bir Bernoulli dağılımının standart sapması $\sigma = \sqrt{n~p~q}$ ile verilir. Bu durumda örneğimiz için standart sapma değeri $\sigma = \sqrt{10000~0.25~0.75} = 43.30$ olarak bulunur. Burada iki konuya değinmek gerekir:
1) Çalışmamızın daha "güvenilir" olması için ortalamadan kaç standart sapma ($\sigma$) uzaklığı $H_0$'ı red ya da kabul etmek için kriter yapmalıyız?
2) "Yeterince büyük örneklem" nedir, bir ölçüsü var mıdır?
Önceliklle ikinci sorunun cevabının popülasyonun büyüklüğüne bağlı olduğunu, örneklemin bazı problemlerde sadece niceliğinin (büyüklüğünün) değil de aynı zamanda niteliğinin (içerdiği örneklerin popülasyon niteliğini ne kadar yansıtıyor olduğunun) de dikkate alınması gerektiğini söylemek gerekir.
Birinci sorunun cevabı ise "Güven Aralığı" (ing. Confidence Interval) ya da "Güven Düzeyi" (ing. Confidence Level) kavramlarıyla verildiğini belirterek bu kavramları açmak gerekir.
import scipy.stats as st
import numpy as np
n = 10000
p = 0.25
q = 0.75
k_test = st.norm.ppf(0.95,loc=7500,scale=np.sqrt(n*p*q))
print(k_test)
stsapma = np.sqrt(n*p*q)
z = st.norm.ppf(0.95, loc=0, scale=1)
print("z = {:.6f}, sigma*z = {:.6f}".format(z,z*stsapma))
Güven Aralığı ve Güven Düzeyi¶
Güven aralığı, bir örnek dağılımın ortalama değerinin, ana dağılımın ortalama değerinden hangi olasılık mertebesi dahilinde uzak olduğunu gösteren aralıktır. Doğa bilimlerinde belirsizlik ölçütü olarak genellikle standart sapmayı kullanmak yeterlidir. Ekonomi ve siyaset bilimi gibi bazı başka disiplinlerde standart sapmayı vermek yerine güven aralığı (ing. confidence interval) ya da genellikle yüzde biriminde ifade edilen güven düzeyi (ing. confidence level) vermek tercih edilir.
Örneğin bir parametre için yapılan bir dizi ölçümün sonucu $101.25 \pm 0.01$ olarak verilmiş olsun. Aksi söylenmediği (örneğin bu hatanın ölçüm aletinin limiti olduğu gibi) sürece bir doğa bilimci bu belirsilziiği bir standart sapma olarak yorumlar ($\sigma = 0.01$). Ancak 2 standart sapma ($2~\sigma$) kullanarak ölçümün $\% 95$ güven düzeyinde $101.25$ sonucunu verdiğini söylemek de aynı içeriği taşır. Zira normal olduğu kabul edilen bir dağılımda %95 güven düzeyi de yaklaşık olarak $\pm 2\sigma$’ya (daha yaklaşık bir değer olarak $1.96~\sigma$) karşılık gelir. Benzer şekilde ölçüm sonucunun $(101.23 , 101.27)$ %95’lik güven aralığında olduğu da söylenebilir.
%95’lik güven aralığı, deney/gözlem tekrarlanmaya devam edilirse tekrarların %95’inde, gözlenen değerlerin bulunan güven aralığında çıkacağı anlamına gelir.
Örnek: CoVid-19 ilacı¶
CoVid-19 ilacı önerisi örneğinde standart sapmayı Bernoulli Dağılımı'ndan hareketle belirlemiştik. İlacın hiçbir etki yapmadığı, ilaç uygulamasının 2 hafta sonunda sağlıklı bireylerin tamamen rastlantısal olarak sağlıklı kaldıklarını ifade eden $H_0$ sıfır hipotezini reddetmek için $\%95$'lik bir güven düzeyi belirlemiş olalım. Bu durumda
$$ \mu \pm 2~\sigma = 7500 \pm 1.645 x 43.30 = 7500 + 71.22 $$dahilinde bir güven aralığı oluşturabiliriz. 2 hafta sonunda sağlıklı birey sayısını 7572'den büyük bulursak $H_0$'ı reddedebiliriz. Yani "ilacın hiçbir etkisi yoktur" önerisini reddetmiş oluruz! Bu alternatif hipotezi kabul ettiğimiz (yani ilacın etkili olduğu) anlamına gelmez ama onu destekleyici bir kanıt oluşturur.
Örnek: Gaia Paralaksları¶
Gaia uzay teleskobu gökcisimlerinin hassas konum ölçümlerini yapmak üzere uzaya gönderilmiştir. Teleskop, galaksimiz içindeki yıldızların da paralaks ölçümlerini defalarca yaparak uzaklıklarının hassas bir şekilde belirlenmesini sağlamaktadır.
Bir yıldızın paralaks ölçümü 1000 defa yapılıyor ve uzaklğı parsek cinsinden hesaplandığında elde edilen ortalama uzaklık değeri ($\mu_d$) ve standart sapması ($\sigma_d$) $d = 210 \pm 5$ pc olarak veriliyor. %95 güven seviyesine karşılık gelen aralığı bulunmak isteniyor olsun.
Çözüm: %95’lik güvenilirlik seviyesine karşılık gelen $z$ değeri için standart normal dağılım tablolarına ya da grafiklerine bakılır. Bu değer scipy.stats.norm.interval fonksiyonuyla doğrudan elde edilebilir ya da $p = 0.95$ için aşağıdaki formülden yararlanılarak hesaplanan $z$ değeri tablodan alınabilir. Daha sonra,
ifadesinden hareketle $x$ değişkeninin %95 olasılıkla içinde bulunduğu güven aralığı tesis edilir.
from scipy import stats as st
p = 0.95
z = st.norm.interval(p)
print("%{:.2f} olasiliga karsilik gelen z-değeri: {:.2f} 'dir.".
format(p*100, z[1]))
Görüldüğü üzere $z$-değeri %95'lik güven aralığı için 1.96 olarak verilmektedir. Bu durumda güven aralığı aşağıdaki şekilde tesis edilebilir.
$$ z = \frac{|x - \mu|}{\sigma} \Rightarrow x = \mu \pm z~\sigma \Rightarrow x = 210 \pm 1.96~x~5.0 = 210 \pm 9.8~pc$$Bir başka deyişle, 1000 kez paralaks ölçümü yapılan bu yıldızın uzaklığı %95 güven düzeyinde $(200.2 , 219.8)$ pc aralığındadır.
Aynı sonuca scipy.stats.norm.interval fonksiyonu aşağıdaki şekilde kullaılnarak da ulaşılabilir.
from scipy import stats as st
p = 0.95
mu = 210.0
sigma = 5.0
aralik = st.norm.interval(p,loc=mu, scale=sigma)
print("Yildizin uzakligi icin %{:.2f}'lik guven araligi ({:.2f}, {:.2f}) pc'tir.".\
format(p*100, aralik[0], aralik[1]))
Görüldüğü üzere yeterince fazla ölçüm yapıldığında ölçüm sonuçlarının normal dağıldığını varsayarak, normal dağılımın parametreleriyle (ortalama ve standart sapma) bir güven aralığı oluşturulmuştur. Oysa ki tek bir ölçüm (ya da az sayıda ölçüm) söz konusu olduğunda ölçüm hataları normal (ya da Gaussyen) dağılmaz, Poisson Dağılımı'na (ya da genelleştirilmiş hali olan Drichlet Dağılımı'na) uyar. Ancak Merkezi Limit Teoremi gereğince yeterince büyük bir örneklem söz konusu olduğunda, rastgele bir değişkenin değerinin dağılımı Normal Dağılım'a yakınsar. Bu durumda da normal dağılım yaklaşımından hareketle analiz yapılabilir.
Diyelim ki bu yıldızın uzaklığı bir başka yöntemle (örneğin çift yıldız gözlemleriyle oluşturulan kalibrasyondan hareketle ya da HIPPARCOS uzay teleskobu ölçümleriyle) belirlenmiş olsun. Bu ölçümlerin hangi güvenilirlik düzeyinde eşit kabul edileceğine karar verildikten sonra sıfır hipotezi ($H_0$) ve alternatif hipotez ($H_1$) aşağıdaki şekilde oluşturulabilir.
$H_0$: Yildizin Gaia uzakligi cift yildiz gozlemlerinden belilrlenen kalibrasyonla uyumlu degildir.
$H_1$: Yildizin Gaia uzakligi cift yildiz gozlemlerinden belilrlenen kalibrasyonla uyumludur.
Bu tür bir karşılaştırmanın nasıl yapılacağını biraz sonraya bırakarak hipotez testlerinde yapılabilecek olası hataları görelim.
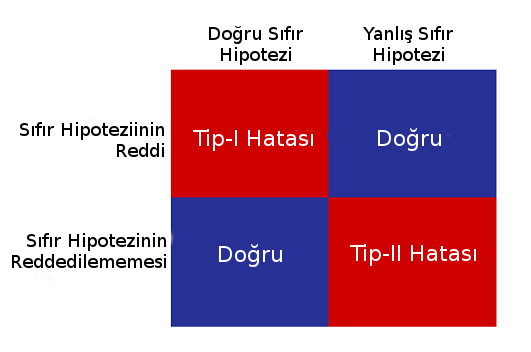
Hipotez Testinde Tip I ve Tip II Hataları¶
Tip-I Hata (ing. Type-I Error): Sıfır hipotezinin ($H_0$) doğru olmasına karşın reddedilmesiyle oluşan hatadır. Özellikle örnek sayısının azlığından kaynaklanabilir.
Tip-II Hata (ing. Type-II Error): Sıfır hipotezini ($H_0$) yanlışlığına rağmen kabul edilmesiyle oluşan hatadır.
İstatistiksel Anlamlılık Seviyesi¶
İstatistiksel anlamlılık, bir örneklemden türetilen bir istatistiğin o örneklemin alındığı popülasyondaki bir olguyu ne düzeyde (hangi olasılıkla) temsil ettiğinin ölçüsüdür. Örneğin "Bir popülasyondan alınan bir örneğin ortalamasının, o örneğin popülasyonu temsil etmediği ve şans eseri oluştuğu (örneklem hatası) kanısına bu iki ortalamada hangi düzeyde bir fark olursa varılmalıdır?" sorusunun cevabı araştırmacı tarafından belirlenen istatistiki anlamlılık seviyesiyle karşılaştırma yapılarak verilir. Eğer ulaşılan sonucun (örneğin iki ortalama arası farkın) olasılığı seçilen anlamlılık seviyesinden küçükse bu sonucun istatistiksel olarak anlamlı olduğu ve şans eseri (örneklem hatası nedeniyle) oluşma ihtimalinin istatistiksel anlamlılık seviyesiyle izin verilenden daha küçük olduğu sonucu çıkar.
Gözlenen olayın rastgele süreçlerden meydana gelip gelmediği test edilmek istendiği için, olayın gerçekleşme ihtimali bir normal dağılım kullanılarak incelenir. Eğer olaya ilişkin dağılımın rastgele dağılım olmadığı biliniyorsa ilgili dağılım kullanlabilir. Ancak yeterli sayıda örnek dağılım elemanı bulunuyorsa merkezi limit teoremi gereğince normal dağılım varsayımı, bulunmuyorsa normal dağılım yerine, düşük serbestlik derecelerine daha duyarlı olan t-dağılımı varsayımı yapılabilir.
Istatistiksel anlamlılığın belirlenebilmesi için kullanılan kritik değer $\alpha$, bir olasılık değeri anlamındadır. Farklı bilim dallarında farklı değerler kabul görebilmektedir. Gözlenen olgunun rastgeleliğinin büyük oranda beklenir olduğu durumda daha küçük olasılık değerleri verilmesi uygun olur.
İstatistiki anlamlılık seviyesi (ing. statistical significance), toplam olasılık olan $1$’den güven seviyesinin farkıdır.
Sıfır hipotezi ($H_0$) doğru ise ve gözlemsel verinin ya da ilgili parametrenin normal dağılım sergilemesi bekleniyorsa, normal dağılımca beklenen en olası değer ortalama değerdir. Bu durumda kritik olasılık değeri ($\alpha$) belirlendiği takdirde, kritik değere göre ortalamaya daha yakın olan toplam olasılık değerleri sıfır hipotezinin reddedilememesi anlamına gelir. Bu durumda sıfır hipotezi $1- \alpha$ güven aralığında reddedilememiş olur.
[CoVid-19 aşısı](#Örnek:-CoVid-19-aşısı) örneğinde güven düzeyinin %95 olarak belirlenmesi durumunda istatistik anlamlılık seviyesi $\alpha = 1 - 0.95 = 0.05$ 'tir. 1 yıl süren aşılama sürecinin sonunda bu düzeyin üzerinde bir iyileşme (ki bunun 7572 hastaya denk geldiğini görmüştük) istatistiki olarak anlamlı bir sonuç bulunduğu değerlendirmesi yapılabilir. Bu da alternatif hipotez $H_1$ için istatistiki olarak anlamlı bir kanıta ulaşıldığı anlamına gelir. Ancak bu $H_1$'in kabul edildiği anlamına da gelmez.
[Gaia paralaksları](#Örnek:-Gaia-Paralaksları) örneğinde;
$H_0$: Gözlenmiş çift yıldızlar üzerinden belirlediğiniz bir korelasyon %95 güven düzeyinde Gaia ölçümüyle ($\mu = 210~pc$) uyumludur.
şeklinde ifade edilen bir sıfır hipotezini yanlışlamanız için kalibrasyonunuzun $\alpha = 1 - 0.95 = 0.05$ istatistiki anlamlılık seviyesinin karşılık geldiği $9.8~pc$ değerinin ötesinde bir değer (200.2 pc'ten küçük ya da 219.8 pc'ten büyük) bir uzaklık vermesi gerekir. Bu durumda kalibrasyonunuzun Gaia ölçümleriyle uyumlu olmadığını ifade eden $H_1$ alternatif hipotezine ilişkin bir kanıta ulaşmış olursunuz.
p Değeri¶
p-değeri (ing. probability value: p-value), sıfır hipotezinin ($H_0$) doğru kabul edilmesi durumunda gözlenen bir sonucun ne kadar olası olası olduğunu ifade eder. Sıfır hipotezinin ($H_0$) doğru olması durumundaki olasılık belirlendiği için koşullu bir olasılıktır. Özünde bu değer bir hipotezin doğru olduğu kabulü altında herhangi bir istatistiğin tamamen şans eseri olarak elde edilmesi olasılığını verir. Burada şanstan kasıt, rastgele seçimle örneklem oluşturulurken bu sonucu verecek örneklerin (verilerin) seçilmiş olmasıdır (örneklem hatası, ing. sampling error).
p-değeri belirlenen bir istatistiki anlamlılık derecesinden (ing. statistical significance: $\alpha$) daha küçükse sıfır hipotezi ($H_0$) reddedilir. Çünkü elde edilen sonuç belirlenen düzeyde istatistiksel olarak anlamlıdır. Sıfır hipotezi doğru iken bu sonucun elde edilmesi tamamen şans eseri (örnekleme hatasıyla) olarak da olasıdır. Ancak bu olasılık istatistiksel anlamlılıkla izin verilenden daha azdır. Bu durumda alternatif hipotez ($H_1$) için bir kanıt elde edilmiş olunur. Eğer p-değeri belirlenen istatistiki anlamlılılk derecesinden büyükse $H_0$ reddedilemez (bu kabul edildiği anlamına gelmez!). Çünkü sonuç belirlenen düzeyde istatistiksel olarak anlamlı değildir. Bu sonucun sıfır hipotezinin doğru olması durumunda şans eseri elde edilmiş olma ihtimali belirlenen istatistiksel anlamlılık seviyesinden büyüktür ki zaten sıfır hipotezi rastgele seçilen bir örneğin doğrulaması üzerine kuruludur.
Örneğin p-değeri $0.03$ olarak hesaplanıyor ancak belirlenen istatistiksel anlamlılık değeri $\alpha = 0.05$ ise, bu $H_0$'ın doğru olması durumunda elde edilen sonucun tamamen şans eseri elde edilme olasılığının $\%5$’ten küçük bir olasılığa sahip olduğu ($\%3$) anlamına gelir. Bu nedenle $H_0$ reddedilir. Bir başka deyişle, hesaplanan değer gözlenen olgunun örneklem hatasıyla oluşma ihtimalini $\%3$ olarak belirlediği için $H_0$ reddedilir. Ancak p-değeri (örneğin biraz sonra göreceğimiz t-testi ile) 0.1 olarak hesaplanırsa bu böyle bir örneklemin $H_0$’ın doğru olması durumunda $\%10$ ($> \alpha = 0.05$) ihtimalle rastgele herhangi bir örneklem için elde edilebileceğni gösterir ki bu durumda $H_0$ reddedilemez.
Örnek: p Değeri¶
Diyelim ki açık yıldız kümelerinin içerdiği yıldızların %25’inin G tayf türünden daha sıcak yıldızları içerdiği gibi bir iddia var ve biz de bir açık yıldız kümesi gözleyerek bu iddiayı test etmek istiyoruz.
Bu durumda sıfır hipotezi
- $H_0$: $\mu = 0.25$,
alternatif hipotez ise
- $H_1$: $\mu \neq 0.25$
olarak belirlenebilir.
Şimdi yapmamız gereken gözlediğimiz kümedeki G tayf türünden daha sıcak yıldızları saymak (diyelim ki 120 yıldızdan 40’ı böyle yıldızlar olsun) ve $H_0$ ‘ın doğru olduğu kabulü altında bu gözlem sonucunun tamamen şans eseri elde edilip, edilemeyeceğini bulmak!
Bu deney yine bir Bernoulli deneyidir. Zira kümdede ele alınan bir yıldız ya G tayf türünden daha sıcaktır. ya da değildir. Bu durumda standart sapma $\sigma = \sqrt{n p q} = \sqrt{120~0.25~(1-0.25)} = 4.74$ olarak bulunur. %25 G tayf türünden daha sıcak yıldız bulma olasılığı ise $\mu = 0.25~x~120 = 30$ yıldıza karşılık gelir.
$$ z = \frac{x - \mu}{\sigma} = \frac{40 - 30}{120~0.25~0.75} = 2.108 \sim 2.11$$Şimdi iş bu z-değerinin karşılık geldiği p-değerini hesaplamaktır. Bu değer bir standart normal dağılımı tablosundan (z-tablosu) alınabileceği gibi scipy.stats.norm fonksiyonlarıdan cdf() da bu amçla kullanılabilir. Ancak cdf() (1 - p) değerini vereceği için, doğrudan p-değerini veren sf() fonksiyonu (ing. survival function) da tercih edilebilir.
from scipy import stats as st
z = 2.108
p = st.norm.sf(z)
print("z = {:.2f} degeri p-degeri = {:.4f}'e karsilik gelir".\
format(z, p))
olasilik = st.norm.cdf(z)
print("z = {:.2f} degerinin karsilik geldigi olasilik = %{:.2f}'tir.".\
format(z, 100*olasilik))
$z = 2.11$’e karşılık gelen p-değeri $p = 0.0175$ bulunur. Yani bu örneğin bu popülasyondan örnekleme hatasıyla türetilmiş olma olasılığı %1.75 olup istatistiksel anlamlılığın $\alpha = 0.05$ seçilmesi durumunda $p = 0.0175 < \alpha$ olduğu için $H_0$ reddedilir. Yani, ele alınan örnek iddianın doğru kabul edilmesi durumunda istatistiksel anlamlılık seviyesi dahilinde tüm açık yıldız kümeleri popülasyonlarından rastgele bir seçimle türetilmiş olabilir ama bu ihtimal "göreli olarak (istatistiksel olarak anlamlı sayılacak düzeye göre) düşüktür". Bu nedenle de elimizdeki yıldız grubu (örneklem) tüm açık yıldız kümelerindeki G-tayf türünden yıldızların (popülasyon) oranının $\%25$ olduğu iddiasıyla çelişmektedir! Ama biz evrendeki tüm açık yıldız kümelerini gözleyemeyiz ve hiçbir zaman da gözleyemeyeceğiz! O yüzden, $H_1$ kabul edilmiş de değildir ama o yönde bir kanıt elde edilmiştir. Bu sonuç daha fazla örnekle ya da istatistiksel anlamlılık seviyesi değiştirilerek, daha yüksek bir güven düzeyinde konuşmak istendiğinde yanlışlanabilir. Dolayısı ile bu güven düzeyinde $H_0$'ı reddetmiş olmakla şöyle bir yanlış yapıyor olabiliriz: Çok küçük bir ihtimalle de olsa bu veri $H_0$ (tüm yıldızların %25'inin G-tayf türünden sıcak yıldızlar olduğu) doğru olduğu halde örnekleme hatasıyla ("talihsizlik!") oluşmuş da olabilir! Yani 120 yıldızlık örneğimizde 40 yıldızın G-tayf türünden olması bu önerme doğru olduğu halde örneklem hatası (şans kaynaklı) nedeniyle düşük ihtimaldir! Bu durumda Tip-I Hatası yapılmış olur.
Ancak %99'luk güvenlik düzeyine denk gelen $\alpha = 0.01$ seçilseydi $p > \alpha$ olduğu için $H_0$ reddedilemezdi. Bir başka deyişle, elimizdeki örnek açık yıldız kümelerindeki yıldızların %25’inin G tayf türünden daha sıcak yıldızları barındırdığı iddiasını $\alpha = 0.01$ istatistiksel anlamlılık ya da $\%99$ güven seviyesinde reddetmez; çünkü bu örneklem, $H_0$'ın doğru olması durumunda, istediğimiz ya da izin verdiğimiz anlamlılık seviyesinden (%1) daha yüksek bir olasılığa (%1.75) sahiptir. Yine benzer şekilde, bu önermeyi reddetmemekle bir hata yapıyor olabiliriz. Yani $H_0$ hipotezi reddedilmediği halde, onun örneklemimiz için öngördüğü sayıya ($30$) istatistiksel anlamlılığın izin verdiği kadar yakın sayıda sıcak yıldız içeren bir açık kümeyi tamamen şans eseri (örneklem hatası sonucu) seçmiş de olabiliriz. Yani $H_0$ doğru olmayabilir ama talihsizlik eseri seçtiğimiz örnek onun öngördüğüne yakın bir sonuç vermiştir. Bu durumda da Tip-II Hatası yapılmış olur.
Şimdi seçtiğimiz istatistiksel anlamlılık seviyesinin ($\alpha = \%1 = 0.01$)'in karşılık geldiği yıldız sayılarına bakalım. Elimizdeki örnekte kaç yıldızdan daha az ya da daha çok sayıda G-tayf türünden daha sıcak yıldız olması $H_0$'ı reddetmemize yol açar, çünkü belirlediğimiz istatistiksel anlamlılık seviyesinde $H_0$'ın öngördüğünden daha az ya da daha çok G-tayt türünden sıcak yıldız içerir? Bu iki yönlü bir testtir. İstatistiksel anlamlılık nihayetinde bir olasılık olduğu ve belirleyeceğimiz yıldız sayılarından az ve çok yıldız içerme olasılıkları toplanacağı için, bu olasılık, eğrinin altında ortalamadan ($30$) her iki yönde belirlemek istediğimiz sayıların dışında kalan alandır. Bu sayıları scipy.stats.norm.interval() fonksiyonu ile belirleyebiliriz. Ancak bu fonksiyonun eğrinin $H_0$'ın kabul edildiği alanı veren uç değerleri döndürdüğüne dikkat edilmelidir. Bu nedenle istenen $\alpha$ değerinin karşılık geldiği uç noktalar için, o olasılığın 1'den farkı alınarak interval() fonksiyonuna sağlanması gerekir. Bu değer aynı zamanda güven düzeyini ifade eder.
### Secilen istatistiksel anlam seviyesinin karsilik geldigi
# yildiz sayilari
alpha = 0.01
olasilik = 1-alpha
sayi = st.norm.interval(olasilik,loc=30,scale=4.74)
print("alpha = {:.2f} degerinin karsilik geldigi yildiz sayilari {:.2f} ve {:.2f}'dir.".\
format(alpha, sayi[0], sayi[1]))
Görüldüğü gibi, açık yıldız kümemizin, $H_0$ doğru iken belirlediğimiz istatistiksel anlamlılık seviyesinde (%1) 42.21'den (42) fazla, 17.79'dan (18) az sayıda G-tayf türünden sıcak yıldızı şans eseri (örnekleme hatasıyla) içerme olasılığı %1'in altında olmalıdır. Eğer sözgelimi bizim incelediğimiz kümede 45 böyle yıldız olsaydı, "rastgele bir seçimde bu kadar yıldız içeren bir kümeye denk gelme olasılığımız %1'in altında o nedenle $H_0$ doğru olamaz!" derdik. Oysa ki bizim kümemizde 40 tane bu tür yıldız var. O nedenle $H_0$ bu anlamlılık seviyesinde reddedilemez!
Oysa ki $H_0$'ı reddettiğimiz ilk anlamlılık seviyesi olan $\alpha = \%5 = 0.05$ için bu sayıları hesaplasak;
### Secilen istatistiksel anlam seviyesinin karsilik geldigi
# yildiz sayilari
alpha = 0.05
olasilik = 1-alpha
sayi = st.norm.interval(olasilik,loc=30,scale=4.74)
print("alpha = {:.2f} degerinin karsilik geldigi yildiz sayilari {:.2f} ve {:.2f}'dir.".\
format(alpha, sayi[0], sayi[1]))
elde ederdik. Görüldüğü gibi bu anlamlılık seviyesinde $39.29$'dan daha fazla sıcak yıldız içeren bir açık kümeyi tamamen şans eseri oluşturma olasılığı $\%5$. Yani $H_0$ doğruyken rastgele seçtiğimiz bir kümenin 40 yıldız içeren bir küme olma olasılığı bundan daha az.
t Dağılımı¶
Tüm parametrelerin değerleri Gaussian olasılık dağılımına uygun dağılmayabilir. Bazı parametreler, Gaussian dağılımına uyuyor gibi görünse de ortalamadan uzak değerlerinin olaslıkları Gaussian dağılımla öngörülenden yüksek bulunablir. Önemli bir başka durum yeterince örnek sayısının olmadığı durumdur ki bu durumda ortalama ve standart sapma çok iyi belirlenmememiş olabilir. Bu durumlarda parametre değerlerinin olasılık dağılımı için t-dağılımını (ing. Student's t-distribution) kullanmak daha iyi bir seçenektir.
$t$-istatistiği, $x$ değerinin, örneğin ortalama değeri olan $\bar{x}$ değerinden kaç standart sapma ($s$) uzaklıkta olduğunu belirler ve aşağıdaki şekilde ifade edilir.
$$ t = \frac{|x - \bar{x}|}{s} $$Bu durumda $t$-istatistiği için olasılık dağılımı
$$ P(t,\nu) = \frac{1}{\sqrt{\nu~\pi}} \frac{\Gamma[(\nu + 1) / 2]}{\Gamma(\nu / 2)} (1 + \frac{t^2}{\nu})^{-(\nu + 1)/2} $$dir. Burada $\nu$ serbestlik derecesini gösterir ve $\bar{x}$ $N$ bağımsız ölçümün ortalamasıysa $\nu = N - 1$ ile verilir.
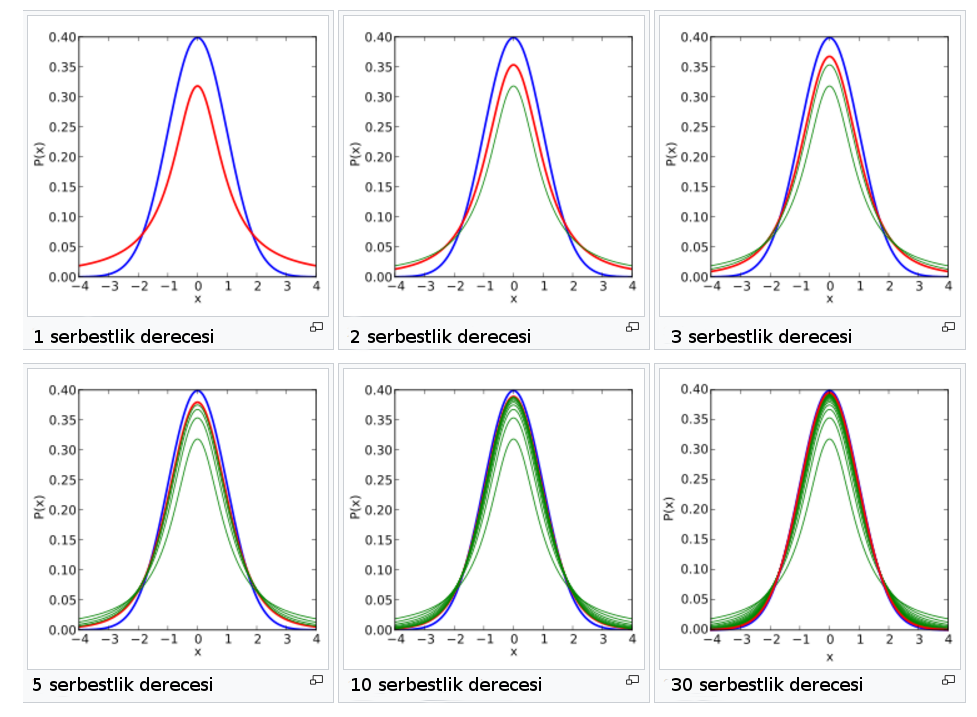
Aşağıdaki görselde, serbestlik derecesinin değişmesi ile t-dağılımının değişimi görülmektedir. Mavi ile gösterilen eğri standart normal dağılımdır. 1 serbestlik derecesine sahip olan t-dağılımında görüleceği üzere, $t$-dağılımı, daha geniş kanatlara sahiptir. Bu normal dağılımın ortalama değerinden daha uzakta ortalama değerlerin bulunma olasılığının normal dağılıma göre daha fazla olduğunu göstermektedir; ki az sayıda ölçüm söz konusu olduğunda bu yaklaşım daha gerçekçidir. Her bir serbestlik derecesi için verilen dağılımda önceki serbestlik dereceleri için t-dağılımı yeşille, verilen serbestlik derecesi için kırmızıyla gösterilmektedir.
Serbestlik derecesi arttıkça ya da başka bir deyişle örneklem büyüdükçe, t-dağılımı da normal dağılıma yakınsamaktadır. Bunun sonucu olarak, örneklemdeki eleman sayısının az olması durumunda t-dağılımının kullanılması, normal dağılımın kullanılmasından daha uygun olmaktadır.
Örnek: Gaia Paralaksları t dağılımı Yaklaşımı¶
Henüz Gaia görevinin ancak belirli bir bölümünü (EDR-3) tamamlamış durumdadır ve aynı yıldızın paralaks ölçümünü belirli kez yapabilmiştir. Daha önceki örnekte gördüğümüz yıldızın 9 paralaks ölçümü yapılmış ve uzaklğı parsek cinsinden hesaplandığında elde edilen ortalama uzaklık değeri ($\bar{x}$) ve belirsizliği ($s$) $210 \pm 5 ~pc$ olarak veriliyor olsun. %95 güven seviyesine karşılık gelen aralığı bu kez $t- dağılımı$ kullanarak bulalım.
Bu kez ölçüm sayısı çok az olduğu ($N = 9$) için serbestlik derecesini dikkate alan t-dağılımı üzerinden bir güven aralığı tesis etmek istiyoruz. t-dağılımı için verilen kümülatif olasılık tablosundan %95 güven seviyesine $ν = 9 – 1 = 9 – 1 = 8$ serbestlik derecesi için karşılık gelen $t-istatistiği$ değeri $t = 2.3$’tür. Bu durumda;
$$ t = \frac{|x - \bar{x}|}{s} = 2.3 $$$$ t = \frac{|x - \bar{x}|}{s} = 2.3 \Rightarrow x = \bar{x} \pm t~s \Rightarrow x = 210 \pm 2.3~x~5 = 210 \pm 11.5~pc$$Bu durumda %95 güven seviyesine karşılık gelen aralık:
$$ x = (210 – 11.5, 210 + 11.5) = (198.5, 221.5) $$aralığıdır.
Aynı güven seviyesi için çok daha geniş olarak bulunan güven aralığı, t-dağılımının, Gaussyen (normal) dağılımın azımsadığı (ing. underestimate) uç değerlerin olasılıklarını daha büyük bulmasından kaynaklanmaktadır. Örnek sayısı az olduğu vakit, uç değerlerin olasılıklarının daha yüksek olması beklenebilir. Örnek sayısı artıp, serbestlik derecesi buna bağlı olarak yükseldikçe dağılım, Gaussyen’e yaklaşacaktır. Örneğin $\nu = 50$ serbestlik derecesi için $t \sim 2.0$ iken normal dağılımda güven aralığının hesaplanması için kullanılan $z$ parametresi de $z \sim 1.95$ değerini almaktadır. Oysa $N = 9$ olan örneğimizde $t = 2.3$ iken aynı güven aralığında $z = 1.96$’dır.
Aynı örneği Python'da scipy paketi fonksiyonlarından t-dağılımına ilişkin araçlar sunan scipy.stats.t() ile çözmeye çalışalım. Fonksiyon scipy kütüphanesinde yer alan, Ders-2b Dağılım Fonksiyonları'nda gördüğünüz diğer dağılım fonksiyonlarına benzer şekilde çalışır ve benzer metotlarla parametrelere sahiptir. t-dağılımı sürekli bir fonksiyondur bu nedenle süreksiz fonksiyonlardaki Olasılık Kütle Fonkskiyonu'nun (ing. Probability Mass Function, PMF) yerini Olasılık Yoğunluk Fonksiyonu (ing. Probability Density Function, PDF) alır. Aynı şekilde kümülatif olasılıklar da yoğunluk fonksiyonu (ing. Cumulative Density Function, CDF) ile ifade edilir.
Öncelikle problemimizin parametreleriyle %95'lik bir güven düzeyi için güven aralığı oluşturalım. Bu amaçla güven düzeyini (0.95) alpha parametresine (bu parametreinin ismi istatistiksel anlamlılığı simgeleyen $\alpha$ ile aynı olsa da güvenlik düzeyini doğrudan vermek gerektiğine dikkat ediniz), serbestlik derecesini ($\nu = N - 1 = 9 - 1 = 8$) stats.t fonksiyonunun df parametresine, ölçümlerin ortalamasını ($\mu = 210~pc$) loc parametresine, standart sapmasını ise scale parametresine vermeliyiz.
from scipy import stats as st
N = 9
xbar = 210 # pc
s = 5 # pc
gd = 0.95 # %95
guven_araligi = st.t.interval(alpha=gd, df=N-1, loc=xbar, scale=s)
print("%{:.1f}'lik guven araligi {:.1f} ile {:.1f} arasidir.".\
format(100*gd, guven_araligi[0], guven_araligi[1]))
t-dağılımına uyan bireysel ölçümleri (örneklemi) oluşturabilmek için rvs() fonksiyonunu kullanalım. Bunun için örneklem büyüklüğümüzü size parametresi ile $N = 9$'a, serbestlik derecesini df parametresi ile $\bar{x} = N - 1 = 8$'e, ortalama değeri loc parametresinden $\mu = 210~pc$ ve standart sapmayı da scale parametresinden $s = 5~pc$'e ayarlayalım.
from scipy import stats as sta
import numpy as np
# Ornegi tekrar ayni degerlerle uretebilmek icin
# seed edelim.
np.random.seed(53)
N = 9
xbar = 210 # pc
s = 5 # pc
paralakslar = st.t.rvs(df=N-1, loc=xbar, scale=s, size=N)
print(paralakslar)
Bir t-dağılımından verilen bu parametrelerle üretilen paralaks ölçümleri için doğal olarak ortalama ve standart sapma değerleri verilenlerle birebir aynı olmayacaktır. Zira işin içine rastgelelik katılmıştır. Ancak bu örnekte bireysel Gaia ölçümleri ürettiğimiz veri setimizi ($paralakslar$) kullanabiliriz. İstediğimiz parametrelerle bir t-dağılımından rastgele örneklem seçerek oluşturduğumuz bu t-dağılımına en iyi uyan olasılık yoğunluğu fonksiyonunu stats.t.fit fonksiyonuyla bulmaya çalışalım.
t_uyumlama = st.t.fit(paralakslar)
print("Ort: {:.2f}, St.Sapma: {:.2f}".\
format(t_uyumlama[1], t_uyumlama[2]))
İstenirse bu uyumlama (fit) fonksiyonunun parametrelerine karşılık gelen bir olasılık yoğunluk fonksiyonu (PDF) stats.t.pdf() fonksiyonu ile çizdirilebilir (sürekli mavi eğri). Bu fonksiyonunun yanı sıra karşılaştırma için başlangıçtaki parametrelerimize ($\mu = 210, \sigma = 5$) karşılık gelen bir t-dağılımı çizdirelim (süreksiz mavi eğri). Ayrıca uyumlama fonksiyonu ile elde ettiğimiz parametrelere karşılık gelen bir normal dağılım için de bir olasılık yoğunluk fonksiyonu çizdirelim (turuncu sürekli eğri).
from matplotlib import pyplot as plt
import numpy as np
%matplotlib inline
xbar_fit = t_uyumlama[1]
s_fit = t_uyumlama[2]
# Daha cok sayida nokta iceren bir x-ekseni tanimlayalim
x = np.linspace(200,225,50)
pdf_fit = st.t.pdf(x, df=8, loc=xbar_fit, scale=s_fit)
pdf_orj = st.t.pdf(x, df=8, loc=xbar, scale=s)
pdf_gauss = st.norm.pdf(x, loc=xbar_fit, scale=s_fit)
plt.hist(paralakslar, density=True, histtype='stepfilled', alpha=0.2)
plt.plot(x, pdf_fit, 'b-', label="Uyumlama")
plt.plot(x, pdf_orj, 'b--', label="Orjinal")
plt.plot(x, pdf_gauss, c="orange", ls="-", label="Normal")
plt.legend(loc="best")
plt.show()
Serbestlik Derecesi¶
Şu ana kadar pek çok kez kullandığımız ve daha önce de tanımladığımız serbestlik derecesi kavramını bu noktada hatırlamakta yarar var. Serbestlik derecesi değiştikçe t-dağılımının şekli (ve doğal olarak olasılıklar değiştiği) için t-tablolarına (ya da t-dağılımına dayanan scipy.stats.t fonksiyonlarına) başvurulurken serbestlik derecesi girdi parametresidir. Serbestlik derecesi (ing. Degree of Freedom, df ya da dof) temel olarak, formal tanımıyla) dinamik bir sistemin, üzerinde herhangi bir kısıtlamayı ihlal etmeden hareket edebileceği bağımsız yolların sayısı olarak tanımlanır ve sistemin eksiksiz olarak tanımlanabileceği bağımsız koordinatların sayısıdır. Bu bağlamda, serbestlik derecesi özet olarak bir sistemde bağımsız şekilde değişebilen değerlerin ya da niceliklerinin sayısıdır. Serbestlik derecesi, öncelikli olarak örnek dağılımın eleman sayısına (örnek büyüklüğüne) bağlıdır. Eleman sayısının fazla olması serbest olarak değişebilecek değerlerin sayısının da fazla olması anlamına gelir. Bir örnek dağılım için serbestlik derecesi; $dof = N -1$ ile veriliir. Burada serbestlik derecesi $dof$, örneklem büyüklüğü ise $N$’dir. Örnek dağılım, bir ana dağılımdan üretilmekte olduğu için, örnek dağılımın ortalama değeri, ana dağılımın ortalamasını temsil etmelidir. Bu durum serbestlik derecesinin 1 azalması anlamına gelir; bu nedenle serbestlik derecesi $N - 1$ olmuştur.
Aynı şekilde bir sistemin varyansı söz konusu olduğunda da serbestlik derecesi $dof = N - 1$'dir zira varyans, ortalamaya bağlı olarak hesaplanır.
Eğri uyumlamasında ise; $dof = N – m$ ile verilir. Burada $m$, uyumlamada kullanılan parametre sayısıdır. Uyumlamada kullanılan parametre sayısının fazla olması serbest olarak değişebilen değerlerin sayısının parametre sayısı kadar azalması anlamına gelir.
Model ve Artıkları¶
Bir bilimsel model gerçek bir olgunun fiziksel, kavramsal ya da matemetiksel olarak temsilidir. Bir modelin amacı bir olguyu daha kolay anlaşılır, yorumlanır, tanımlanır, nitel hale getirilebilir, görselleştirilebilir ve simüle edilebilir hale getirmektedir. Böylece bir model üzerinden geleceğe ilişkin tahminler de yapılabilir (ekstrapolasyon). Geçen ders gördüğümüz eğri uyumlama da gözlemsel (ya da deneysel) bir veri setine yapılan analitik bir modeldir.
Bir uyumlama işlemi sonunda, gözlemsel veri ile uyumlama eğrisinin değerleri arasındaki farklara artık (ing. residual) denir. Artıkların dağılımı ve gösterecekleri olası trendler, uyumlamada kullanılan yöntemin veya modelin ne kadar başarılı veya kabul edilebilir olduğunun bir ölçütü olarak kullanılabilir.
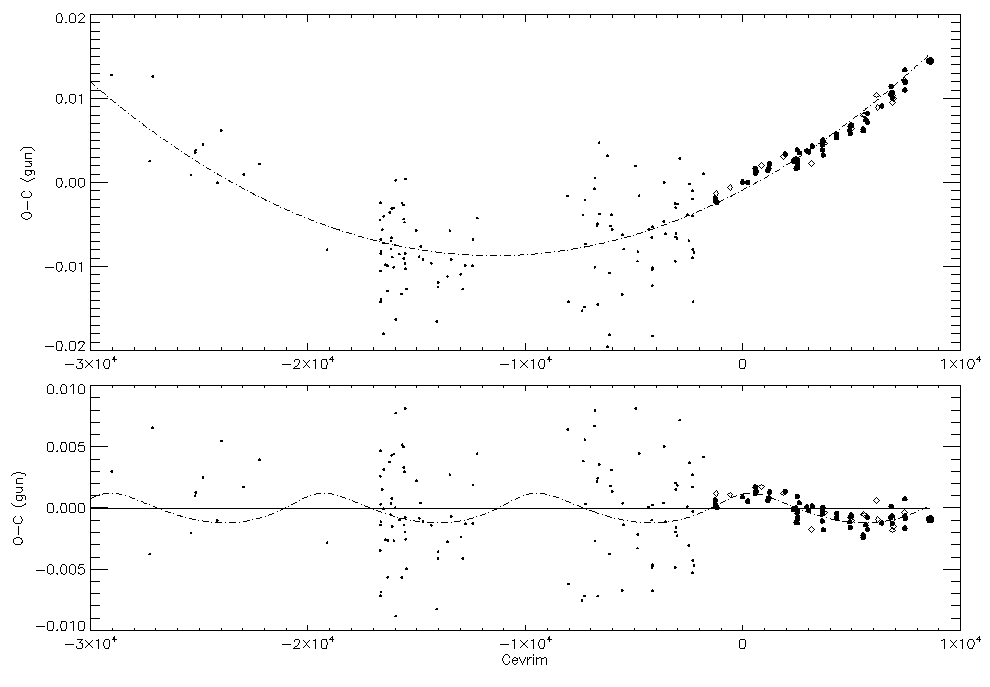
Aşağıdaki grafiğin üst panelinde HW Virgo yıldızının minimum zamanlarının (veri noktaları) değişimine yapılan bir parabol uyumlaması (kesikli eğri) görülmektedir. CCD gözlemleriyle elde edilen minimum zamanları daha büyük simgelerle, birinci minimumlar içi dolu, ikinci minimumlar içi boş çemberlerle gösterilmiştir. Alt panelde parabolik bu modelden artıklar görünmektedir. Bu panelde $y = 0$ doğrusu (sürekli doğru) parabole karşılık gelmektedir. Uyumlanan parabolün iki ucundan tutulup yatay bir doğru haline getirildiğini; bu sırada veri noktalarının da bu parabol modele olan uzaklıklarının bozulmadan taşındığnı düşünebilirsiniz. Veri noktalarının alt panelde modele göre bu şekildeki konumları, bir başka deyişle modelden farkları, artıkları verir. Yakın zamanda yapılan CCD gözlemleriyle elde edilen minimum zamanlara yapılan parabol modelden artıkların sinüsoidal bir değişim gösterdiği düşünülmüş, artık (Kepleryan) ikinci bir modelle uyumlanmıştır (kesikli eğri).
Artıklarda Değişen Varyans¶
Artıkların bir grafiğe aktarılarak görsel olarak incelenmesi model başarısının görsel olarak anlaşılması anlamında önemlidir. HW Vir örneğinde bu türden bir inceleme araştırmacıya artıkların yakın tarihli olanlarının sinüsoidal bir değişim gösteriyor olabileceği fikrini vermiştir. Ancak burada artıkların varyansının, geçmişte görsel ve fotokatlandırıcı tüpler ve fotoğraf plakları gibi dedektörlerle yapılan gözlemlerin duyarlılık yetersizliklerine karşılık yakın zamanlı gözlemlerin duyarlı CCD gözlemleri olması nedeniyle zaman içinde değiştiği görülmektedir. Artıklarda aşağıdaki örneklerdeki gibi değişen bir varyans sorunu söz konusu olduğu bu tür durumlarda doğrudan modelden artıkları incelemek yerine, normalize artıkları incelemek daha anlamlı olabilir.
Burada normalize artık, veri noktasının modele uzaklığının hatasına (ya da belirli bir bölümünün varyansına) bölümüyle tanımlanır. Böylece teknoloji yetersizlikleri, kötü hava koşulları gibi nedenlerle saçılması büyük olan veriyle daha ideal koşullarda, hatta uzaydan ya da kaliteli gözlem araçlarıyla ve büyük teleskoplarla yapılan gözlemleri birarada değerlendirmek mümkün olur.
Normalize artık ($R_i$), $y_i$ ölçüm değerlerini, $\hat{y}(x_i)$ o noktaya karşılık gelen model değerini, $\alpha_i$ ölçüm hatalarını göstermek üzere aşağıdaki şekilde tanımlanır.
$$ R_i = \frac{y_i - \hat{y}(x_i)}{\alpha_i} $$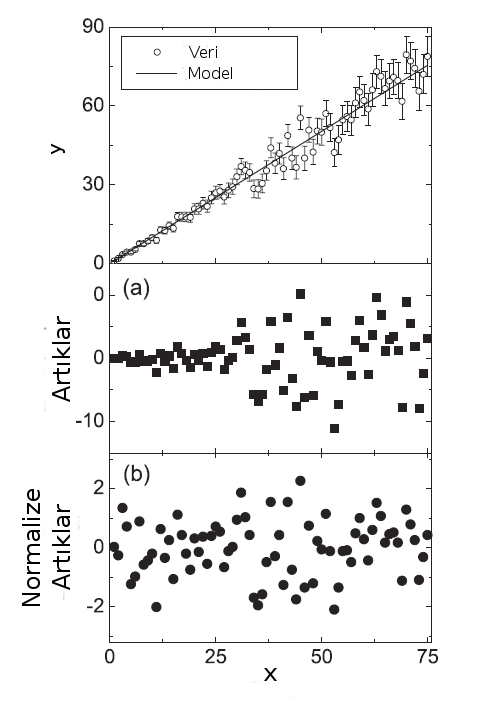
Bir Modelin Başarımına İlişkin Parametreler¶
Eğri Uyumlama dersinde de değindiğimiz gibi bir modelin başarımı veri noktaları ile o noktalara modelde karşılık gelen değerler arasındaki fark, daha doğru ifadeyle bu farkların karelerin toplamı, üzerinden tanımlanır. Bu fark ne kadar küçükse model o kadar başarılı adledilir. Ancak Artık Kareler Toplamı (ing. Residual Sum of Squares) olarak tanımlanan ve aşağıdaki şekilde ifade edilen bu toplam doğrudan bir model başarımı göstergesi değildir.
$$ S_r = \sum_{i=1}^{n} (y_{i} - \hat{y_i})^2 $$Kök Ortalama Kare Hatası/Sapması (ing. Root Mean Square Error/Deviation) ya da daha iyi bilinen adıyla "RMS Hatası" artıkların uyumlama etrafında ne kadar saçıldığını gösteren bir parametredir ve yine bir model başarımı göstergesi değildir.
$$ RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n} (y_{i} - \hat{y_i})^2} = \sqrt{\frac{S_r}{n}} $$RMSE yerine, ona çok benzer şekilde ancak fark kareler toplamının $n$ nokta üzerinden ortalaması yerine varyansa (ya da ölçüm hatalarının karesine) bölünmesiyle tanımlanan $\chi^2$ ve onun serbestlik derecesine normalize edilmesiyle tanımlanan indirgenmiş $\chi^2_{\nu}$ parametresi daha sık kullanılır. Bu parametre adıyla bilinen $\chi^2$-dağılımını göstermesi nedeniyle artıkların analizinde önemli bir avantaj sunar.
$$ \chi^2 = \sum_{i=1}^{n} \frac{(y - y_i)^2}{e_i^2} $$$$ \chi^2_\nu = \frac{\chi^2}{\nu} $$Burada sistemin $\nu$ serbestlik derecesi (dof, ing. degree of freedom), veri noktası sayısı ile model paramatreleri sayısı arasındaki farktır ($\nu = n - m$).
Ayrıca korelasyon katsayısı (ing. correlation coefficient, $r^2$) da lineer ya da lineer dönüştürülebilir bir modelin başarımını ifade etmek için kullanılmaktadır. Hatırlatmak gerekirse; korelasyon katsayısı bir modelin ortalamaya oranla başarısını gösterebilir. Doğrusal bir modelden daha karmaşık modelleri ortalamayla karşılaştırmak iyi bir fikir olmayacağı için bu ölçütün de kullanım alanı bu tür modellerle sınırlıdır. Zira korelasyon katsayısı özünde, normal dağıldığı varsayılan iki parametre arasındaki lineer korelasyonun derecesini gösterir.
$\chi^2$ dağılımı ve özelliklerine geçmeden önce artıkların incelenmesi için kullanılan başka bir yöntem olan gecikme grafiklerinden (ing. lag plot) bahsetmekte fayda vardır.
Gecikme Grafikleri¶
Bir bağlı değişkenin değerlerinin sırasının değiştirilerek o değerlere karşılık çizdirilmesiyle elde edilen grafiklere gecikme grafikleri (ing. lag plot) adı verilir.
Verinin bir sıra kaydırılarak çizilen gecikme grafiğine birinci dereceden gecikme grafiği adı verilir. Genellikle birinci dereceden gecikme grafikleri aşağıdaki amaçlarla kullanılmaktadır.
- Model uygunluğu
- Seri korelasyon/otokorelasyon ile kırmızı (korele) gürültünün tespiti
- Verinin rastgeleliğinin testi
- Dönemli (mevsimsel) dalgalanmalar
- Aykırı değerlerin tespiti
Gecikme Grafikleriyle Model Uygunluğu Testi¶
Örneğin aşağıdaki gibi ilk bakışta farkedilemeyen bir sinüsoidal bir değişimin, y-ekseninin bir kaydırılarak (numpy.roll fonksiyonu bu amaçla kullanılabilir) eski haline göre ($y_{lag,1} - y$) çizdirilmesi sonucunda elde edilen elipsoidal grafik $y$'nin $x$'le tek dönemli sinüsoidal yapıda değiştiğine ilişkin kuvvetli bir fikir vermektedir.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
np.random.seed(124)
x = np.linspace(0,48*np.pi,1000)
y = np.sin(x) + 0.1*np.random.rand(x.size)
plt.plot(x,y,'r+')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
# Gecikme grafigi
ylag1 = np.roll(y,1)
plt.plot(y, ylag1, 'r+')
plt.xlabel("y")
plt.ylabel("$y_{lag,1}$")
plt.show()
Diğer taraftan aralarında bir ilişki bulunmayan parametrelerin gecikme grafikleri de rastgele (ing. random) yapıdadır.
from matplotlib import pyplot as plt
import numpy as np
%matplotlib inline
np.random.seed(758)
x = np.linspace(0,10,100)
y = np.random.rand(100)*10
ylag1 = np.roll(y,1)
plt.plot(x,y,'ro')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
plt.plot(y,ylag1,'bo')
plt.xlabel("y")
plt.ylabel("$y_{lag,1}$")
plt.show()
Verinin Rastgeleliğinin Testi¶
Rastgelelik gösterip göstermediği bir gecikme grafiğiyle araştırılmak istenen bir değişenin otokorelasyon göstermesi durumunda gecikme grafiği lineer yapıdadır. Bu durum birkaç sebepten kaynaklanabilir. Örneğin zamana bağlı bir sinyaldeki gürültü, bir veri noktasının bir öncekinden bağımsız olmasını engelleyen (korele) bir gürültü olabilir (ing. red noise). Ya da zamanla fiyat artışı, enflasyon gibi bir önceki veri noktasının değerine bağlı veri noktaları içeren değişkenler otokorelasyon gösterirler ve bu durum gecikme grafikleriyle ortaya konabilir.
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
np.random.seed(43)
x = np.linspace(0,10,100)
veri = 2*x + 5 + np.random.randn(100)
plt.plot(x,veri,'ro')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
veri_lag1 = np.roll(veri,1)
plt.plot(veri[1:],veri_lag1[1:],'bo')
plt.xlabel("y")
plt.ylabel("$y_{lag,1}$")
plt.show()
veri_lag2 = np.roll(veri,2)
plt.plot(veri[2:],veri_lag2[2:],'bo')
plt.xlabel("y")
plt.ylabel("$y_{lag,2}$")
plt.show()
Dönemli Değişimlerin Gecikme Grafikleri¶
Mevsimsel nitelik gösteren değişenler (sıcaklık, nem, güneş lekesi sayısı vs.) için oluşturulan gecikme grafiklerinde bu türden çevrimli yapılar lineer yapılar olarak kendini gösterir.
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
np.random.seed(43)
x = np.linspace(0,16*np.pi,200)
gurultu = np.random.randn(200)
donemli_veri = 2*np.cos(3*x) + 2*np.sin(2*x+np.pi/4) + gurultu
plt.plot(x,donemli_veri,'ro')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
donemli_veri_lag1 = np.roll(donemli_veri,1)
plt.plot(donemli_veri[1:],donemli_veri_lag1[1:],'bo')
plt.xlabel("y")
plt.ylabel("$y_{lag,1}$")
plt.show()
Görüldüğü gibi dönemlilik içeren bu verinin birinci dereceden gecikme grafiği doğrusala yakın bir görüntüdedir. Ancak doğrusal değişimin başında varyansın artıp, ortasında maksimuma ulaşması, ardından da gecikme grafiğindeki değişimin sonuna doğru varyansın tekrar azalması, daha önce tek çevrimli bir sinüsün gecikme grafiğinde gördüğümüz elips yapısına da benzerlik göstermektedir. Sonuç olarak bu türden bir gecikme grafiği veride dönemlilik olabileceğini düşündürtür ve model aranırken dönemlilik içeren sinüs fonksiyonlarının lineer bileşimlerinin uyumlanması denenebilir.
Gecikme Grafiklerinde Aykırı Değer Yakalama¶
Bir değişkenin değerindeki aykırılıklar kendisini gecikme grafiklerinde de gösterir. Bu nedenle gecikme grafikleri aykırı değer yakalamak için de kullanılabilirler.
Örneğin son oluşturduğumuz dönemli değişim içeren donemli_veri veri dizimize birkaç aykırı nokta ekleyelim ve bunların gecikme grafiğinde ne şekilde davranacaklarına bakalım.
donemli_veri[::50] = [8, -6, 10, -7]
plt.plot(x,donemli_veri,'ro')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
donemli_veri_lag1 = np.roll(donemli_veri,1)
plt.plot(donemli_veri[:],donemli_veri_lag1[:],'bo')
plt.xlabel("y")
plt.ylabel("$y_{lag,1}$")
plt.show()
$\chi^2$ Dağılımı ve $\chi^2$ Testi¶
Bir x değişkenin ölçüm değerleri $x_i$ ve üzerindeki belirsizlikler $\sigma_i$ olmak üzere ağırlıklı ortalama
$$ \bar{x} = \frac{\sum_{j = 1}^{n} (x_j / \sigma_j^2)}{\sum_{j = 1}^{n} (1 / \sigma_j^2)} $$ile verilir.
Tüm ölçümler üzerinde aynı belirsizlik bulunuyorsa ($\sigma = \sigma_i$) bu durumda ağırlıklandırmaya gerek olmadğından ortalama değer doğrudan elde edilir.
$$ \bar{x} = \frac{(1 / \sigma^2) \sum_{j = 1}^{n} x_j}{(1 / \sigma^2) \sum_{j = 1}^{n} 1} = \frac{1}{N} \sum_{j = 1}^{n} x_j $$Ortalamanın Standart Sapması (ya da Varyansı) her bir veri noktasının hatası ($\sigma_i$) ya da tüm verinin standart sapmasından ($\sigma$) farklıdır:
$$ \sigma_{\nu}^2 = \frac{1}{\sum_{j = 1}^{n} (1 / \sigma_j^2)} $$Tüm ölçümler üzerinde aynı belirsizlik bulunuyor ya da verinin tamamının standart sapması biliniyor ise ($\sigma = \sigma_i$):
$$ \sigma_{\nu}^2 = \frac{\sigma^2}{N} $$Ölçümün (ya da ölçüm aletinin) belirsizliği:
$$ \sigma^2 \sim s^2 = \frac {1}{N-1} \Sigma_{j = 1}^n (x_j - \bar{x})^2 $$Sınırlı sayıda ölçüm alabilmekten kaynaklanan istatistiksel dalgalanma (Poisson):
$$ \sigma^2 = \nu \sim \bar{x} $$olmak üzere;
$\chi^2$-testi: $x_j$ olası değerleri için gözlenen bir frekans dağılımının $h(x_j)$, varsayılan bir olasılık dağılımına göre belirlenmiş olasılıklarını veren $N P(x_j)$ dağılımı ile karşılaştırılmasına dayanan testtir. Bu karşılaştırma için kullanılan $\chi^2$-istatistiği:
$$ \chi^2 = \sum_{j=1}^{n} \frac{[h(x_j) - N~P(x_j)]^2}{\sigma_j(h)^2} $$$\chi^2$ istatistiğinin gösterdiği dağılım $\chi^2$-dağılımı olarak adlandırılır. Bu dağılım $\Gamma$ (Gamma) dağılımının özel bir halidir. Hipotez testi, güven aralığı oluşturma (ing. confidence interval), uyum başarısı (ing. goodness of fit) gibi bir çok istatistiksel çıkarımda kullanılmaktadır. Nadiren Helmert dağılımı olarak da isimlendirilir.
Serbestlik derecesi ($\nu$): Veri sayısı (N) ile verilerden birbirlerinden bağımsız olarak belirlenen parametres sayısı (m) arasındaki farktır (N – m).
İndirgenmiş $\chi^2_{\nu} = \chi^2 / \nu$: $1$’e yakınsa $h(x_j)$ dağılımı $N~P(x_j)$ dağılımı ile uyumludur. Serbestlik derecesine karşılık verilen indirgenmiş $\chi^2_{\nu}$ tablolarından rastgele seçilen bir veri setinin, ana dağılımdan türetilmiş olup olmadğının olasılığı bulunur.
Testin Uygulanışı¶
$\chi^2$-testi genellikle gözlemsel verinin, gözlenen olaya ilişkin teori ile tutarlılığının sınanması için kullanılır. Genellikle testte sıfır hipotezi ($H_0$) “teorik yaklaşım gözlem verisi ile tutarlıdır.” şeklinde seçilir.
Sıfır hipotezi ($H_0$) doğru ise uyumlama sonrası artıkları, rastgele hatalardan kaynaklanır ve bu nedenle normal dağılım gösterir. Bu durumda her bir gözlem verisinin uyumlanan eğriden (ya da modelden) farklarının toplamı bir ki-kare dağılımı vereceğinden ki-kare testi uygulanabilir.
Test adımları şu şekilde uygulanır:
$\chi^2$-değeri (Pearson test istatistiği, $\chi^2$) aşağıda verilen en genel ifadeden (ya da daha önce verilen formüller kullanılarak) hesaplanır. Burada $O_i$: gözlenen değeri, $C_i$ modelden hesaplanan değeri, $\sigma_i$ gözlemsel verinin hatasını (ölçüm hatası ya da standart sapmasını) göstermektedir: $ \chi^2 = \sum \frac{(O_i - C_i)^2}{\sigma_i^2} $
Serbestlik derecesi ($\nu = N - m$) hesaplanır. Burada $N$ ölçüm sayısını, $m$ modelin parametre sayısını göstermektedir.
Sıfır hipotezi ($H_0$) kurgulanır. Sıfır hipotezi, model uyumlamalarında seçilen modelin veriyi uyumladığını ifade ederken, alternatif hipotez ise bunun tersini ifade eder. $\chi^2$ testinde test edilen $H_0$ sıfır hipotezidir.
Bir güven düzeyi seçilir.
Ki-kare ($\chi^2$) tablolarından ilgili serbestlik derecesi ve güven düzeyine karşılık gelen kritik $\chi^2$ değeri, hesaplanan $\chi^2$ ile karşılaştırılır.
Hesaplanan $\chi^2$ değeri, tablodaki kritik değerden küçük ise sıfır hipotezi (gözlem verisinin teori ya da model ile tutarlı olduğu) reddedilemez. Eğer büyük ise sıfır hipotezi reddedilir (teori ya da model gözlem ile tutarlı değildir görüşü için bir kanıt elde edilir).
$\chi^2$ testini verilen güven düzeyleri için kritik $\chi^2$ değerlerini tablolardan okuyup hesaplanan $\chi^2$ değeri ile karşılaştırarak yapmak yerine elde edilen $\chi^2$ değeri için, $H_0$'ın doğru olması durumunda o değerden daha büyük bir $\chi^2$ elde etme olasılığını veren p-değerini hesaplayıp ($p = P(\chi^2 > \chi^2_{hesap})| H_0$), bu değeri istatistiki anlamlılık seviyesi ile ($\alpha$ = 1 - güven düzeyi) karşılaştırmak mümkündür. Eğer hesaplanan bu p-değeri, istatistiksel anlamlılık seviyesinden ($\alpha$) büyükse $H_0$ reddedilemez. Aksi durumda $H_0$ reddedilir. Bu durum $H_1$ için bir kanıt teşkil eder.
$\chi^2$ değeri aynı parametre sayısına sahip iki modelin doğrudan karşılaştırılması için bir gösterge olarak da kullanılabilir.
Model uyumlamalarında serbestlik derecesi başına $\chi^2$ değeri ("indirgenmiş ki-kare", $\chi^2_\nu = \chi^2 / \nu$) kullanılıyorsa modelin başarımı $\chi^2_\nu$ değeri 1 ile karşılaştırılarak belirlenir.
$\chi^2_{\nu} = 1$ ise uyumlama gözlem verisinin üzerindeki hata mertebesinde iyi sonuç vermektedir. $\chi^2_{\nu} > 1$ ise uyumlama gözlem verisinin üzerindeki belirsizliği tam olarak modelleyememektedir. $\chi^2_{\nu} << 1$ ise uyumlama çok zayıftır. $\chi^2_{\nu} < 1$ gözlem verisi üzerindeki hata büyüktür sonuçlarına varılır.
Örnek: $\chi^2$ Testi¶
Diyelim ki bir öğrenci bir topu yerden 2.00 metre yükseklikten 50 kez bırakıyor ve topun yere düşme süresini kaydediyor ve aşağıdaki şekilde verilen histogramı elde ediyor. Şekildeki her bir dikdörtgenin yüksekliği kısa kenarında verilen zaman aralığına düşen ölçüm sayısını göstermektedir. Kesiksiz eğri, ölçümlerin ortalaması $T_{ort} = 0.635~s$, standart sapması $s = 0.020~s$ için Gaussyen dağılımı, kesikli eğri ise örnek ölçümlerin alındığı $\mu = 0.639~s$, $\sigma = 0.020~s$) ortalama değer ve standart sapma için ana Gaussyen dağılımı göstermektedir.
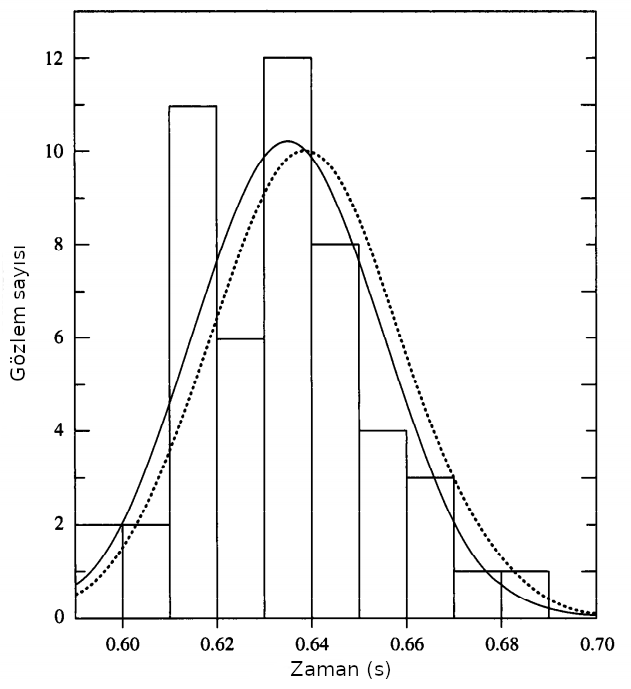
Söz konusu örnek için elde edilen değerler aşağıdaki gibi olsun. Verinin 1. sütıununda histogramı oluşturan her bir grubun ortasındaki zaman değeri, 2. sütunda o zaman aralığına denk gelen ölçüm sayısı, 3. sütunda $y_j = y(x_j) = N~P(x_j)$ her bir histogramın (1. sütunda verilen) $x_j$ değeri için ana dağılımın ortalama ve standart sapması kullanılarak hesaplanan olasılık fonksiyonu değerleri, 6. sütunda ise bu kez örnek dağılımın ortalama ve standart sapması kullanılarak hesaplanan olasılık fonksiyonu değerleri verilmektedir. 4 ve 7. sütunlarda verilen belirsizlikler o zaman aralığının ortasındaki zaman için hesaplanan olasılık fonksiyonu değerlerinin (3 ve 6. sütun) karekökleri (Poisson dağılım varsayımıyla) üzerinden hesaplanan sırasıyla ana dağılım ve örnek dağılım için belirsizliklerdir. Son olarak 5 ve 8. sütunlarda normalize artıklar verilmiştir.
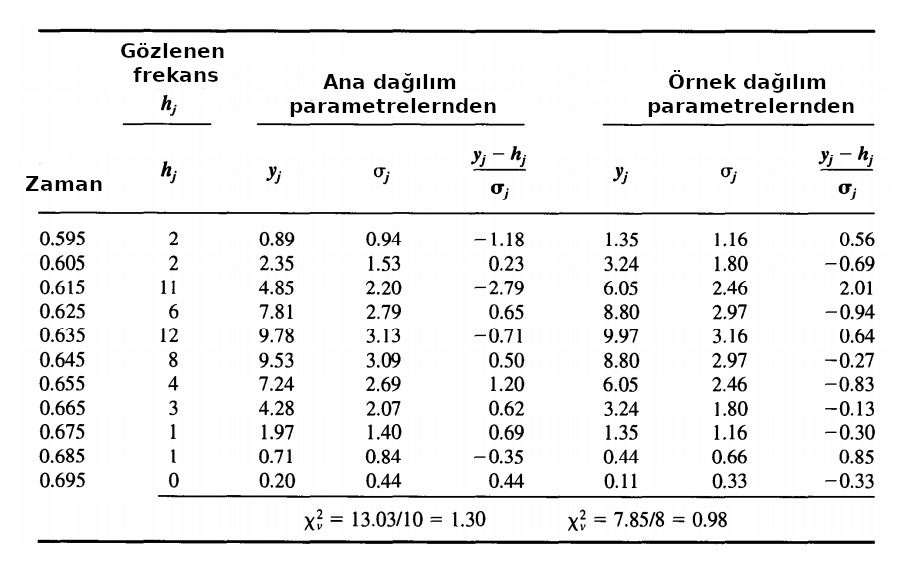
Sonuç olarak bu son sütunlardaki (5. ve 8.) değerlerin kareleri alınarak toplanmış $\chi^2$ değerleri ana dağılım için $13.03$, örnek dağılım için $7.85$ bulunmuştur. Ana dağılım için serbestlik derecesi, sadece toplam grup sayısı ($N$) üzerinden hesaplandığı için $\nu = 11 – 1 = 10$, örnek dağılım için ise grup sayısıyla birlikte ortalama ve standart sapma da bilindiği için $\nu = 11 – 3 = 8$’dir. Bu nedenle ana dağılım için indirgenmiş $\chi^2_{\nu} = 13.03 / 10 = 1.303$, örnek dağılım için ise $\chi^2_{\nu} = 7.85 / 8 = 0.98$ olarak bulunmuştur.
Aşağıda sadece bir bölümü verilen $\chi^2$-dağılımı olasılık tablosundan $\nu = 10$ serbestlik derecesi için $\chi^2_{\nu} = 1.3$ değeri $1.1784$ ile $1.344$ arasında kalıp bu değerlerin olasılıkları sırasıyla $0.30$ ve $0.20$’dir. Yapılacak basit bir lineer interplasyon $\chi^2_{\nu} \ge 1.3$ ‘ten daha büyük bir değer elde etme olasılığının $p \sim0.23$ (%23) olduğunu göstermektedir. Bir başka deyişle ana dağılımdan belilrlenen indirgenmiş $\chi^2_{\nu}$ değeri verinin saçılması ile %23 güvenilirlik seviyesinde uyumludur. Benzer bir analiz için $\nu = 8$ serbestlik derecesindeki örnek dağılım için yapıldığında $\chi^2_{\nu} \ge 0.98$ olma olasılığının %45 civarında olduğu bulunur.
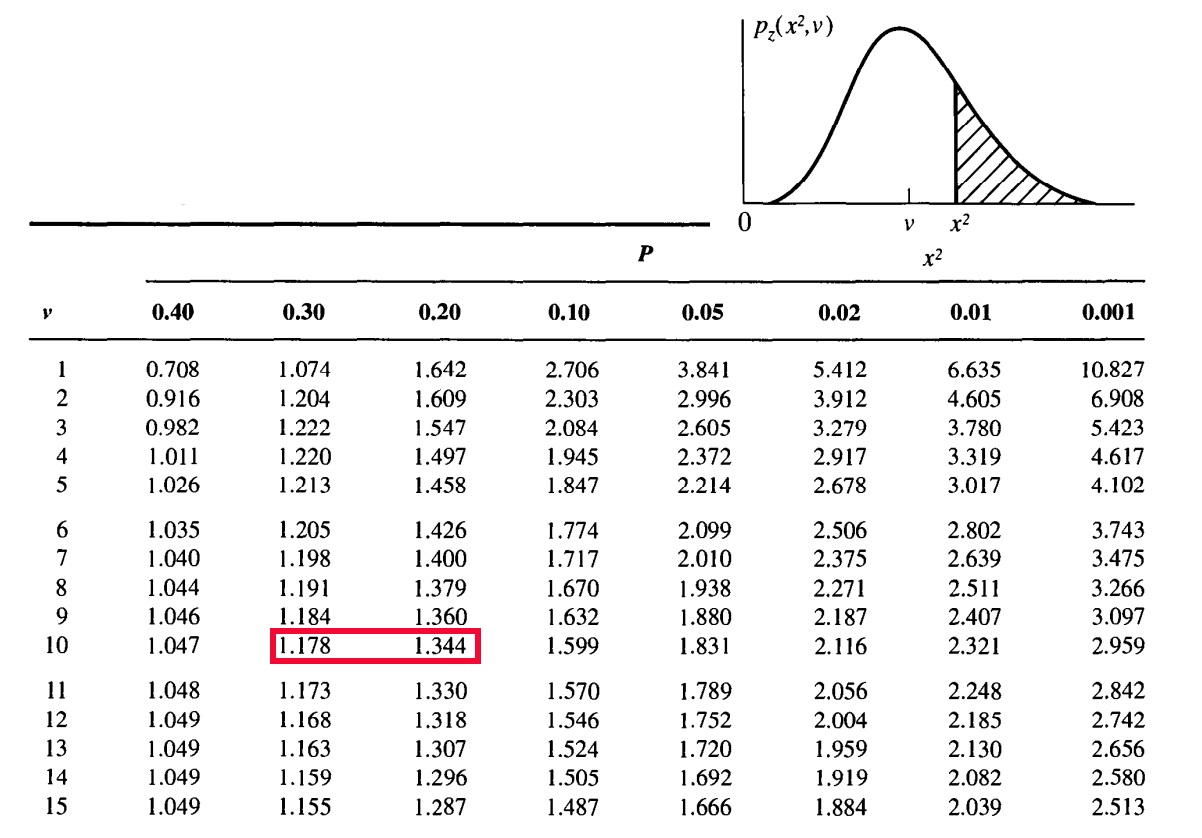
Örnekte çoğu zaman mümkün olmayan bir durum (ana dağılımın bilinmesi durumu), üzerinden tüm hesaplamalar yapılmıştır. Oysa ki çoğu zaman ana dağılım bilinmez. Bu durumda belirsizlikleri Gaussyen varsayarak belirlemek yerine, Poisson dağılımından hareketle $h(x_j)$ frekanslarının (örnekte 2. sütun) doğrudan karekökünü almak gerekir.
Örnekte olduğu gibi bazı gruplarda (binlerde) çok az sayıda ölçüm bulunması durumunda gruplar birleştirilerek daha büyük gruplar oluşturulabilir. Bu durumda yapılan istatistiksel testin de daha doğru sonuç vereceği değerlendirilmelidir.
$\chi^2$ Testinin İki Örnek Dağılımın Aynı Dağılımdan Türeyip Türemediğinin Kontrolü için Kullanılışı¶
$\chi^2$ testinin önemli uygulamalarından biri iki örnek veri setinin aynı ana dağılımdan alınıp alınmadığının belirlenmesinde kullanılmasıdır. $g(x_j)$ ve $h(x_j)$, $x$ değişkeninin iki ayrı örnekteki dağılımları olsunlar. Bu iki dağılımın $P(x_j)$ ana dağılımından alınıp alınmadığını belirlemek için $\chi^2$ testini her iki dağılıma ayrı ayrı uygulayıp hesaplanan $\chi^2$ değerlerinin $P(x_j)$ ile uyumlu olup olmadığı belirlenebileceği gibi ana dağılımdan bağımsız bir $\chi^2$ testi her iki dağılımın birden üzerine uygulanabilir. Bu durumda aşağıdaki ifadeden faydalanılır.
$$ \chi^2 = \sum_{j=1}^{n} \frac{[g(x_j) - h(x_j)]^2}{\sigma^2(g) + \sigma^2(h)} $$Her iki örnek dağılım, birbirlerinden tamamen bağımsız seçilirlerse serbestlik derecesi $\nu = n$ olur. Dağılımlardan biri diğerine normalize ise bu durumda $\nu = n - 1$ olmalıdır. İndirgenmiş $\chi^2$ , eğer 1’den çok büyük bir değere karşılık geliyorsa (bu değere karşılık gelen olasılık küçükse) bu iki dağıımın farklı ana dağılımlardan türetildiği sonucuna varılır.
Eğer $\chi^2$ için bulunan değere karşılık gelen olasılık büyükse bu durumda bu iki dağılımın farklı ana dağılımlardan türetildiği sonucu çıkarılamaz. Bu durumda gerçekten birbirine çok yakın iki ayrı dağılımdan türetilmiş ve eldeki verinin hassasiyeti dahilinde bu fark belirlenemiyor da olabilir.
Örnek: Doğru Uyumlama¶
$\chi^2$-testinin nasıl uygulandığını görmek için iyi ve basit bir uygulama doğrusal bir modeli gözlemsel veri üzerine uyumlamaktaır. Bu dersle birlikte verilen gözlemsel veriye bir doğru uyumlayalım ve Pearson $\chi^2$-testiyle uyumun başarısını (ing. goodness of fit) görelim.
Öncelikle veri setimizi inceleyelim.
from astropy.io import ascii
veri = ascii.read("veri/model_karsilastirma_chi2.dat")
veri
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
x = np.array(veri['col1'])
y = np.array(veri['col2'])
yhata = np.array(veri['col3'])
plt.errorbar(x,y,yerr=yhata,fmt=".",c="k")
plt.xlabel("x")
plt.ylabel("y")
plt.show()
Öncelikle Eğri Uyumlama dersinde daha önce gördüğümüz herhangi bir yöntemle bu veri setine bir doğru uyumlayalım. Öncelikle basit bir model için doğrusal en küçük kareler yöntemini seçerek basit bir Python fonksiyonuyla doğrusal uyumlama yapalım. numpy.polyfit() fonksiyonu deg=1 parametresiyle çalıştırıldığında bu amaca bizi ulaştıracaktır.
katsayilar = np.polyfit(x, y, deg = 1) # Sondaki 1 dogru uyumlamasini gosterir
m = katsayilar[0]
n = katsayilar[1]
print("Verilen veriye uyumlanan en iyi dogru: y = {:.4f}x + {:.4f}".format(m,n))
ymodel = m*x + n
plt.errorbar(x,y,yerr=yhata,fmt=".",c="k", label="veri")
plt.plot(x,ymodel,'r-', label="model")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="upper left")
plt.show()
Şimdi $\chi^2$ değerini kendi yazacağımız bir fonksiyonla hesaplayalım. Fonksiyonumuz $y$ ve $y_{hata}$ dizilerinin yanı sıra modelden hesaplanan $y_{model}$ değerlerini de gönderelim.
import numpy as np
kikare = lambda y,ye,ymod : ((y - ymod)**2 / ye**2).sum()
chi2 = kikare(y,yhata,ymodel)
dof = len(y) - len(katsayilar) # serbestlik derecesi
chi2_nu = chi2 / dof
print("Serbestlik derecesi: ", dof)
print("Chi^2 = {:.2f}, Indirgenmis Chi^2 = {:.2f}".format(chi2,chi2_nu))
Gayet basit bir fonksiyonla hem $\chi^2$, hem de $\chi^2_{\nu}$ istatistiklerini hesapladık. Şimdi bu istatistikleri kullanarak bir hipotez testi yapalım ve modelimizin başarısını bir hipotez testiyle test edelim.
- $H_0$: Lineer model gözlemsel veri ile tutarlıdır.
- $H_1$: Lineer model gözlemsel veri ile tutarlı değildir.
Bunun için öncelikle bir istatistiksel anlam seviyesi seçmeliyiz. $\chi^2$ testlerinde güven düzeyi yerine istatistiksel anlam ($\alpha$) tercih edilir. Ancak biz istatistiksel anlamın güven düzeyinin 1'den farkı olduğunu biliyoruz. Bu örnek için güven düzeyini %90 ($0.90$) olarak belirlemiş olalım. Bu güven düzeyine karşılık gelen istatistiksel anlam seviyesi ($\alpha$) ve $\chi^2$ değerini kullanarak $H_0$'ı test edelim. Bu amaçla $\chi^2$ dağılım tablolarını]kullanabilirsiniz. Böyle bir tablo kullanılırsa 0.10 istatistiksel anlam seviyesi için kritik $\chi^2$ değerinin $13.36$ olduğu ve hesaplanan $\chi^2 = 11.89 < 13.36$ olduğu görülebilir. Bu durumda lineer modelin gözlemsel veri ile %90 güven düzeyinde tutarlı olduğuna ilişkin $H_0$ hipotezinin reddedilmemesi gerekir. Sonuç olarak $H_0$ reddedilmez. Yani "lineer modelin gözlemsel veri ile tutarlı olması durumunda bu veri setini şans eseri elde etme olasılığı belirlenen istatistiksel anlamlılık seviyesinden büyüktür!". Aksi halde reddedilir ve bu da lineer modelin gözlemsel veriyle tutarlı olmadığını ifade eden $H_1$ için bir kanıt teşkil ederdi.
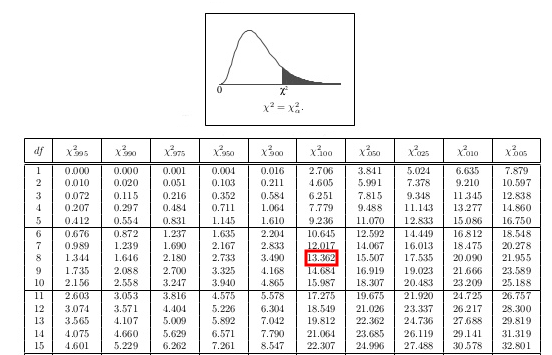
Python'da scipy.stats paketinin bu tür testler için geliştirilmiş fonksiyonlara sahip olduğunu daha önceki dağılımlar için yaptığımız uygulamalarda görmüştük. Yukarıda tablolarla yapılan test için scipy.stats.chi2.ppf fonksiyonunu da (ing. point percent function) kullanabiliriz. Ancak ppf fonksiyonuna verilen olasılık değerinin her zaman kritik değere kadarki ($\chi^2 < \chi^2_{kritik}$) olasılık olduğunu görmüştük. Dolayısı ile ppf() fonksiyonunun doğru kritik değeri verebilmesi için ona $\alpha$ istatistiksel anlamlılık seviyesi yerine güven düzeyi sağlanmalıdır ($1 - \alpha$).
from scipy import stats as st
alpha = 0.10
chi2_kritik = st.chi2.ppf(1-alpha, df=dof)
print("Kritik Chi^2 degeri: {:.4f}".format(chi2_kritik))
Belirlenen istatisiksel anlam seviyesi olan %10, lineer modelin veriyle uyumlu olması durumunda rastgele seçilecek 100 veri setinin 10 tanesinde uyumlanan doğrunun $13.3616$'dan büyük bir $chi^2$ değeri ($\chi^2 > 13.3616$) verirken 90'ında bundan daha küçük bir $\chi^2$ değeri elde edileceğini ortaya koymaktadır.
$\chi^2$ testini verilen güven düzeyleri için kritik $\chi^2$ değerlerini tablolardan okuyup (ya da scipy.stats.chi2.ppf ile bulup) hesaplanan $\chi^2$ değeri ile karşılaştırarak yapmak yerine elde edilen $\chi^2$ değeri için, o değerden daha büyük bir $\chi^2$ elde etme olasılığını veren p-değerini hesaplayıp, bu değer istatistiki anlamlılık seviyesi ile de karşılaştırılabilir. Hesaplanacak p-değeri, belirlenen lineer model doğruysa ($H_0$) bulunan $\chi^2$ değeri'nden büyük bir artık değerini rastlantısal olarak elde etme ihtimalini verir $p = P(\chi^2 \ge 11.89 | H_0$). Eğer bulunan p-değeri seçilen güven düzeyiyle belirlenen istatistiksel anlamlılıktan ($\alpha = 1 - 0.90 = 0.1$) küçük çıkarsa ($p < \alpha$) $H_0$ red edilir. Aksi halde $H_0$ red edilemez.
scipy.stats.chi2.cdf() fonksiyonu $\nu = 8$ için $\chi^2$'in 11.89'dan küçük olma olasılığını verecektir. Eğer bunun yerine $\chi^2$ ile karşılaştırmak isteniyorsa p-değerini elde etmek üzere ($P)\chi^2 > 11.89~|~H_0$) bu durumda scipy.stats.chi2.sf() fonksiyonu kullanılmalıdır.
olasilik = st.chi2.sf(chi2, df=dof)
print("{:d} serbestlik derecesi icin P(chi^2 > {:.2f}) = {:.4f}".\
format(dof, chi2, olasilik))
Sonuç olarak $\chi^2 > 11.89$ olma olasılığı %15.6 olarak bulunmuş oldu. $p = 0.1561$ olan bu değer $\alpha = 0.10$ ile karşılaştırıldığında $p > \alpha$ olduğu görülür. Bu durum $H_0$'ınb red edilmemesini gerektirir (tablo çözümüyle aynı sonuca ulaştık).
p-değeri ($p = 0.1561$) bize lineer model doğruysa ($H_0$) elde edilen $\chi^2 = 11.89$) değerinden daha büyük bir $\chi^2$ değeri verebilecek bir veri setini şans eseri türetme olasılığını verir.
Peki bu bulduğumuz olasılık değeri (p = %15.61) ne anlama gelmektedir?
Belirlenen parametreleriyle bu lineer modelin doğru olması durumunda modelden en az bu kadar artık verebilecek (modelden en az bu kadar uzakta) bir gözlemsel (deneysel) veri seti elde etme (ölçme) olasılığı %15.61'dir!
Bir başka deyişle, lineer modelin doğru olması durumunda bu modelden en fazla bu kadar artık verebilecek bir veri setini tamamen şans eseri üretme olasılığı %84.39'dur.
Diğer taraftan bulduğumuz bu p-değeri şu anlamlara gelmez:
- Lineer modelin doğru olma olasılığı %84.39'dur!
- Lineer modelin yanlış olma olasılığı %15.61'dir!
- Lineer modeli rededersek %15.61 ihtimalle yanılıyoruz demektir!
Zira $\chi^2$ testi aslında hiçbir modelin ne kadar olası olduğunu söylemez! Verilen güven düzeyinde ilgili modelle gözlenen artıklar kadar artık verebilecek bir veri setinin şans eseri elde edilme olasılığını söyler!
Örneğimizde lineer modelin çok başarılı olmadığı da ayrıca görülmektedir. Yukarıda kendi fonksiyonumuzu yazarak elde ettiğimiz bu istatistiki parametreleri LMFIT paketi fonksiyonlarıyla da elde edebiliriz. Bunun için öncelikle doğru modelinin parametrelerini tanımlamamız gerekir.
import lmfit as lm
dogru = lambda x,egim,kesme : egim*x + kesme
dogru_modeli = lm.Model(dogru)
print(dogru_modeli.param_names)
print(dogru_modeli.independent_vars)
Daha sonra uyumlama için makul birer başlangıç değeri vermemiz gerekir. Bu değerleri verinin basit bir grafiğinden kabaca belirleyebiliriz. Ayrıca weights parametresini kullanarak ölçüm hatalarına göre bir ağırlıklandırma da sağlayabiliriz.
sonuc = dogru_modeli.fit(y, x=x, egim=0.25, kesme=1.00, weights=1/yhata)
print(sonuc.fit_report())
Gördüğünüz gibi $\chi^2$ ve $\chi^2_{\nu}$ değerleri bizim basit $kikare$ fonksiyonumuzla hesapladıklarımızla aynıdır. $\chi^2 = 11.89$ değerini ve $dof = 10 - 2 = 8$ değerini scipy.stats.chi2 fonksiyonlarında kullanarak bir $\chi^2$ testi yapabileceğimiz gibi $\chi^2_{\nu} \sim 1.5$ değerinden hareketle uyumlamanın çok başarısız olmamakla birlikte gözlemsel verideki hatalar kaynaklı saçılmanın modelin başarımınını bir miktar etkilediği sonucuna varabiliriz.
Durbin Watson İstatistiği İle Model Başarımı Testi¶
Durbin-Watson istatistiği, bir regresyon analizinden artıklarda birinci dereceden gecikme grafiğinde otokorelasyonun varlığını tespit etmek için kullanılan bir test istatistiğidir. Durbin-Watson istatistiği aşağıdaki şekilde tanımlanır ve bu istatistik hesaplanıp, kullanılarak model uyumlamanın başarısı test edilebilir.
$$ \mathcal{D} = \frac{\sum_{i=2}^{N} [R_{i} - R_{i-1}]^2}{\sum_{i=1}^{N} [R_{i}]^2} $$Burada $\mathcal{D}$, Durbin-Watson istatistiği, $R_i$, uyumlamadan (fitten) artıklar, $R_{i-1}$ ise artıkların $i-1$'den başlayarak dizilmesiyle oluşan artıklardır. $\mathcal{D}$’nin alacağı değerlere göre aşağıdaki çıkarımlar yapılabilir:
- $\mathcal{D} = 0$: artıklar sistematik olarak korelasyon göstermektedir.
- $\mathcal{D} = 2$: artıklar normal dağılım göstermektedir.
- $\mathcal{D} = 4$: artıklar sistematik olarak antikorelasyona sahiptir.
Örnek olarak Durbin-Watson istatistiğinin yanı sıra pek çok başka model istatistiği de veren bir paket olan statsmodel paketi fonksiyonlarını modelleme için kullanalım. Durbin-Watson istatistiği yukarıdaki formülden kolayca hesaplanabilen bir istatistiktir. Dolayısıyla bu amaçla bir fonksiyon yazabilir ve modelleme işlemlerinizde scipy ya da numpy fonksiyonlarının yanı sıra bu yazdığınız fonksiyonu da kullanabilirsiniz. Ancak, burada hem bu fonksiyonu yazmayı size alıştırma olarak bırakmak hem de gelişmiş bir istatistiksel model paketini tanıtarak örneklemek açısından statsmodel ile bir modelleme örneği yapılacaktır.
Öncelikle yine modellemek istediğimiz verimizi oluşturalım ve grafiğini çizdirelim.
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
np.random.seed(48)
x = np.linspace(0,10,100)
y = -3*x + 5 + np.random.randn(100)*2
plt.plot(x,y,'ro')
plt.xlabel("x")
plt.ylabel("y")
plt.show()
Şimdi bu değişimi modellemek üzere statsmodel.api fonksiyonlarından en küçük kareler yöntemiyle model uyumlaması yapan OLS() (ing. Ordinary Least Squares) fonksiyonunu kullanalım. Öncelikle uyumlanacak doğrunun y-ekseninde bir kayma terimi (sabit) de içerdiğini belirtmek ve bu terimi de uyumlamak için statsmodel.api.add_constant fonksiyonu kullanılmaktadır. Bu terim bağımsız parametreye 1'lerden oluşan bir sabit terim ekler ve fit sırasında bu parametre de uyumlanır ($y = m*x + n*1$). Bu nedenle
X = sm.add_constant(x)
ifadesiyle bir $X$ iki boyutlu dizisi oluşturulmuştur. Bu ifade bağımsız değişken $x$'i $X = [x,1] \rightarrow y = m*x + n*1$ şeklinde ifade etmek ve uyumlama sırasında $m$ ve $n$ parametrelerinin bulunmasını sağlamaktadır.
OLS fonksiyonuna önce argüman olarak verinin bağımlı değişkenini içeren $y$ dizisi, sonra bağımsız değişken $x$ ve sabit parametreyi (1) içeren iki boyutlu $X$ değerleri numpy dizisi olarak sağlanmaktadır. Daha sonra uygulanan statsmodel.api.OLS() fonksiyonu bir model nesnesi döndürmekte bu model nesnesi aşağıdaki kod parçasında $model$ değişkenine atanmaktadır. Eğri uyumlamada gördüğünüz LMFIT fonksiyonunda olduğu gibi model nesnesinin uyumlama için kullanılan bir fit() fonksiyonu bulunmakta; model sonuçları ise bir sonuç nesnesi ile birlikte bu fonksiyonla döndürülmektedir. Bu nesnenin summary() metodu aralarında Durbin-Watson istatistiğinin de bulunduğu model istatistiklerini görüntülemek için kullanılmaktadır.
import statsmodels.api as sm
X = sm.add_constant(x)
model = sm.OLS(y, X)
sonuclar = model.fit()
print(sonuclar.summary())
İstendiği takdirde modele ilişkin istatistiklerin bazıları sonuç nesnesinin metodları ile ayrı ayrı da görüntülenbilir. Yapılması gereken yukarıdaki istenen istatistiği veren metodu sonuç nesnesi üzerine uygulamaktır. Örneğin model parametreleri params, bu parametrelerin hataları bse ve korelasyon katsayısı ($r^2$) rsquared metodları ile aşağıdaki şekilde görüntülenebilir.
print('Parametreler: ', sonuclar.params)
print('Standart hatalari: ', sonuclar.bse)
print('r^2: ', sonuclar.rsquared)
İstendiği takdirde uyumlanan fonksiyon yine bu nense üzerinden grafiğe aktarılabilir.
plt.plot(x,y,'ro', label='veri')
plt.plot(x,sonuclar.params[0]+sonuclar.params[1]*x, 'b-', label='model')
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
Oldukça gelişmiş model istatistikleri ve olanaklar sunan bu pakete daha ileri model örnekleri için tekrar döneceğiz. Ancak şu aşamada yaptığımız uyumlamanın Durbin-Watson İstatistiği'ne bakalım. $\mathcal{D} = 2.031~\sim~2$ bulunmuş olması artıkların normal dağılıma sahip olduğu iyi bir modele ulaşıldığını göstermektedir.
F Dağılımı ve F Testi¶
F-Testi, bir gözlem verisine yapılan iki farklı model uyumlamasının karşılaştırılıp hangisinin istatistiksel olarak daha başarılı bir uyumlama olduğunun belirlenmesi için kullanılan sınamalardan birisidir.
$F$ adı, varyans analizinin temellerini atan istatistikçi ve biyolog Ronald A. Fisher’a ithafen verilmiştir. Model seçimi için yapılan F-testinde takip edilmesi gereken temel adımları şöyledir:
Öncelikle bir sıfır hipotezi ($H_0$) belirlenir. $H_0$, genellikle aralarında karşılaştırma yapılan iki varyansın (modelden ya da ortalamadan fark kareler toplamının serbestlik derecesine bölümü) eşit olduğunu ifade eder ($F = s_{1} / s_{2} = 1$). Alternatif hipotez ($H_1$) ise bunun tam tersidir.
Karşılaştırılması istenen iki uyumlamanın artık kareler toplamı (ing. residual sum of squares, $S_r$) hesaplanır.
Rakip uyumlamalar için serbestlik dereceleri hesaplanır.
İstatistiksel anlamlılık derecesi $\alpha$ belirlenir.
$F$ değeri hesaplanır.
$F$ ile $\alpha$ karşılaştırılır ve $H_0$ bağlamında yorumlanır.
$F$-değeri aşağıdaki şekilde hesap edilir. Burada $S_{r_i}$, i. uyumlamadan (modelden) artık kareler toplamını; $m_i$, i. modelde kullanılan parametre sayısını, $n$ ise gözlemsel veri sayısını göstermektedir.
$$ F = \frac{(\frac{S_{r_1} - S_{r_2}}{m_2 - m_1})}{(\frac{S_{r_2}}{n - m_2})} $$Eğer modellerin parametre sayıları aynı ($m_1 = m_2$) ise F değeri aşağıdaki şekilde hesaplanabilir.
$$ F = \frac{S_{r_1}}{S_{r_2}} $$Artık kareler toplamlarının serbestlik derecelerine oranı bir $\chi^2$-dağılımı, $\chi^2$-dağılımlarının oranları ise bir F-dağılımı verir.
Böylece hesaplanan F değeri, bir F dağılımı üzerinde istatiksel anlamlılık derecesi ($\alpha$) ile ifade edilen kritik bir olasılık değeri ile karşılaştırılabilir bir değer olur.
F-testi için, karşılaştırılan artık ya da varyansların normal dağıldığı ve örneklemlerin birbirlerinden bağımsız olduğu varsayılır.
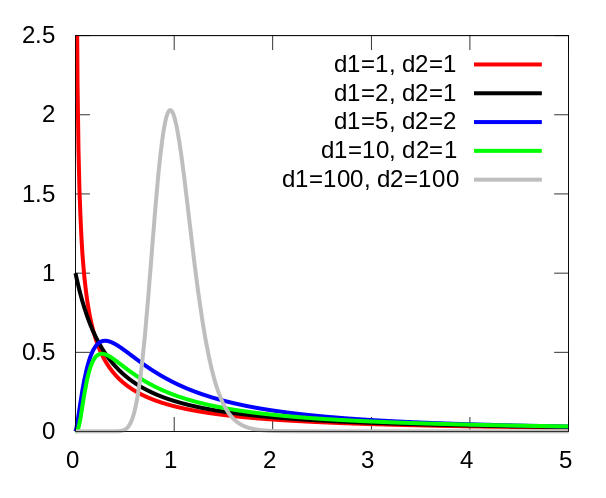
F dağılımı, bir olayın modellenmesinde kullanılan rakip modelin hangi güvenilirlik aralığı limitleri dahilinde birbirleri ile aynı başarımda olduğunun hesaplanmasında kullanılabilidiği gibi iki dağılımın karşılaştırılması temelindeki F-testinde, yani aynı ana dağılımdan seçilen iki örnek dağılımın standart sapmalarının belirli bir güven aralığı dahilinde karşılaştırılmasında da kullanılır. Bu testlerde kullanılan F-test istatistikleri F-dağılımına sahiptir. $U_i$ değerleri birer $\chi^2$-dağılımı ve $df_i$ değeleri bu dağılımların serbestlik dereceleri, $s_i^2$ değerleri bir modelden ya da ortalamadan fark kare toplam değerlerinin serbestlik derecesine bölümü, $\sigma_i^2$ ise ilgili normal süreçlerin standart sapmalarıd olmak üzere u test istatistikleri;
$$ X = \frac{U_1 / df_1}{U_2 / df_2} $$$$ X = \frac{s_1^2 / \sigma_1^2}{s_2^2 / \sigma_2^2} $$$$ s_1^2 = \frac{s_1^2}{df_1}, s_2^2 = \frac{s_2^2}{df_2} $$$$ F(x; df_1, df_2) = \frac{\sqrt{\frac{(df_1~x)^{df_2}~df_2^{df_2}}{(df_1~x + df_2)^{df_1 + df_2}}}}{x~B(\frac{df_1}{2},\frac{df_2}{2})} = \frac{1}{B(\frac{df_1}{2},\frac{df_2}{2})} (\frac{df_1}{df_2})^{\frac{df_1}{2}} x^{\frac{df_1}{2}-1}(1 + \frac{df_1}{df_2}~x)^{-\frac{df_1 + df_2}{2}}$$Örnek 1: F Testi¶
Varyansları $s_1 = 109.63$ ve $s_2 = 65.99$, örnek sayıları sırasıyla $n_1 = 41$ ve $n_2 = 21$ olan iki örneklem olsun. Bu iki varyansın $\alpha = 0.05$ güvenilirlik seviyesinde eşit olup olmadığını test etmek istiyor olalım.
- Sıfır hipotezi ($H_0$): Bu iki varyans arasında fark yoktur ($s_1 = s_2$).
- Alternatif hipotez ($H_1$) ise bu iki varyans eşit değildir ($s_1 \neq s_2$).
Çözüm : Bu örnek için F-istatistiği
$$ F = \frac{s_1}{s_2} = \frac{109.63}{65.99} = 1.66 $$şeklinde hesaplanır. Daha büyük olan varyansın bölünen, küçük olanın bölen olarak alındığına dikkat ediniz!
Yine bu örnek için serbestlik dereceleri $df_1 = n_1 – 1 = 40$, $df_2 = n_2 – 1 = 20$ ‘dir.
Bir sonraki adım F-tablolarından verilen güvenilirlik seviyesi $\alpha = 0.05$ iki taraflı bir test için ikiye bölünerek $\alpha / 2 = 0.025$ olanı seçilir. Zira burada bir varyansın diğerinden büyük (ya da küçük) olup olmaması değil, ikisinin eşit olup olmadığı test edilmektedir. Daha sonra $df_1 = 40$, $df_2 = 20$ serbestlik derecesi için verilen F-istatistiği değerine bakılır ($F = 2.287$). Biz bu değeri yine Python'da scipy.stats.f fonksiyonlarından ppf() fonksiyonunu kullanarak elde edebiliriz. Dikkat etmemiz gereken konu ppf() fonksiyonunun istatistiksel anlamlık ($\alpha$) yerine onun 1'den farkı olan güven düzeyini ($1 - \alpha$) argüman olarak aldığıdır. Fonksiyonun diğer parametreleri serbestlik dereceleridir ($df_1$ ve $df_2$).
from scipy import stats as st
alpha = 0.025
n1 = 41; n2 = 21
df1 = n1 - 1; df2 = n2 - 1
s1 = 109.63; s2= 65.99
F_hesap = s1 / s2
F_degeri = st.f.ppf(1-alpha, df1, df2)
print("Hesaplanan F-degeri = {:.3f}".format(F_hesap))
print("F-degeri = {:.3f}".format(F_degeri))
Bu değer hesaplanan $F = 1.66$ ile karşılaştırılır. Değer F-tablosunda $2.287$ olarak verilen değerden daha küçük ($F_{hesap} < F_{tablo}$) olduğundan $H_0$ hipotezi reddedilemez. Açık ki bu iki varyans eşit değildir. Ancak örneklem büyüklüklerine (ing. sample sizes) bakıldığında verilen güven düzeyinde bunların birbirinden farklı olarak değerlendiriilmesi için sebep yoktur.
Daha önceki hipotez testlerinde olduğu gibi model parametreleriyle bir F-değeri hesaplayıp, istatistiksel anlamlılık seviyesine ($\alpha$) karşılık gelen kritik F-değeriyle karşılaştırma yapılabileceği gibi; hesaplanan F-değerinin karşılık geldiği p-değerini (scipy.stats.sf (survival function)) bulup, doğrudan $\alpha$ ile karşılaştırmak da mümkündür.
p_degeri = st.f.sf(F_hesap,df1,df2)
p_degeri
Görüldüğü gibi bulunan p-değeri (0.11), seçilen istatistiksel anlamlılık seviyesinden ($\alpha = 0.025$) büyük olduğu için $H_0$ hipotezi reddedilemez. Yani rastgele süreçlerle, şans eseri, bu sonucu elde etmenin olasılığı seçilen istatistiksel anlamlılık seviyesinden büyüktür.
Örnek 2: Model Karşılaştırması İçin F Testi¶
Aşağıdaki tabloda birinci sütundaki zaman değerlerine karşılık ikinci sütunda bir niceliğin ölçüm değerleri görülmektedir.
| $t_i$ | $y_i$ |
|---|---|
| 2.5 | 10.07 |
| 2.8 | 11.07 |
| 5.4 | 14.59 |
| 6.5 | 20.75 |
| 9.2 | 27.94 |
| 9.5 | 31.50 |
| 11.0 | 38.04 |
| 13.3 | 49.90 |
| 14.6 | 60.72 |
| 16.4 | 75.57 |
Bu veri setini biri üstel ($y = A~e^{\alpha~t}$), diğeri kuvvet yasasına uyan $y = B~t^{\beta}$ iki ayrı modelle modelleyelim. Bu modellerden hangisinin veriyi daha iyi temsil edebildiğini doğrudan uyumlama eğrilerinden ya da artıklardan anlamamız her zaman mümkün olmaz. Uyumlamanın iyiliğini ölçebilecek istatistiksel yöntemlerin bazıları anlamlı bir seçim yapmaya yeterli olmayabilir. Örneğin en küçük kareler yöntemi ile bu veri setine yapılacak iki uyumlama için lineer korelasyon katsayılarını elde edelim.
Uyumlamak istediğimiz her iki fonksiyon da parametreleri bağlamında lineerleştirilebilir olduğu için lineer en küçük kareler yöntemlerini kullanabiliriz. Öncelikle fonksiyonları doğrusal hale getirelim.
$$ y_1 = A~e^{\alpha~t} \Rightarrow ln(y_1) = ln(A) + \alpha~t $$$$ y_2 = B~t^{\beta} \Rightarrow ln(y_2) = ln(B) + \beta~ln(t) $$Yukarıdaki fonksiyonları veriye uyumlamak için basit olması açısından numpy.polyfit() fonksiyonunu deg = 1 parametresiyle doğrusal bir model yapmak için kullanabiliriz. Ancak veri setimizi yukarıdaki lineerleştirmeye uygun olacak şekilde düzenlemeliyiz.
import numpy as np
t = np.array([2.5, 2.8, 5.4, 6.5, 9.2, 9.5, 11.0, 13.3, 14.6, 16.4])
y = np.array([10.07,11.07,14.59,20.70,27.94,31.50,38.04,49.90,60.72,75.57])
lnt = np.log(t)
lny = np.log(y)
ks_y1 = np.polyfit(t,lny,deg=1)
ks_y2 = np.polyfit(lnt,lny,deg=1)
# Katsayilari donusturmeliyiz
A = np.exp(ks_y1[1])
alpha = ks_y1[0]
B = np.exp(ks_y2[1])
beta = ks_y2[0]
# Fit fonksiyonlarini ekrana yazdiralim
print("y1 = {:.2f} e^({:.2f}t)".format(A,alpha))
print("y2 = {:.2f} t^{:.2f}".format(B,beta))
Fit fonksiyonlarını elde ettikten sonra bunları verimiz üzerine çizdirelim.
from matplotlib import pyplot as plt
%matplotlib inline
# Fit fonksiyonlarini biraz fazla nokta
# kullanarak cizdirelim
tyeni = np.linspace(t[0],t[-1])
y1 = A*np.exp(alpha*tyeni)
y2 = B*tyeni**(beta)
plt.plot(t,y,'ro',label="veri")
plt.plot(tyeni,y1,'b-',label="Ustel model")
plt.plot(tyeni,y2,'g-',label="Kuvvet yasasi")
plt.xlabel("t")
plt.ylabel("y")
plt.legend(loc="upper left")
plt.show()
Her ne kadar üstel model (mavi sürekli eğri) veriyi daha iyi temsil ediyor görünse de bir istatistik kullanmamızda fayda var. Örneğin $chi^2$ istatistiğini ve bu istatistiği hesaplamak üzere daha önce yazdığımız kikare fonksiyonunu, indirgenmiş $\chi^2_{\nu}$'yü döndürecek şekilde bir miktar düzenleyip bu amaçla kullanabiliriz. Yalnız fonksiyonu daha sonra yapacağımız F-testinde kullanmak üzere artıkları da döndürecek şekilde değiştirelim.
import numpy as np
kikare_nu = lambda y,ymod,dof : ((y - ymod)**2).sum()/dof
# Gozlemsel zaman degerleri icin modeller ne ongoruyor?
ymod1 = A*np.exp(alpha*t)
ymod2 = B*t**(beta)
kikarenu_ustel = kikare_nu(y,ymod1,(len(y)-2))
kikarenu_kuvvet = kikare_nu(y,ymod2,(len(y)-2))
print("Ustel model icin indirgenmis kikare degeri chi^2_red = {:.4f}".format(kikarenu_ustel))
print("Kuvvet modeli icin indirgenmis kikare degeri chi^2_red = {:.4f}".format(kikarenu_kuvvet))
Görüldüğü gibi üstel model gerçekten de $1$'e daha yakın bir indirgenmiş $\chi^2$ değeri vermiştir. Yine de bu modelleri karşılaştırmak için bir de F-testine başvuralım. Bu amaçla sıfır ve alternatif hipotezlerimizi probleme uyun şekilde oluşturalım.
- Sıfır hipotezi ($H_0$): "1. model (üstel), istatistiksel olarak 2. modele (kuvvet yasası) göre daha iyi bir uyumlamadır".
- Alternatif hipotez ($H_1$): "1. model 2. modele göre istatistiksel olarak daha iyi bir uyumlama değildir”
Bu örnek için F-istatistiğini 1. modelden artıkları bölen, 2. modelden artıkları bölünen olarak almak suretiyle hesaplayalım. Test ettiğimiz sıfır hipotezi ($H_0$) 1. model daha iyi bir uyumlamadır şeklinde ifade edildiğine göre ondan artıkların daha küçük olmasını bekleriz. Dolayısı ile artıkları büyük olan 2. modeli bölümün üstüne almamız gerekir.
Sr_ustel = sum((y-ymod1)**2)
Sr_kuvvet = sum((y-ymod2)**2)
F_hesap = Sr_ustel/ Sr_kuvvet
print("Hesaplanan F-degeri = {:.3f}".format(F_hesap))
Yine bu örnek için her iki model de ikişer parametre ($(A,\alpha)$, $(B,\beta)$) ve aynı sayıda ölçüm ($n = 10$) içerdiğinden serbestlik dereceleri $df_1 = df_2 = n – 2 = 8$'dir.
Bir sonraki adım F-tablolarından verilen istatistik anlam seviyesi için, önreğin $\alpha = 0.01$ tek taraflı bir test için olanının seçilerek (çünkü biz bu iki modelden artıklar arasında büyük bir fark olup olmamasını değil, seçilimiş bir modelin diğerinden daha iyi olup olmadığını sorguluyoruz) $df_1 = df_2 = 8$ serbestlik derecesi için verilen F-istatistiğine bakmaktır. Daha önce yaptığımız gibi bunun için scipy.stats.f.ppf() fonksiyonunu kullanacağız.
from scipy import stats as st
n = 10
df1 = df2 = n-2
alfa = 0.01
F_degeri = st.f.ppf(1-alfa, df1, df2)
print("Tablodan elde edilen F-degeri: {:.3f}".format(F_degeri))
Bu durumda $F_{hesap} = 0.089 < F_{tablo} = 6.029$ olduğundan $H_0$ hipotezi reddedilemez. %99 güven düzeyinde üstel modelin, kuvvet yasasıyla verilen modele üstün olduğu görülmektedir. Güven düzeyi %90’a ($\alpha = 0.10$) düşürülse dahi ($F = 2.5893$) $H_0$ reddedilemez.
Şimdi sıfır hipotezini ($H_0$): "2. model (kuvvet yasası), 1. modele (üstel) göre istatistiksel olarak daha iyi bir uyumlamadır", alternatif hipotezi ($H_1$) ise "2. model 1. modele göre istatistiksel olarak daha iyi bir uyumlama değildir" şekilnde değiştirelim ve sonuçta bir değişiklik olup olmayacağına bakalım.
Bunun için öncelikle F-istatistiğini fark kareler toplamının bölümde yerini değiştirerek hesaplayalım.
F_hesap = Sr_kuvvet / Sr_ustel
print("Hesaplanan F-degeri = {:.3f}".format(F_hesap))
Yine aynı şekilde her iki model de ikişer parametre ($(A,\alpha)$, $(B,\beta)$) ve aynı sayıda ölçüm ($n = 10$) içerdiğinden serbestlik dereceleri $df_1 = df_2 = n – 2 = 8$'dir. Bu serbestlik derecesi için verilen F-istatistiğini scipy.stats.f.ppf() fonksiyonunu kullanarak hesaplamıştık. $F_{hesap} = 11.212 > F_{tablo} = 6.029$ olduğundan $H_0$ bu kez reddedilir. Ancak bu kez reddedilen sıfır hipotezi kuvvet yasasının üstel modele göre veriye daha uygun olduğunu ifade etmektedir. Bu durum alternatif hipotez için, yani kuvvet yasasının üstel modele göre veriye daha uygun olmadığına yönelik görüşe kanıt teşkil eder. Her iki test de elimizdeki veriyi uyumlamada bize üstel modelin kuvvet yasasına üstün olduğu konusunda kanıt sağlamaktadır.
Varyans Analizi ANOVA¶
Varyans analizi (ing. Analysis of Variance, ANOVA) ikiden fazla örneklem söz konusu olduğunda bu örneklemlerlin ortalamaları arasında istatistiksel olarak anlamlı bir farkın olup olmadığını belirlemek için yapılır. Sadece iki grup söz konusu olduğunda genellikle t-testi kullanılır ve ANOVA ile aynı sonucu verir. Grupların ortalamları karşılaştırılırken eşit olup olmadıklarına karar vermek için doğal olarak varyanslarına ve grup büyüklüklerine bakılmalıdır.
Bir varyans analizi (ANOVA) yaparken aşağıdaki varsayımlar yapılır.
- Örnek gruplar normal dağılım göstermektedir.
- Gözlemlere ilişkin hatalar birbirlerinden bağımsızdır.
- Aykırı gözlemler bulunmamaktadır ya da ayıklanmıştır.
- Farklı örnek gruplarda, her bağımsız değişkene ilişkin varyans değerleri eşittir.
Varyans analizi de bir hipotez testine dayanır. ANOVA’nın sıfır hipotezi, tüm örnek grupların ortalama değerlerinin birbirlerine eşit olduğudur. Alternatif hipotez ise, "örnek grupların ortalama değerleri birbirlerine eşit değildir" şeklinde ifade edilir.
Test edilen olguya ilişkin ortalama değeri değiştirebilecek tek bir etkinin (faktörün) bulunması durumunda ana etken (ing. main effect) test edilmiş olur (ing. Factorial Analysis of Variance).
Deneysel araştırma alanlarında (örn. biyoloji, tıp, kimya) kullanılabildiği gibi, deneysel olmayan araştırma alanlarında (örn. astronomi) de kullanılabilmektedir ancak pek yaygın değildir. Deneysel araştırmalara örnek olarak; bir ilacın farklı dozajlarının sonuç etkide değişime sebep olup olmadığı testi bir varyans analizi ile yapılabilir. Böyle bir testte, tek bir değişken (dozaj) bulunduğundan bu teste tek yönlü ANOVA (ing. one way ANOVA) denir. Eğer bu deneyde farklı dozajların farklı cinsiyetlere etkileri ve cinsiyetler arası bir farklılığın olup olmadığı test edilmek istenirse iki değişken olması sebebiyle (dozaj ve cinsiyet) bu teste iki yönlü ANOVA (ing. two way ANOVA) denir.
Varyans analizinde diğer hipotez testlerine benzer olan aşağıdaki şematik yol takip edilir:
- Sıfır ve alternatif hipotezler belirlenir,
- Kritik olasılık değeri ($\alpha$) tanımlanır,
- Test istatistiği değeri belirlenir,
- Test istatistiiğinin istatistiksel olarak anlamlı olup olmadığı saptanır,
- Kritik değerler karşılaştırma sonucu $H_0$ bağlamında yorumlanır.
Örnek Varyans Analizi¶
4 farklı yıldız kümesi çalışıyor olalım. Sadece az sayıda yıldızının yaşını belrileyebildğimiz bu kümelerin aynı yaşta olup olmadığını anlamaya çalışyoruz. Kümelerin dönme noktasını sadece 5 yıldızdan belirleyemeyeceğimiz için yapabileceğimiz en iyi şey her bir kümedeki yıldızların yaşları ortalamasının belirli bir istatistik anlamlılık seviyesinde birbirleriyle eşit olup olmadığını sorgulamaktır. Birden fazla grubu birbirleriyle tek bir değişken (yaş) çerçevesinde karşılaştıracağımız için bu bir varyans analizi problemidir ve ANOVA tabloları adı verilen tablolarla çözümü kolaylaşırılabilir.
Öncelikle verimize bakalım.
| Küme 1 [Gyr] | Küme 2 [Gyr] | Küme 3 [Gyr] | Küme 4 [Gyr] |
|---|---|---|---|
| 6.8 | 2.4 | 3.2 | 2.9 |
| 5.5 | 4.3 | 5.4 | 2.8 |
| 6.2 | 3.5 | 4.1 | 1.7 |
| 7.6 | 5.1 | 2.0 | 1.9 |
| 3.1 | 1.0 | 3.0 | 3.2 |
Çözüm: Öncelikle sıfır ve alternatif hipotezleri tanımlayalım.
- $H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4$
- $H_1:$ Ortalamalar eşit değildir!
Öncelikle Python'ın sadece temel fonksiyonlarını hesaplamalar için kullanarak bir varyans analizi yaparak $H_O$ hipotezini test edelim. Bunun için öncelikle kümeleri birer numpy dizisi olarak tanımlayalım.
import numpy as np
kume1 = np.array([6.8,5.5,6.2,7.6,3.1])
kume2 = np.array([2.4,4.3,3.5,5.1,1.0])
kume3 = np.array([3.2,5.4,4.1,2.0,3.0])
kume4 = np.array([2.9,2.8,1.7,1.9,3.2])
Şimdi serbestlik derecelerini (grup sayıları $k = 4$, toplam örnek sayısı $N = 20$ olmak üzere) hesaplayalım.
k = 4
n = 5
N = n*k
df1 = k - 1
df2 = N - k
print("Birinci serbestlik derecesi: {:d}, ikinci serbestlik derecesi: {:d}".\
format(df1,df2))
Şimdi bir istatistiki anlam seviyesi tanımlayalım. %95 güven düzeyi ($\sim2\sigma$) için istatistiki anlamlılık seviyesi $\alpha = 0.05$ seçilmiş olsun. Her ne kadar $\alpha = 0.05$ için aşağıdaki gibi verilen F-tablosunu kullanabilirsek de biz scipy.stats.f alt modülü fonksiyonlarını kullanarak F-değerini hesaplayalım.

Bu değeri (tüm diğer istatistiklerin kritik değerleri gibi) ppf() (point percent function) fonksiyonuyla hesaplayabileceğimizi ve bu fonksiyona kritik değerin sol tarafındaki alanı verecek olan $\alpha$ yerine sağ tarafındaki alanı verecek olan $1 - \alpha$ değerini vermemiz gerektiğini biliyoruz.
from scipy import stats as s
alpha = 0.05
F_kritik = st.f.ppf(1-alpha, df1, df2)
print("alpha = {:.2f}, df1 = {:d}, df2 = {:d} icin F-kritik = {:.2f}".\
format(alpha,df1,df2,F_kritik))
Kritik değeri $F_kritik = 3.24$ bulduğumuza göre şimdi veriden F-değerini hesaplayıp bu değerle karşılaştırmalıyız. Bunun için bize grupların ortalamasıyla, bütün verinin ortalaması gerekir. Öncelikle her bir kümedeki yıldızların yaşlarının kümenin ortalamasından farklarının karelerini toplayarak SSE değerini aşağıdaki şekilde edelim.
$$ SSE_i = \sum_{j=1}^n (x_j - \bar{x_i})^2 $$$$ SSE = \sum_{i=1}^k \sum_{j=1}^n (x_j - \bar{x_i})^2 $$SSE_1 = np.sum((kume1 - kume1.mean())**2)
SSE_2 = np.sum((kume2 - kume2.mean())**2)
SSE_3 = np.sum((kume3 - kume3.mean())**2)
SSE_4 = np.sum((kume4 - kume4.mean())**2)
SSE = SSE_1 + SSE_2 + SSE_3 + SSE_4
print("SSE = {:.2f}".format(SSE))
Şimdi F-değerini hesaplamakta kullanacağımız ve grup ortalamlarının genel ortalamadan uzaklığını veren $SSB$ değerini aşağıdaki şekilde hesaplayalım.
$$ SSB = \sum_{i=1}^{k} n_i~(\bar{x_i} - \bar{x})^2 $$yildizlar = np.concatenate((kume1,kume2,kume3,kume4))
yildizlar_ort = yildizlar.mean()
SSB = len(kume1)*(yildizlar_ort - kume1.mean())**2 + len(kume2)*(yildizlar_ort - kume2.mean())**2 + \
len(kume3)*(yildizlar_ort - kume3.mean())**2 + len(kume4)*(yildizlar_ort - kume4.mean())**2
print("SSB = {:.2f}".format(SSB))
Görüldüğü gibi SSE aslında her bir yıldızın kendi grubunun ortalamasından sapmaları üzerinden hesaplanan grup içi varyansı, SSB ise her bir grubun ortalamasının genel ortalamadan farkına dayanan gruplar arası varyansı verdiği için aşağıdaki şekilde tanımlanan F-değeri, özünde grup-içi varyansın gruplar-arası varyansa oranıdır.
$$ s_1 = \frac{SSB}{df1} $$$$ s_2 = \frac{SSE}{df2} $$$$ F = \frac{s_1}{s_2} $$ANOVA analizlerinde genellikle aşağıdaki gibi bir tablo hazırlanır ve hesaplarda bu tablodan yararlanılır.
| Fark Kareler | Serbestlik Dereceleri | Ortalama Fark Kareler | F | |
|---|---|---|---|---|
| Kümeler Arası | SSB = 31.05 | $df_1$ = 4 - 1 = 3 | SSB / $df_1$ = 10.35 | 10.35 / 1.66 = 5.44 |
| Küme İçi | SSE = 30.44 | $df_2$ = 20 - 4 = 16 | SSE / $df_2$ = 1.66 | |
| Toplam | SSB + SSE = 61.49 | $df_1 + df_2$ = 19 |
s_1 = SSB / df1
s_2 = SSE / df2
F_hesaplanan = s_1 / s_2
print("Hesaplanan F-degeri = {:.2f}".format(F_hesaplanan))
Sonuç olarak elde edilen $F_{hesaplanan} = 5.44$, serbestlik derecelerine ve istatistiki anlam seviyesine karşılık tablolardan elde edilen $F_{kritik} = 3.24$ değeri ile karşılaştırıldığında ondan büyük olduğu görülür ($F_{hesaplanan} > F_{kritik}$). Bu nedenle sıfır hipotezi ($H_0$) reddedilir. Bu durumda incelenen kümelerdeki yıldızların ortalama yaşları arasında bir fark olduğu yönünde $\alpha = 0.05$ anlamlılık seviyesinde bir fark olduğuna dair istatistiki bir kanıt elde edilmiş olunur.
Seçilen istattistiki anlamlılık $\alpha = 0.001$ olsaydı,
from scipy import stats as s
alpha = 0.001
F_kritik = st.f.ppf(1-alpha, df1, df2)
print("alpha = {:.2f}, df1 = {:d}, df2 = {:d} icin F-kritik = {:.2f}".\
format(alpha,df1,df2,F_kritik))
$F_{kritik} = 9.01$ olur, bu durumda da $F_{hesaplanan} = 5.44 < F_{kritik}$ olacağından sıfır hipotezi ($H_0$) reddedilemezdi. Bir başka deyişle, bu düzeyde bu kümelerin yaşlarının farklı olduğu iddia edilemez, bu durum incelenen kümelerin yaşlarının eşit olduğuna bir kanıt teşkil ederdi.
Alternatif Çözüm: scipy.stats.f_oneway() fonksiyonu bir yönlü ANOVA analizi yapılmasına olanak sağlayan fonksiyonlara sahiptir. Çözümümüzü bu kez bu fonksiyonları kullanarak yapalım.
from scipy import stats as st
print(st.f_oneway(kume1, kume2, kume3, kume4))
Görüldüğü gibi f_oneway() sadece kritik F-değerini değil aynı zamanda daha önce de ne kadar kullanışılı olduğunu gördüğümüz Pearson p-değerini de vermektedir. Bu p-değerini kolaylıkla seçeceğiniz istatistiki anlamlılık seviyesiyle ($\alpha$) karşılaştırarak F-testi uyguylayabilirsiniz. Örneğin $\alpha = 0.01$ için $p < \alpha$ olacağı için kümelerin ortalamasının eşit olduğunu öne süre $H_0$ hipotezinin reddedilmesi gerekirken $\alpha = 0.001$ için $p > \alpha$ olduğundan $H_0$ reddedilemez. p-değeri yalnız başına da bir anlam taşır ve verdiği mesaj; bu kümelerin yaşlarının eşit olduğu hipotezinin en az $\sim0.009$’luk bir istatistik anlamlılık seviyesinde iddia edilebileceğidir. Bundan daha büyük istatistiki anlamlılık seviyelerinin tümünde $H_0$ reddedilir. Sonuç olarak bu kümelerin yaşlarının eşit kabul edilmesi ($H_0$) durumunda elimizdeki veri setinin örneklem hatasıyla şans eseri türemiş olma olasılığı %0.9'dur. Bu oran seçtiğimiz istatistik anlam seviyesinin $\alpha = 0.01$ olması durumunda $H_0$'ı reddetmememiz için yeterli değildir.
p-değerini scipy.stats.f.sf (ing. survival function) ile de hesaplayabilirdik.
from scipy import stats as st
p_degeri = st.f.sf(F_hesaplanan,df1,df2)
print("F = {:.2f} degerine karsilik gelen p-degeri = {:.6f}".\
format(F_hesaplanan, p_degeri))
Akaike Bilgi Kriteri¶
Akaike Bilgi Kriteri (ing. Akaika Information Criterion,AIC), bir modelin başarısını veren ölçütlerden biridir. Doğrudan bir modelin başarısını verebildiği gibi, farklı modellerin karşılaştırılabilmesinde de olanak sağlar. Bir sıfır hipotezinin testine dayanan bir değerlendirme yapılmadığı için bir modelin doğruluğunun hangi istatistiksel anlamlılık seviyesinde reddedilip edilmeyeceğiyle ilgili bir bilgi vermez. Dolayısıyla ilgilenilen modellerin tamamının veriye uyum sağlayıp sağlamamalarının bir göstergesi olmayıp, sadece bir karşılaştırmalarıdır.
Akaike Bilgi Kriteri (AIC) aşağıdaki şekilde tanımlanır ve $AIC$ değeri küçük olan modelin başarısı daha yüksektir.
$$ AIC = 2~k - 2~ln(\hat{L}) $$Burada $k$, modelde kullanılan parametrelerin sayısıdır. $\hat{L}$ ise modelin doğruluğu durumunda gözlem verisinin olabilirlik fonksiyonudur (ing. likelihood function).
Olabilirlik fonksiyonu, bir modelin önerdiği olasılık dağılımına göre tüm verilerin bu model ile oluşabilme olasılıklarının çarpımıdır. $AIC$ ya da bir çok hesapta olabilirlik fonksiyonunun kendisi kullanılabildiği gibi, kolay hesaplanabilirliği sebebiyle logaritması da kullanılmaktadır.
Görüldüğü gibi parametre sayısının artması durmunda $AIC$ değeri artar. Yani modelde kullanılan parametre sayısının fazlalığı, modelin gerçek değişimden çok gürültü modellemeye doğru eğilimde bulunacağı kabulu yapılır. Dolayısıyla daha az parametre sayısına sahip (daha basit) modellerin seçilmesi yönünde bir denge sağlamış olur.
Eğer uyumlama yapılmak istenen veri sayısı çok az ise $AIC$ daha fazla parametreye sahip olan modelin seçilmesine sebep olur. Bu sebep ile AIC düzeltmesi (AIC correction, $AICc$) tanımı yapılmıştır.
$$ AICc = AIC + \frac{2k~(k+1)}{n - k -1} $$Düzeltme terimindeki $n$, gözlem verisi sayısı; $k$ ise parametre sayısıdır.
$AIC$ ya da $AICc$ kullanımı için sınır koşul olarak $n/k > 40$ kullanılır. Yani gözlem verisi sayısı, modeldeki parametre sayısından en az 40 kat büyük ise $AIC$ kullanılabilir. Bu durumda parametre sayısı fazlalığının etkisi ihmal edilebilecek kadar küçük kalır. Eğer bu oran 40’tan daha küçük ise mutlaka $AICc$ kullanılmalıdır.
$AIC$ ya da $AICc$ değeri pozitif ya da negatif olabilir. Başarılı model her zaman daha küçük değere sahip olandır. $AIC$, farklı sayıda veriye sahip uyumlama işlemlerinde kullanılamaz. $AIC$, bir sıfır hipotezi sınaması olmadığı için sonuçta anlamlılık düzeyi, hipotez reddi gibi ifadeler kullanılmamalıdır.
Model uyumlamada AIC hesabı aşağıdaki şekilde yapılabilir.
$$ AIC = n~ln~(\frac{S_r}{n}) + 2k $$Daha önce de tanımlandığı gibi $S_r$ gözlemsel verinin modelden fark kareler toplamını ifade eder. $n$ gözlem verisi sayısı, $k$ modelin parametre sayısıdır.
Model seçimi durumunda:
- Modellerin tamamının $AIC$ değerleri yukarıdaki ifadeden hesaplanır.
- En düşük $AIC$ değerine ($AIC_{min}$) sahip olan model baz alınarak $AIC$ farkları ($Delta_i$) hesaplanır.
- Her bir modelin olabilirlik fonksiyonu değeri, o modelin $AIC$ değerinin minimum AIC değerine sahip modelden ($AIC_{min}$) farknın üstel bir ifadesi ile orantılıdır.
- Ardından modellerin Akaike ağırlıkları ($w_i$) hesaplanır. Bu değer, her bir model için bulunan olabilirlik fonksiyonunun karşılaştırma yapılan tüm modellerin toplam olabilirliklerine oranıdır.
olmak üzere,
$$ \mathcal{L}(g_i~|~y)~\alpha~e^{-\frac{1}{2} \Delta_i} $$$$ w_i = \frac{e^{-\frac{1}{2} \Delta_i}}{\sum_{r=1}^r e^{-\frac{1}{2} \Delta_r}} $$Örnek: Akaike Bilgi Kriteriyle Model Karşılaştırması¶
F-Testi ile model karşılaştırması için yaptığımız örneğe geri dönelim. Örneğimizin verisi aşağıdaki tabloda birinci sütunda verilen zaman değerlerine karşılık ikinci sütundaki bir niceliğin ölçüm değerlerinden oluşmaktaydı.
| $t_i$ | $y_i$ |
|---|---|
| 2.5 | 10.07 |
| 2.8 | 11.07 |
| 5.4 | 14.59 |
| 6.5 | 20.75 |
| 9.2 | 27.94 |
| 9.5 | 31.50 |
| 11.0 | 38.04 |
| 13.3 | 49.90 |
| 14.6 | 60.72 |
| 16.4 | 75.57 |
Bu veri setini biri üstel ($y = A~e^{\alpha~t}$), diğeri kuvvet yasasına uyan $y = B~t^{\beta}$ iki ayrı modelle modellemiş ve bu iki modeli F-testi ile karşılaştırmıştık. Bu kez bir de doğru modeli tanımlayalım ve bu modellerden hangisinin veriyi daha iyi temsil edebildiğini Akaike Bilgi Kriteri ($AIC$) kullanarak belirleyelim.
Uyumlamak istediğimiz her iki fonksiyon parametreleri bağlamında lineerleştirilebilirdi. Eklediğimiz son model de zaten lineer bir model olsun.
$$ y_1 = a_0 + a_1*t $$$$ y_2 = A~e^{\alpha~t} \Rightarrow ln(y_2) = ln(A) + \alpha~t $$$$ y_3 = B~t^{\beta} \Rightarrow ln(y_3) = ln(B) + \beta~ln(t) $$Yine numpy.polyfit() gibi basit bir fonksiyon kullanarak bu modelleri verimize uyumlayabiliriz ve bu modellerden verimizin fark kareleri toplamı, veri sayısı ve parametre sayısını dikkate alarak Akaike Bilgi Kriteri'ni ($AIC$), kritierin veri sayımız az olduğu için düzeltilmiş değerini ($AICc$) kendi yazabileceğiniz bir Python fonksiyonuyla hesaplayıp, model karşılaştırması yapabiliriz. Yine önce verimizi tanımlayalım ve uyumlamalarımızı yapıp veri üzerinde görerek başlayalım.
import numpy as np
t = np.array([2.5, 2.8, 5.4, 6.5, 9.2, 9.5, 11.0, 13.3, 14.6, 16.4])
y = np.array([10.07,11.07,14.59,20.70,27.94,31.50,38.04,49.90,60.72,75.57])
lnt = np.log(t)
lny = np.log(y)
ks_y1 = np.polyfit(t,y,deg=1)
ks_y2 = np.polyfit(t,lny,deg=1)
ks_y3 = np.polyfit(lnt,lny,deg=1)
# Katsayilari donusturmeliyiz
a0 = ks_y1[1]
a1 = ks_y1[0]
A = np.exp(ks_y2[1])
alpha = ks_y2[0]
B = np.exp(ks_y3[1])
beta = ks_y3[0]
# Fit fonksiyonlarini ekrana yazdiralim
print("y1 = {:.2f} + {:.2f}t)".format(a0,a1))
print("y2 = {:.2f} e^({:.2f}t)".format(A,alpha))
print("y3 = {:.2f} t^{:.2f}".format(B,beta))
Fit fonksiyonlarını elde ettikten sonra bunları verimiz üzerine çizdirelim.
from matplotlib import pyplot as plt
%matplotlib inline
# Fit fonksiyonlarini biraz fazla nokta
# kullanarak cizdirelim
tyeni = np.linspace(t[0],t[-1])
y1 = a0 + a1*tyeni
y2 = A*np.exp(alpha*tyeni)
y3 = B*tyeni**(beta)
plt.plot(t,y,'ro',label="veri")
plt.plot(tyeni,y1,'m-',label="Dogrusal model")
plt.plot(tyeni,y2,'b-',label="Ustel model")
plt.plot(tyeni,y3,'g-',label="Kuvvet yasasi")
plt.xlabel("t")
plt.ylabel("y")
plt.legend(loc="upper left")
plt.show()
Şimdi modellerimiz için $AIC$ ve $AICc$ değerlerini hesaplamak üzere basit bir fonksiyon yazalım ve verilerimiz ile modelimizi bu fonksiyona gönderereek $AIC$ ve $AICc$ değerlerini hesaplayalım
import numpy as np
def aic(y,ymodel,katsayilar):
Sr = np.sum((y - ymodel)**2)
n = len(y)
k = len(katsayilar)
AIC = n*np.log(Sr / n) + 2*k
AICc = AIC + (2*k*(k+1)) / (n - k - 1)
return(AIC,AICc,Sr)
AIC_1,AICc_1,Sr1 = aic(y,a0+a1*t,(a0,a1))
AIC_2,AICc_2,Sr2 = aic(y,A*np.exp(alpha*t),(A,alpha))
AIC_3,AICc_3,Sr3 = aic(y,B*t**beta,(B,beta))
print("Dogrusal model icin AIC={:.2f}, AICc = {:.2f}".\
format(AIC_1, AICc_1))
print("Ustel model icin AIC={:.2f}, AICc = {:.2f}".\
format(AIC_2, AICc_2))
print("Kuvvet yasasi modeli icin AIC={:.2f}, AICc = {:.2f}".\
format(AIC_3, AICc_3))
Her üç modelin parametre sayısı ve veri noktası sayısı da aynı olduğu için karşılaştırma doğrudan düzeltilmiş Akaika Bilgi Kriteri ($AICc$) üzerinden de yapılabilir. Böyle bir karşılaştırma üstel modelin diğer iki modele göre üstün olduğunu göstermektedir. Ancak öğretici olması açısından yukarıdaki şemaya bağlı kalarak bir tablo hazırlayyalım. Bunun için yukarıda tanımlanan $\Delta_i$ ve $w_i$ değerlerini de hesaplamamız gerekir. Bu hesaplar için gerekli bütün parametrelere sahibiz.
AICc = np.array([AICc_1,AICc_2,AICc_3])
AICc_min = np.min(AICc)
Delta = np.array([aicc-AICc_min for aicc in AICc])
expDelta = np.exp(-0.5*Delta)
wi = expDelta / np.sum(expDelta)
print("Sr_i: ", (Sr1,Sr2,Sr3))
print("Delta_i: ", Delta)
print("w_i: ", wi)
Bu değerleri bir tablo şeklinde ifade edelim
| Model | k | Sr | AICc | $\Delta_i$ | $w_i$ |
|---|---|---|---|---|---|
| Dogrusal | 2 | 242.68 | 37.61 | 20.33 | 0.000039 |
| Ustel | 2 | 31.79 | 17.28 | 0.00 | 0.999558 |
| Kuvvet | 2 | 356.44 | 41.45 | 24.17 | 0.000006 |
Bu değerlerden hareketle artık modelleri birbirleriyle karşılaştırmak mümkündür. Bunun için model ağırlıklarını birbirlerine bölerek, bir modelin diğerine göre "olabilirliğinin" ($\mathcal{L}$) ne kadar daha yüksek (olası) olduğunu belirlemeliyiz.
L2_1 = wi[1] / wi[0]
L2_3 = wi[1] / wi[2]
L1_3 = wi[0] / wi[2]
print("Ustel model dogrusal modele gore {:.2f} kat daha yuksek olabilirlige sahiptir".\
format(L2_1))
print("Ustel model kuvvet yasasi modeline gore {:.2f} kat daha yuksek olabilirlige sahiptir".\
format(L2_3))
print("Dogrusal model kuvvet yasasi modeline gore {:.2f} kat daha yuksek olabilirlige sahiptir".\
format(L1_3))
Sonuç olarak bu üç modelden üstel modelin eldeki gözlemsel veriyi modellemek konusunda başarımı en yüksek model olduğu tüm ölçütlerde görülmektedir. Aslında bu anlamda fark-karelere bakmak bile yaterli olabilirdi. Ancak buradaki üçüncü karşılaştırma anlamlıdır. Veriyi uyumlamak anlamında başarımı yakın iki modelden doğrusal modelin kuvvet yasası modeline göre 6.83 kat daha olası olduğu Akaike Bilgi Kritieri kullanılarak ortaya konmuş durumdadır. $AIC$ statsmodels ve LMFIT gibi gelişmiş model paketleri tarafından da verilen bir çıktı parametresidir. Yukarıdaki örneği bu modüllerden en az birini kullanarak çözmeyi deneyiniz. Bu modüllerin asıl avantajının parametreleri açısından örneğimizdeki gibi lineer modeller değil lineer-olmayan (nonlinear) söz konusu olduğunda ortaya çıktığını belirtmekte yarar vardır.
Bayesian Bilgi Kriteri¶
Bayesian Bilgi Kriteri (ing. Bayesian Information Criterion, BIC) de bir modelin başarısını veren bir başka bir ölçüttür. $AIC$ ile yakından ilişkilidir. Ancak ilave parametrelere daha hassastır ve temel olarak aşağıdaki şekilde tanımlanır.
$$ BIC = ln~(n)~k - 2~ln~(\mathcal{L}) $$Burada $n$, gözlem sayısı, $k$, modelde kullanılan parametrelerin sayısıdır. $L$ ise modelin doğruluğu durumunda gözlem verisinin olabilirlik fonksiyonudur (ing. likelihood function).
Tıpkı $AIC$ 'de olduğu gibi $BIC$ değerinin küçük olduğu modeller veriyi uyumlamada daha başarılıdır denilebilir. Eğri uyumlama işleminde kriter, aşağıdaki şekilde kullanılabilir. Burada $S_r$, yine modelden fark kareler toplamını ifade etmektedir.
$$ BIC = n~ln~(\frac{S_r}{n}) + k~ln~(n) $$Farklı modellerin $BIC$ değerleri arasındaki fark $\Delta_{BIC}$ aşağıdaki şekilde yorumlanabilir.
- $0 < \Delta_{BIC} < 2$, yüksek $BIC$ değerli modele karşı güçlü bir kanıt yoktur.
- $2 < \Delta_{BIC} < 6$, yüksek $BIC$ değerli modele karşı "pozitif" bir kanıt vardır.
- $6 < \Delta_{BIC} < 10$, yüksek $BIC$ değerli modele karşı "güçlü" bir kanıt vardır.
- $\Delta_{BIC} > 10$, yüksek $BIC$ değerli modele karşı "çok güçlü" bir kanıt vardır.
Kendiniz bir $BIC$ hesaplama fonksiyonu yazabileceğiniz gibi, statsmodels ve LMFIT gibi güçlü modülleri kullanarak $BIC$ değerlerini elde edebilir ve yukarıdaki şemayı kullanarak karşılaştırma da yapabilirsiniz.
Kaynaklar¶
- Measurements and their Uncertainties, Ifan G. Hughes & Thomas P.A. Hase, Oxford University Press, 2010
- Data Reduction and Error Analysis for the Physical Sciences, Philip R. Bevington & D. Keith Robinson, MC Graw Hill, 2003
- Gecikme Grafikleri - I
- Gecikme Grafikleri - II
- Durbin-Watson İstatistiği
- scipy.stats Modülü Dokümantasyonu
- numpy.random Modülü Dokümantasyonu
- statsmodels Dokümantasyonu
- 17 Statistical Hypothesis Tests in Python
- LMFIT Dokümantasyonu