Doç. Dr. Özgür Baştürk
Ankara Üniversitesi, Astronomi ve Uzay Bilimleri Bölümü
obasturk at ankara.edu.tr
http://ozgur.astrotux.org
Bu derste neler öğreneceksiniz?¶
Eğri Uyumlama¶
- Eğri Uyumlama
- Lineer Regresyon
- Lineer Olmayan İlişkilerin Lineerleştirilmesi
- Örnek: Lineer Olmayan İlişkilerin Lineerleştirilmesi
- Polinom Regresyonu
- Çok Değişkenli Lineer Regresyon
- En Küçük Kareler Minimizasyonu Yöntemi Genel İfade
- Doğrusal Olmayan En Küçük Kareler Yöntemi
- LMFIT Paketiyle Modelleme
- Eğri Uyumlamanın İnterpolasyon ve Ekstrapolasyon Amacıyla Kullanımı
- Kaynaklar
Eğri Uyumlama¶
Sadece astronomide değil, deneysel veriye bağlı herhangi bir bilim dalında gözlem veriye bir matematiksel modelin uyumlanması en sık başvurulan sayısal çözümleme tekniklerinden biridir. Uyumlanan matematiksel model, çoğu zaman analitik ifadesi bilinen bir eğridir. Bu eğriden yola çıkılarak i) verinin zaman içinde nasıl değiştiğini anlamak (trend analizi), ii) interpolasyon ve ekstrapolasyon yapmak; iii) herhangi bir model önerisinin başarısını ve öngörülen matematiksel modelin karşılık geldiği hipotezi sınamak olanaklı hale gelir.
Lineer Regresyon¶
Bir veriye yapılabilecek en basit model bir doğru uyumlamaktır. Eğri uyumlamada izlenen klasik istatistiksel (frekansçı; ing. frequentist) yaklaşımları anlamak için temel olarak lineer regresyonu ele alalım ve konuya en basit eğri (doğru) uyumlama yöntemiyle başlanılabilir. Lineer regresyonda eldeki veriye
$ y = a_0 + a_1 x $
modeli uyumlanmaya çalışılır. Model, deneysel veriyle ölçüm olayının kaçınılmaz bir şekilde hata barındırması nedeniyle birebir aynı olmayacağı için onun da üzerinde bir hata bulunacaktır. Lineer regresyonda amaç bu hatayı minimize etmektir. Hata $y_{deney}$ deneysel (ya da gözlemsel) ölçümleri, $y_{model}$ lineer modeli göstermek üzere, aşağıdaki şekilde ifade edilebilir.
$ e = y_{deney} - y_{model} = y_{deney} - (a_0 + a_1 x) $
Hatayı minimize etmek için çeşitli stratejiler düşünülebilir.
(a) Doğrudan bu farkın minimize edilmesi hedeflenebilir. Bu durumda her bir deney sonucu ile model arasındaki farklar alınır ve bu farkı minimum yapan model (doğru denklemi) aranır. $n$, nokta sayısını göstermek üzere;
$$ \sum_{i=1}^{n} e_i = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_i)) $$Bu durumda birden fazla farklı model aynı sonucu verebilir. Aşağıdaki grafikte gösterildiği gibi doğru model (sürekli doğru) ile açıkça yanlış olduğu görülen ikinci bir model (süreksiz doğru) modelden farklar toplandığında aynı $\Sigma e_i$ değerini verir. Birinci modelde gözlemsel veriler doğru üzerinde olduğu için modelden farkların her biri 0 olduğundan farklar toplamı da 0'dır. Aynı şey ikinci modelde her bir noktanın modelden farkı 0 olmasa da geçerlidir; zira ilk noktanın modelden farkı negatif olup, son nokta ile onun pozitif olması dışında büyüklüğü aynıdır. Ortadaki nokta da modelin üzerinde olduğu için modelden farklar toplamı yine 0'dır.
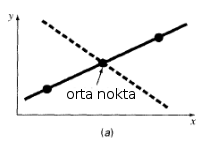
(b) Artıkların pozitif ya da negatif olabilmesi sebebiyle birbirlerini götürmelerinden kaçınmak için mutlak değer alınabilir. Bu stratejide minimize edilmesi istenen nicelik aşağıdaki şekilde ifade edilebilir.
$$ \sum_{i=1}^{n} |e_i| = \sum_{i=1}^{n} |y_{i} - (a_0 + a_1 x_i)| $$Bu durumda da birden fazla model aynı sonucu verebilir. Aşağıdaki dört gözlemsel nokta iki ayrı doğruyla $\Sigma |e_i| $ değerini verecek şekilde temsil edilebilir.
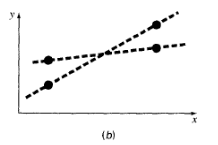
(c) Her iki problemden de kaçınmak için fark karelerin toplamının minimize edilmesi yoluna gidilir ki. Bu gayet iyi bilinen en küçük kareler minimizasyonu (ing. least squares minimization) tekniğidir. Bu teknikte aşağıda $S_r$ ile verilen niceliği minimize edecek model (burada doğru) aranır.
$$ S_r = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_i))^2 $$Bu klasik bir minimizasyon problemidir. Bir fonksiyonun uç değerleri (örneğin minimumu) birinci türevinin 0 olduğu noktada aranır. Ancak burada fonksiyonun türevinin alınacağı değişkenler $(x,y)$ değişkenleri değildir. Zira bu değerler değişmeyen, gözlemsel veriyi $(x_i,y_i)$ oluşturmaktadırlar. Değştirerek bu fonksiyonu minimize edecek değerlerin arandığı parametreler ise lineer modelin parametreleridir $(a_0,a_1)$. Dolayısıyla fonksiyonun türevinin alınacağı değişkenler de bu değişkenler olmalıdır. Daha sonra bu türevler 0'a eşitlenerek $a_0$ ve $a_1$'in bu farkları minimize edecek değerleri aranacak ve bu değerlerin işaret ettiği doğru "en iyi doğru modeli" olacaktır. Bu model tektir (ing. unique) ve bu stratejide ulaşılan en iyi modeldir.
$$ \frac{\partial S_r}{\partial a_0} = -2 \sum_{i=1}^{n} (y_{i} - a_0 - a_1 x_i) $$$$ \frac{\partial S_r}{\partial a_1} = -2 \sum_{i=1}^{n} [(y_{i} - a_0 - a_1 x_i) x_i] $$Bu türevler 0'a eşitlenip, toplam da bileşenlerine ayrılacak olursa;
$$ \sum_{i=1}^{n} y_{i} - \sum_{i=1}^{n} a_0- \sum_{i=1}^{n} x_i a_1 = 0 $$$$ \sum_{i=1}^{n} x_{i} y_{i} - \sum_{i=1}^{n} x_i a_0 - \sum_{i=1}^{n} x_i^2 a_1 = 0 $$İfadeler aşağıdaki şekilde düzenlenebliir. $n$ tane $a_0$ toplanınca $n~a_0$ elde edileceğine ve $a_0$ ile $a_1$'in toplam ifadelerinin dışına alınabileceğine dikkat ediniz.
$$ (n)~a_0 + (\sum_{i=1}^{n} x_i) a_1 = \sum_{i=1}^{n} y_{i} $$$$ (\sum_{i=1}^{n} x_i) a_0 + (\sum_{i=1}^{n} x_i^2) a_1 = \sum_{i=1}^{n} x_{i} y_{i}$$Bu basit iki bilinmeyenli ($a_0$ ve $a_1$) birinci dereceden iki denklem içeren bir denklem takımıdır, çözümü de tektir ve aşağıdaki şekilde ifade edilebilir (gösteriniz!).
$$ a_1 = \frac{n~\Sigma x_{i} y_{i} - \Sigma x_i \Sigma y_i}{n~\Sigma x_{i}^2 - (\Sigma x_{i})^2} $$$$ a_0 = \bar{y} - a_1~ \bar{x}, \bar{x} = \frac{\Sigma x_i}{n}, \bar{y} = \frac{\Sigma y_i}{n} $$Parametrelerin hataları;
$$ \epsilon_{a_1} = \sqrt{\frac{(n~\Sigma y_i^2 - (\Sigma y_i)^2 - a_1^2~(n \Sigma x_i^2 - (\Sigma x_i)^2))}{(n-2)(n~\Sigma x_i^2 - (\Sigma x_i)^2)}}$$$$ \epsilon_{a_0} = \sqrt{\epsilon_{a_1}^2 \frac{\Sigma x_i^2}{n}} $$Örnek: Lineer Regresyon¶
Bir roketin hızına karşılık maruz kaldığı hava direnci aşağıdaki çizelgede verilmiştir. Bu veriye en küçük kareler yöntemiyle en uygun doğru uyumlamasını yapınız.
| i | $x_i$ | $y_i$ |
|---|---|---|
| 0 | 10 | 25 |
| 1 | 20 | 70 |
| 2 | 30 | 380 |
| 3 | 40 | 550 |
| 4 | 50 | 610 |
| 5 | 60 | 1220 |
| 6 | 70 | 830 |
| 7 | 80 | 1450 |
Bu problemi öncelikle $a_0$ ve $a_1$ parametrelerini kendi fonksiyonlarımızla hesaplayacak şekilde çözelim.
import numpy as np
def dogru_denklemi(x,y):
"""
x ve y dizileri ile verilen veriye en iyi uyan dogrunun
y-eksenindeki kayma (a0) ve egim (a1) parametrelerini
donduren fonksiyon
"""
n = len(x)
a1 = (n*sum(x*y) - (sum(x)*sum(y))) / (n*sum(x**2) - (sum(x)**2))
a0 = (sum(y)/n) - a1*(sum(x)/n)
return(a0,a1)
x = np.arange(10,81,10.)
y = np.array([25.,70.,380.,550., 610.,1220.,830.,1450.])
n,m = dogru_denklemi(x,y)
print("Verilen veriye uyumlanan en iyi dogru: y = {:.4f}x + {:.4f}".format(m,n))
Şimdi veriyi ve en küçük kareler yöntemiyle veriye uyumladığımız en iyi doğru modelinin bir grafiğini çizdirelim.
%matplotlib inline
from matplotlib import pyplot as plt
# oncelikle x'in uc degerleri arasinda
# 50 noktadan olusan yeni bir x ekseni tanimlayalim
xyeni = np.linspace(x[0],x[-1])
# Bu ekseni dogru denkleminde yerine koyalim
yyeni = m*xyeni + n
plt.plot(x, y, 'o', xyeni, yyeni, '-')
plt.xlabel("x")
plt.ylabel("y")
plt.legend(['veri', 'model'], loc = 'best')
plt.plot
plt.show()
Şimdi aynı soruyu bu kez numpy.polfyit() fonksiyonu yardımıyla Python'a çözdürelim. numpy.polyfit istenen dereceden bir polinomu $x$ ve $y$ parametreleriyle sağlanan veriye uyumlayan bir fonksiyondur. 1. dereceden bir polinomun doğru olduğu bilgisinden hareketle $deg$ parametresini 1'e eşitleyerek aranan çözüme ulaşılabilir. Fonksiyon uyumlanan doğrunun (polinomun) katsayılarını ve istendiğinde parametre hatalarının türetilebileceği kovaryans matrisini verir.
%matplotlib inline
from matplotlib import pyplot as plt
import numpy as np
katsayilar = np.polyfit(x, y, deg = 1) # Sondaki 1 dogru uyumlamasıini gosterir
print(katsayilar)
print("uyumlanan dogrunun katsayilari: ", katsayilar)
# Istenirdse bu katsayilar tek tek kullanilarak dogrunun
# y degerleri hesaplabilecegi gibi,
# bu amaacla poly1d fonksiyonu da kullanilabilir.
dogru = np.poly1d(katsayilar)
ydogru = dogru(xyeni)
plt.plot(x, y, 'o', xyeni, ydogru, '-')
plt.xlabel("x")
plt.xlabel("y")
plt.legend(['veri', 'model'], loc = 'best')
plt.plot
plt.show()
Regresyon Katsayısı ve Tahmin Üzerindeki Standart Hata¶
Bu basit örnek sonrası uyumlanan doğrunun veri setini ne derecede temsil edebildiğine yönelik parametrelere geçelim. Regresyon katsayısı, bir doğrusal modelin eldeki veri setini aritmetik ortalamaya oranla ne ölçüde temsil edebildiğinin bir ölçüsüdür. Bu parametre aşağıdaki şekilde hesaplannır ve 1'e ne kadar yakınsa doğru modeli eldeki veri setine ortalamadan o denli daha iyi bir yaklaşımken, 0'a ne kadar yakınsa aritmetik ortalamaya göre temsil niteliği de o derece azdır.
$S_r$ verinnin modelden, $S_t$ aritmetik ortalamadan fark kareleri toplamını ifade etmek üzere aşağıdaki şekilde tanımlanır:
$$ S_r = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_i))^2 $$$$ S_t = \sum_{i=1}^{n} (y_{i} - \bar{y_i})^2, \bar{y_i} = \frac{\Sigma yi}{n} $$Korelasyon katsayısı $r$ ise,
$$ r^2 = \frac{|S_t - S_r|}{S_t} $$şeklinde tanımlandığı için açıkça modelin ortalamaya göre başarısını ifade etmektedir. Aşağıdaki grafiklerde aynı veri setinin aritmetik ortalamayla (solda) ve doğru modeliyle (sağda) hangi başarımda temsil edildiği model verinin modell etrafındaki dağılımıyla gösterilmiştir.
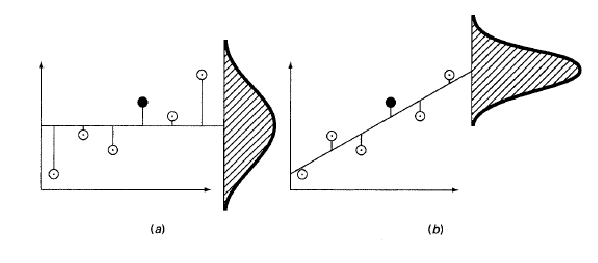
Nümerik bir örnek için tekrar roket hızına karşılık hava direnci örneğimize dönelim ve bu örnek için kendi yazdığımız dogru_uyumlama fonksiyonu korelasyon katsayısını da hazırlamak üzere biraz geliştirelim.
import numpy as np
def lineer_regresyon(x,y):
"""
x ve y dizileri ile verilen veriye en iyi uyan dogrunun
y-eksenindeki kayma (a0) ve egim (a1) parametrelerini
ve lineer korelasyon katsayisini hesaplayarak
donduren fonksiyon
"""
n = len(x)
a1 = (n*sum(x*y) - (sum(x)*sum(y))) / (n*sum(x**2) - (sum(x)**2))
a0 = (sum(y)/n) - a1*(sum(x)/n)
Sr = sum((y - a0 - a1*x)**2)
St = sum((y - y.mean())**2)
r2 = (np.abs(St - Sr) / St)
return(a0,a1,r2)
x = np.arange(10,81,10.)
y = np.array([25.,70.,380.,550., 610.,1220.,830.,1450.])
n,m,r2 = lineer_regresyon(x,y)
print("Verilen veriye uyumlanan en iyi dogru: y = {:.4f}x + {:.4f}".format(m,n))
print("Korelasyon katsayisi r = {:.2f}".format(np.sqrt(r2)))
Korelasyon katsayısı r'nin yerine genellikle karesi $r^2 = 0.94^2 = 0.88$ kullanılır. $r^2$, yukarıdaki örnekte lineer modelin, verinin üzerindeki belirsizliğin %88'ini açıklayabildiğini, ortalamaya oranla getirdiği iyileştirmenin bu düzeyde olduğunu göstermektedir.
Bu doğruya dayanarak yapılacak tahminlerin üzerindeki standart hata, tahmin üzerindeki standart hata parametresi ($S_e = S_{y/x}$) (ing. standard estimation error) ile verilir.
$$ S_e = S_{y/x} = \sqrt{\frac{S_r}{n - 2}} $$Sr = sum((y - n - m*x)**2)
Syx = np.sqrt(Sr / (len(y) - 2))
print("Tahmin üzerindeki standart hata: {:g}".format(Syx))
Ortalamanın standart sapması ($S_y$) ise
$$ S_{y} = \sqrt{\frac{S_t}{n - 1}} $$ile verilir. Standart sapma, sadece ortalama üzerinden hesaplandığı için serbestlik derecesi (ing. degrees of freedom) $n - 1$ iken, tahmin üzerindeki standart hata ise $a_0$ ve $a_1$ şeklinde iki parametre içeren bir model üzerinden hesaplandığı için serbestlik derecesi, $n - 2$'dir. Dolayısı ile tahmin üzerindeki standart hata aslında lineer modelin standart sapmasıdır. Bu durum verinin ortalama ve lineer model etrafında nasıl dağıldığına bakılarak görülebilir. Tıpkı aşağıdaki şekilde olduğu gibi örnekte de verinin lineer model etrafındaki dağılımının düzeyini ifade eden tahmin üzerindeki standart hatanın (sağdaki dağılımın standart sapmasının), ortalama etrafındaki dağılımını ifade eden standart sapmadan küçük olması ($S_{y/x} < S_y$) beklenir; zira korelasyon katsayısının ($r^2 = 0.88$) 1'e yakın olması bunu söylemektedir.

Ortalama etrafındaki dağılımın standart sapmasını hesaplanacak olursa:
Sy = np.sqrt(np.sum((y-y.mean())**2) / (len(y) - 1))
print("Standart sapma: {:g}".format(Sy))
Lineer modelin, veriyi temsil etmekteki ortalamaya göre başarısı buradan da görülebliir: $S_{y/x} = 189.79 < S_y = 508.26$.
Regresyon katsayısı aslında tek başına verinin lineer modelle ortalamay göre ne denli başarıyla temsil edildiğini vermektedir. Dolayısyla verinin kendi içindeki değişimin doğasından bağımsız olarak değerlendirilmemesi gerekir. Aşağıda verilen dört grafikte verilen dört farklı veri seti için $y = 3 + 0.5~x$ doğrusunun lineer korelasyon katsayıları ($r^2$) eşittir (Anscombe 1973). Bu grafikten hareketle lineer korelasyon katsayısına bakmadan önce verinin değişiminin doğasına bakılması gerektiği görülmektedir.
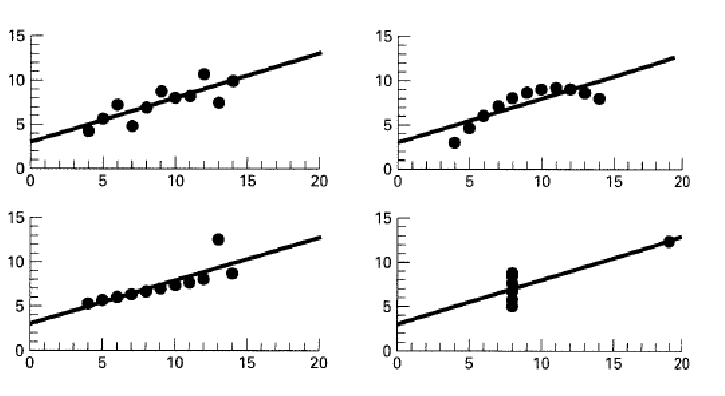
Lineer Olmayan İlişkilerin Lineerleştirilmesi¶
Bazı doğrusal olmayan ilişkilerin logaritmanın ve üs alma işleminin özelliklerini kullanarak doğrusal hale getirilmesi (lineerleştirilmesi) mümkündür. Bu özellikler, bu ilişkilerin analitik formlarının belirlenmesinde büyük kolaylık sağlar, zira lineer model basit bir modeldir ve uyumlama işlemi de görece kolaydır.
Üstel Fonksiyonların Lineerleştirilmesi¶
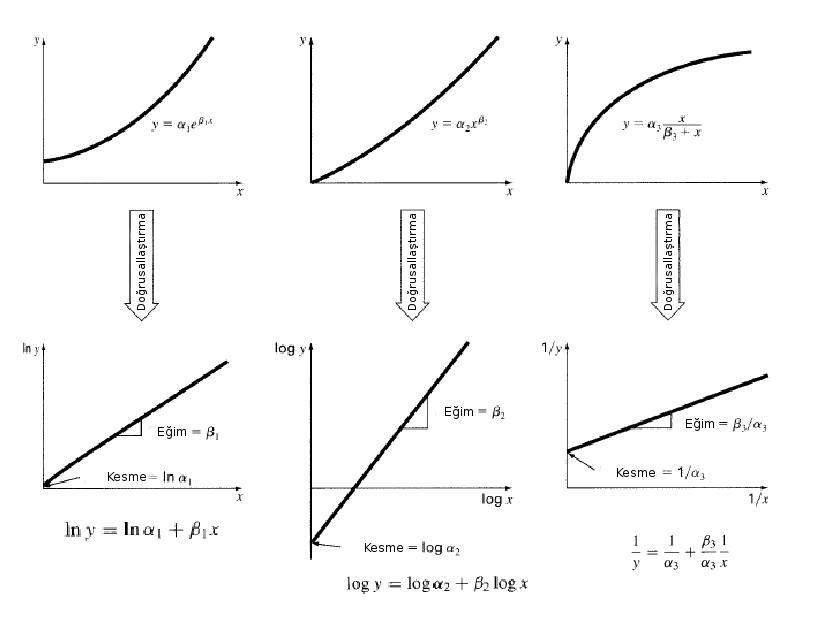
Üstel fonksiyonlar logaritma alınarak aşağıdaki şekilde doğrusallaştırılabilir.
$$ y = \alpha_1 e^{\beta_1 x} $$olmak üzere, her iki tarafın logaritması alınacak olursa;
$$ ln(y) = ln(\alpha_1) + \beta_1~x $$şeklinde ifade edilebilir. Bu durumda ilişkiyi lineerleştirmek için yapılması gereken tek şey her iki tarafın logaritmasını almak olduğundan; veri setindeki $x$ dizisi olduğu gibi bırakılırken $y$ ölçümlerinin logartiması alınır ve yukarıda anlatıldığı şekilde en küçük kareler yöntemiyle (ya da daha sofistike bir teknikle) lineer regresyon yapılarak doğrunun parametreleri ($a_0 = ln(\alpha_1)$ ve $a_1 = \beta_1$) hesaplanır. Bu parametreler hesaplandıktan sonra istenirse ilişki doğrusal form ya da ($ln(y) = ln(\alpha_1) + \beta_1~x$) üstel formda ($ y = \alpha_1 e^{\beta_1 x} $) ifade edilebilir.
Kuvvet Fonksiyonlarının Lineerleştirilmesi¶
Kuvvet fonksiyonları da logaritma alınarak aşağıdaki şekilde doğrusallaştırılabilir.
$$ y = \alpha_2 x^{\beta_2} $$olmak üzere, her iki tarafın logaritması alınacak olursa;
$$ log(y) = log(\alpha_2) + \beta_2~log(x) $$şeklinde ifade edilebilir. Bu durumda ilişkiyi lineerleştirmek için yapılması gereken tek şey her iki tarafın logaritmasını almak olduğundan; veri setindeki $x$ ve $y$ dizilerinin logartimaları alınır ve yukarıda anlatıldığı şekilde en küçük kareler yöntemiyle (ya da daha sofistike bir teknikle) lineer regresyon yapılarak doğrunun parametreleri ($a_0 = log(\alpha_2)$ ve $a_1 = \beta_2$) hesaplanır. Bu parametreler hesaplandıktan sonra istenirse ilişki doğrusal form ($log(y) = log(\alpha_2) + \beta_2~log(x)$) veya kuvvet yasası formunda ($ y = \alpha_2 x^{\beta_2} $) ifade edilebilir.
Rasyonel Bazı Fonksiyonların Lineerleştirilmesi¶
Aşağıdaki yapıda verilen rasyonel bir fonksiyon eşitliğin her iki tarafının 1'e bölünmesiyle doğrusallaştırılabilir.
$$ y = \alpha_3 \frac{x}{\beta_3 + x} $$olmak üzere, her iki taraf 1 ile bölünecek olursa;
$$ \frac{1}{y} = \frac{1}{\alpha_3} + \frac{\beta_3}{\alpha_3}~\frac{1}{x} $$şeklinde ifade edilebilir. Bu durumda ilişkiyi lineerleştirmek için yapılması gereken tek şey her iki tarafı 1 ile bölmek olduğundan; veri setindeki $x$ ve $y$ dizileri de 1 ile bölünür ($1/x$ ve $1/y$) ve yukarıda anlatıldığı şekilde en küçük kareler yöntemiyle (ya da daha sofistike bir teknikle) lineer regresyon yapılarak doğrunun parametreleri ($a_0 = 1 / \alpha_3$ ve $a_1 = \beta_3 / \alpha_3$) hesaplanır. Bu parametreler hesaplandıktan sonra istenirse ilişki istenen formda ifade edilebilir.
Aşağıda her üç durum da grafiklerle gösterilmiştir.
Örnek: Lineer Olmayan İlişkilerin Lineerleştirilmesi¶
Bir roketin hızına karşılık maruz kaldığı hava direnci örneği üzerinden devam ederek, bu örnekteki veriye daha iyi bir model bulunup bulunamayacağına bakalım. Hava direncinin roket hızının kuvvetiyle değiştiğini varsayarak, kuvvet yasasıyla bir ilişki aramayı deneyelim. Bu durumda,
$$ y = \alpha x^{\beta} $$olmak üzere, her iki tarafın logaritması alınacak olursa;
$$ log(y) = log(\alpha) + \beta log(x) $$doğrusal ilişkisi için veri ile en küçük fark kareleri verecek modelin $\alpha$ ve $\beta$ parametrelerini arayalım. Bun amaçla daha önce yazdığımız lineer_regresyon fonksiyonunu kullanabiiriz.
import numpy as np
x = np.arange(10,81,10.)
y = np.array([25.,70.,380.,550., 610.,1220.,830.,1450.])
logx = np.log(x)
logy = np.log(y)
n,m,r2 = lineer_regresyon(logx,logy)
print("Verilen veriye uyumlanan en iyi dogru: y = {:.4f}x + {:.4f}".format(m,n))
print("Korelasyon katsayisi r^2 = {:.2f}".format(r2))
Görüldüğü gibi bu modelin korelasyon katsayısı daha da yüksek ($r^2 = 0.95$) çıkmıştır. Bu durumda bu modeli diğer modele göre daha üstün kabul edebiliriz. Her iki modeli de verini üzerine çizdirelim.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
xyeni = np.linspace(x[0],x[-1])
ykuvvet = (np.exp(n))*(xyeni**m)
# veriye dogrudan dogru uyumlayarak karsilastirma yapalim
ydogru = lineer_regresyon(x,y)[0] + lineer_regresyon(x,y)[1]*xyeni
plt.plot(x, y, 'o', xyeni, ydogru, '--', xyeni, ykuvvet, '-')
plt.xlabel("x")
plt.ylabel("y")
plt.legend(['veri', 'lineer', 'kuvvet'], loc = 'best')
plt.plot
plt.show()
Bu yeni model her iki ekseni de logaritmik olarak ayarlanmak suretiyle doğru şeklinde de çizdirilebilir.
plt.plot(x, y, 'o', xyeni, ykuvvet, '-')
plt.xscale("log")
plt.yscale("log")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(['veri', 'kuvvet'], loc = 'best')
plt.plot
plt.show()
Polinom Regresyonu¶
Eğri uyumlamadaki temel yaklaşımı en küçük kareler minimizasyonu yöntemiyle görüldükten sonra aynı yaklaşımın polinom uyumlama için de kullanabileceği düşünülebilir. Doğada iki değişken arasındaki pek çok ilişki lineer ya da lineerleştirilebilir değildir. Bir polinomla temsil edilebilecek veri setleri için de uyumlanabilecek en iyi polinomun derecesini belirldikten sonra katsayılarını belirlemek üzere en küçük kareler minimizasyonu tercih edilebilir. Örneğin ikinci dereceden bir polinom (parabol) uyumlanmak istendiğinde model;
$$ y = a_0 + a_1~x + a_2~x^2 $$şeklinde ifade edilir. Yine minimize edilmek istenen parametre ($S_r$) verinin modelden fark karelerinin toplamıdır ve modelin hatasını (başarımının derecesini) sayısallaştırır.
$$ S_r = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_i + a_2 x_i^2))^2 $$Yine tipik bir minimizasyon problemi olan bu problemin çözümünde minimize edilmek istenen fonksiyonun ($S_r$), değişkenlerine ($a_0$, $a_1$, $a_2$) göre birinci türevi alınıp sıfıra eşitlenerek minimum değeri aranır. Fonksiyon ifadesindeki $x_i$, $y_i$ değerlerinin değişmez ölçümler olduğunu hatırlatmakta fayda vardır.
$$ \frac{\partial S_r}{\partial a_0} = -2 \sum_{i=1}^{n} (y_{i} - a_0 - a_1 x_i - a_2 x_i^2) $$$$ \frac{\partial S_r}{\partial a_1} = -2 \sum_{i=1}^{n} [(y_{i} - a_0 - a_1 x_i - a_2 x_i^2) x_i] $$$$ \frac{\partial S_r}{\partial a_2} = -2 \sum_{i=1}^{n} [(y_{i} - a_0 - a_1 x_i - a_2 x_i^2) x_i^2] $$ifadeleri 0'a eşitlenip düzenlendiğinde;
$$ (n)~a_0 + (\sum_{i=1}^{n} x_i) a_1 + (\sum_{i=1}^{n} x_i^2) a_2 = \sum_{i=1}^{n} y_{i} $$$$ (\sum_{i=1}^{n}x_i) a_0 + (\sum_{i=1}^{n} x_i^2) a_1 + (\sum_{i=1}^{n} x_i^3) a_2 = \sum_{i=1}^{n} x_{i} y_{i}$$$$ (\sum_{i=1}^{n}x_i^2) a_0 + (\sum_{i=1}^{n} x_i^2) a_1 + (\sum_{i=1}^{n} x_i^3) a_2 = \sum_{i=1}^{n} x_{i} y_{i}$$Çözülmesi gereken denklem sistemi budur. Bu denklem sistemini matris formunda ifade edecek olursak;
\begin{equation*} \begin{bmatrix} n & \Sigma x_i & \Sigma x_i^2 \\ \Sigma x_i & \Sigma x_i^2 & \Sigma x_i^3 \\ \Sigma x_i^2 & \Sigma x_i^3 & \Sigma x_i^4 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \Sigma y_i \\ \Sigma x_i y_i \\ \Sigma x_i^2 y_i \end{bmatrix} \end{equation*}Bu denklem $ R x A = M $ şeklinde bir lineer denklemdir ve çözümü oldukça kolaydır. Yapılması gereken, bilinmeyen katsayıları içeren $A = [a_0, a_1, a_2]$ matrisini yalnız bırakmak üzere denklemin her iki tarafını $R$ matrisinin tersi $R^{-1}$ ile çarpmaktır.
$$ R x A = M \Rightarrow R^{-1} x R x A = R^{-1} x M \Rightarrow I x A = R^{-1} x M \Rightarrow A = R^{-1} x M $$Genelleştirilmiş Çözüm:¶
Bu ifade genelleştirilerek herhangi bir dereceden polinom uyumlaması için aşağıdaki çözüm elde edilebilir.
$$ y = a_0 + a_1~x + a_2~x^2 + ... + a_m~x^m $$$$ S_r = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_i + a_2 x_i^2 + ... + a_m x^m))^2 $$olmak üzere;
\begin{equation*} \begin{bmatrix} n & \Sigma x_i & \Sigma x_i^2 & \cdots & \Sigma x_i^m \\ \Sigma x_i & \Sigma x_i^2 & \Sigma x_i^3 & \cdots & \Sigma x_i^{m+1} \\ \Sigma x_i^2 & \Sigma x_i^3 & \Sigma x_i^4 & \cdots & \Sigma x_i^{m+2} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \Sigma x_i^m & \Sigma x_i^{m+1} & \Sigma x_i^{m+2} & \cdots & \Sigma x_i^{2m} \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_m \end{bmatrix} = \begin{bmatrix} \Sigma y_i \\ \Sigma x_i y_i \\ \Sigma x_i^2 y_i \\ \vdots \\ \Sigma x_i^m y_i \end{bmatrix} \end{equation*}Daha sonra tıpkı kuadratik polinom (parabol) çözümünde olduğu gibi matris formunda ifade edilen bu lineer denklem aşağıdaki şekilde çözülür ve en iyi polinomun katsayıları elde edilir.
$$ R x A = M \Rightarrow R^{-1} x R x A = R^{-1} x M \Rightarrow I x A = R^{-1} x M \Rightarrow A = R^{-1} x M $$Örnek: Polinom Regresyonu¶
Aşağıdaki tabloda verilen veri setine uyan en iyi polinomu en küçük kareler minimzasyonu yöntemiyle belirleyerek veri seti üzerine bu polinomu çizdiriniz.
| $x_i$ | $y_i$ |
|---|---|
| 0 | 2.1 |
| 1 | 7.7 |
| 2 | 13.6 |
| 3 | 27.2 |
| 4 | 40.9 |
| 5 | 61.1 |
Öncelikle problemi yukarıdaki eşitliklerden yararlanarak kendi fonksiyonlarımızı yazmak suretiyle kendimiz çözelim.
import numpy as np
def parabol_uyumlama(x,y):
n = len(y)
Sxi = np.sum(x)
Sxi2 = np.sum(x**2)
Sxi3 = np.sum(x**3)
Sxi4 = np.sum(x**4)
Syi = np.sum(y)
Sxiyi = np.sum(x*y)
Sxi2yi = np.sum(x**2*y)
R = np.matrix([[n, Sxi, Sxi2], [Sxi, Sxi2, Sxi3], [Sxi2, Sxi3, Sxi4]])
M = np.matrix([[Syi],[Sxiyi],[Sxi2yi]])
Rinv = np.linalg.inv(R)
A = np.dot(Rinv,M)
return(A)
x = np.linspace(0,5,6)
y = np.array([2.1,7.7,13.6,27.2,40.9,61.1])
katsayilar = parabol_uyumlama(x,y)
print(katsayilar)
Görüldüğü gibi denklem takımı matris formuna getirilmek üzere numpy.matrix fonksiyonundan faydalanılmış ve her bir satırı birer liste olan listeler üzerinden matris formuna dönüştürülmüş oldu. $\Sigma x_i$, $\Sigma x_i^2$ gibi toplamların birden çok kez kullanılması gerektiği için onlara değişkenlere atamak iyi bir fikirdir. Daha sonra $R$ matrisinin tersini ($R^{-1}$) almak için numpy.linalg.inv fonksiyonu pratik olarak kullanılabilir. Sonrasında $R^{-1}~M$ matris çarpımı numpy.dot fonksiyonuyla yapılır. Burada iki önemli noktayı hatırlatmakta fayda var; birincisi iki matrisin doğrudan çarpımında ($R * M$) matrislerdeki karşılıklı elemanlar çarpıldığı için bunun bir matris çarpımı olmadığı, bunun ancak numpy.dot fonksiyonuyla yapılabildiği; ikincisi de burada sadece pedagojik olması açısından matris formundaki lineer denklem çözümünün adım adım ve büyük ölçüde manuel yapıldığı. Oysa ki numpy.linalg.solve() fonksiyonu kullanılarak bu amaca doğrudan da ulaşılabilir. numpy.linalg modülü lineer cebir uygulamaları için kullanılabilecek pek çok fonksiyon sağlaması bakımından oldukça kullanışlıdır.
import numpy as np
def parabol_uyumlama(x,y):
n = len(y)
Sxi = np.sum(x)
Sxi2 = np.sum(x**2)
Sxi3 = np.sum(x**3)
Sxi4 = np.sum(x**4)
Syi = np.sum(y)
Sxiyi = np.sum(x*y)
Sxi2yi = np.sum(x**2*y)
R = np.matrix([[n, Sxi, Sxi2], [Sxi, Sxi2, Sxi3], [Sxi2, Sxi3, Sxi4]])
M = np.matrix([[Syi],[Sxiyi],[Sxi2yi]])
A = np.linalg.solve(R,M)
return(A)
x = np.linspace(0,5,6)
y = np.array([2.1,7.7,13.6,27.2,40.9,61.1])
katsayilar = parabol_uyumlama(x,y)
print(katsayilar)
Bu kolaylık fonksiyonu sadece bir satır kısalttı ama bir miktar gereksiz iş yükünden de kurtardı. Bu tür durumlara programlar ve betiklerde dikkat edilmeli, Python ya da numpy, scipy gibi güvenilir paketlerdeki uygun fonksiyonlar ile yapabilabilecekler öğrenilip mümkün olduğunca ilgili fonksiyonlar kullanılmalıdır. Bu yaklaşım hem kodları hızlandıracak, hem de yazma, okuma ve dokümantasyon kolaylığı sağlayacaktır. Özünde $numpy$ ve $scipy$ fonksiyonlarını kullanarak parabol de uyumlayak mümkündür ama öğretici olması ve şeffaflık açısından bu örnekte katsayıların adım adım hesaplanması tercih edilmiştir. Şimdi uyumlanan parabol veri üzerine çizdirilerek görülebilir. Bir sonraki aşamada bu örnek bir de numpy.polyfit fonksiyonuyla çözülerek aynı sonuca ulaşılıp ulaşılmadığı denetlenebilir.
%matplotlib inline
from matplotlib import pyplot as plt
xyeni = np.linspace(0,5,50)
a0, a1, a2 = katsayilar
yparabol = float(a0) + float(a1)*xyeni + float(a2)*xyeni**2
plt.plot(x,y,'ro',label="veri")
plt.plot(xyeni,yparabol,'b-',label="model")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
Korelasyon katsayısı ($r^2$) ve tahmin üzerindeki standart hata ($S_{y/x}$) terimlerini hesaplamak için de bir fonksiyon yazalım ve uyumlamanın başarısını da sayısallaştıralım.
import numpy as np
def parabol_uyumlama_basarim(x,y,katsayilar):
n = len(y)
a0, a1, a2 = katsayilar
St = np.sum((y - y.mean())**2)
Sr = np.sum((y - (float(a0)+float(a1)*x+float(a2)*x**2))**2)
r2 = np.abs((St - Sr) / St)
Syx = np.sqrt(Sr / (n-2))
return(r2,Syx)
r2,Syx = parabol_uyumlama_basarim(x,y,katsayilar)
print("Verilen veriye uyumlanan en iyi parabol: y = {:.4f}x^2 + {:.4f}x + {:.4f}".\
format(float(a2),float(a1),float(a0)))
print("Korelasyon katsayisi r^2 = {:.4f}".format(r2))
print("Tahmin üzerindeki standart hata: {:.4f}".format(Syx))
Sy = np.sqrt(np.sum((y - y.mean())**2) / (len(y)-1))
print("Ortalama modelin standart sapması: {:.4f}".format(Sy))
Bu fonksiyonu parabol_uyumlama fonksiyonuyla birleştirmek ve uyumlamanın parametreleri (parabolün katsayıları) ile birlikte korelasyon katsayısı ve tahmin üzerindeki standart hatayı da bu fonksiyondan döndürmekte fayda vardır (deneyiniz!). Grafiği gördükten sonra anlamlı olmasa dahi, parabolik modelin ortalamaya göre ne oranda başarılı olduğunu göstermek üzere ortalama modelin standart sapması ile tahmin üzerindeki standart hata karşılaştırılabileceği gibi $r^2$ değerinin 1'e yakınlığına da bakılabilir.
numpy.polyfit İle Parabol Uyumlaması Örneği ve Uyumlamanın Başarısı¶
Aynı problemi daha önce de gördüğümüz numpy.polyfit fonksiyonundan yararlanarak çözelim. Bu kez fonksiyonu kullanırken $full$ parametresini $True$ değerine ayarlayarak çalıştıralım. Bu durumda sadece uyumlanan polinomun katsayılarını değil, aynı zamanda modelden artıkları ($S_r$), katsayılar matrisinin rank'ini, singüler olduğu değerleri, singüler değerlerin dikkate alınmayacağı limit değerini de verir. Bunlardan son üçü modelin hatasını hesaplarken işe yaramaz. Bu nedenle bu üç parametreyi "_" 'ye ayarlayarak kullanmayacağımızı belirtmiş olduk. Python'da birden fazla değer döndüren fonksiyonlarda kullanılmayacak değerler genellikle "_" değişkenine atanarak gözardı edilir. Ayrıca istenirse y değerlerinin ölçüm hataları da fonksiyona $w$ parametresi ile geçirilerek her bir noktanın hatası ile ($1 / e_i^2$) ağırlıklandırılmak suretiyle uyumlama yapılır. Bu durumda hatası büyük olan noktaya daha az ağırlık veirlmiş olur. Bu özellikten de faydalanmak ve veri üzerindeki deneysel (gözlemsel) hataların etkisini de değerlendirmek üzere veriye bir de hata sütun eklenmiştir.
| $x_i$ | $y_i$ | $e_i$ |
|---|---|---|
| 0 | 2.1 | 0.5 |
| 1 | 7.7 | 1.0 |
| 2 | 13.6 | 3.5 |
| 3 | 27.2 | 0.5 |
| 4 | 40.9 | 2.5 |
| 5 | 61.1 | 0.5 |
Ayrıca uyumlamanın başarısını göstermek için indirgenmiş $\chi^2$ parametresi de hesaplanarak çıktı olarak sağlansın. İndirgenmiş $\chi^2$ ("ki-kare" şeklinde okunur) parametresi aşağıdaki şekilde tanımlanır.
$$ \chi^2_\nu = \frac{\chi^2}{\nu} $$Burada sistemin $\nu$ serbestlik derecesi (dof, ing. degree of freedom), veri noktası sayısı ile model paramatreleri sayısı arasındaki farktır ($\nu = n - m$). $\chi^2$ parametresi ise gözlenen noktalar ile model arasındaki fark karelerinin varyansa (ya da noktanın hatasının karesine) oranlarının toplamıdır ve aşağıdaki şekilde verilir.
$$ \chi^2 = \sum_{i=1}^{n} \frac{(y - y_i)^2}{e_i^2} $$numpy.polyfit tarafından döndürülen artıklar, her bir noktanın hatasının $w$ parametresinden sağlanması durumunda aslında doğrudan $\chi^2$'ye eşittir. Zira verinin modelden fark kareler toplamı, noktanıın hatasının karesine bölünerek toplanması suretiyle hesaplanır. İndirgenmiş $\chi^2$ değerini bulmak için yapılması gereken sadece bu değeri serbestlik derecesine bölmektir.
$ \chi^2_\nu >> 1 $ olduğu durumda uyumlama oldukça başarısız ve veriyi temsil etmekten uzaktır. Genel olarak $ \chi^2_\nu > 1 $ olması, fitin veri üzerindeki belirsizliği tam olarak modelleyemediği anlamına gelir. Tüm noktalar uyumlanan eğri üzerinde değilse durum zaten bu olmalıdır. İndirgenmiş $ \chi^2_\nu = 1 $ ise gözlemler ile modelin, varyansla (ya da hatalarla) uyumlu bir şekilde örtüştüğü anlamına gelir. Bu durumda $\chi^2_\nu$'nin 1'e yakın olması, uyumlamanın (ya da modelin) da başarılı olduğu şeklinde yorumlanır. $\chi^2_\nu < 1$ durumu ise ancak modelden artıkların serbestlik derecesinden küçük olmasıyla mümkündür. Bu durum, verinin göstermediği kadar yüksek dereceden bir fonksiyonla uyumlandığı (ing. overfitting) ya da üzerindeki varyansın olduğundan fazla tahmin edildiği (ing. overestimated) şeklinde yorumlanır.
Örnek problemde nokta sayısı $n = 6$, modelin parametre sayısı $m = 3$ olduğundan (polinomun derecesi 2 iken parametre sayısı m = 3'tür), serbestlik derecesi ise $\nu = n - m = 6 - 3 = 3$ olur. Elde edilen indirgenmiş $\chi^2_\nu$ değeri 1'e yakın olup, parabolik modelin bu veri seti için kabul edilebilir, iyi bir model olduğunu göstermektedir.
Not: Model başarımı ve karşılaştırması için kullanılan diğer parametre ve testleri model karşılaştırması konusunda ayrıntılı olarak işlenecektir.
%matplotlib inline
import numpy as np
import math
from matplotlib import pyplot as plt
x = np.linspace(0,5,6)
y = np.array([2.1,7.7,13.6,27.2,40.9,61.1])
yerr = np.array([1.0,1.2,0.8,1.3,1.1,1.0])
# Sondaki 2, 2. dereceden polinomu gosterir.
# Agirliklandirmanin gozlemsel hatasi kucuk olan veri noktasina
# daha fazla agirlik verilerek yapilmasi icin w = 1 / yerr
katsayi,farkkare,_,_,_ = np.polyfit(x,y,deg=2,w=1/yerr,full=True)
# Parabol ifadesi
print("Veriye en iyi uyan parabol:")
print("{:.2f} x^2 + {:.2f} x + {:.2f}".format(katsayi[0],katsayi[1],katsayi[2]))
parabol = np.poly1d(katsayi)
xyeni = np.linspace(0,5) #varsayilan deger 50 noktadir
yparabolnumpy = parabol(xyeni)
plt.errorbar(x,y,yerr=yerr,c='r',fmt='.',label="veri")
plt.plot(xyeni,yparabolnumpy,'b-',label="model")
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
# Fit istatistikleri
Sr = farkkare[0] # farkkareler toplami bir dizi olarak verilir
St = np.sum((y - y.mean())**2)
r2 = np.abs((St - Sr) / St)
Syx = np.sqrt(Sr / (len(y) - 2))
nu = len(y) - len(katsayi) #serbestlik derecesi
chi2 = ((y - parabol(x))**2 / yerr**2).sum()
indChi2 = chi2 / nu
print("Korelasyon katsayisi r^2 = {:.4f}".format(r2))
print("Tahmin üzerindeki standart hata: {:.4f}".format(Syx))
print("Ki-kare: {:.4f}".format(chi2))
print("İndirgenmiş ki-kare: {:.4f}".format(indChi2))
Çok Değişkenli Lineer Regresyon¶
Astronomide ilgilenilen pek çok problemin tek bir değişkeni yoktur. Dolayısı ile modellemede birden fazla değişkene bağlılığın uyumlanması gerekir. Birden fazla değişkenin doğrusal bir modelinin elde edilmesi özünde tek değişkenli lineer regresyondan farklı değildir. Örneğin üç boyutta düşünecek olursak $x_1$ ve $x_2$ bağımsız değişkenleri göstermek üzere lineer bir model
$$ y = a_0 + a_1~x_1 + a_2~x_2 $$şeklinde ifade edilebilir. Yine minimize edilmek istenen parametre ($S_r$) verinin modelden fark karelerinin toplamıdır ve modelin hatasını (başarımının derecesini) sayısallaştırır.
$$ S_r = \sum_{i=1}^{n} (y_{i} - (a_0 + a_1 x_{1,i} + a_2 x_{2,i}))^2 $$Yine tipik bir minimizasyon problemi olan bu problemin çözümünde minimize edilmek istenen fonksiyonun ($S_r$), değişkenlerine ($a_0$, $a_1$, $a_2$) göre birinci türevi alınıp sıfıra eşitlenerek minimum değeri aranır. Fonksiyon ifadesindeki $x_{1,i}$, $x_{2,i}$ ve $y_i$ değerleri yine değişmez ölçümler olduğundan çözüm parabol uyumlamaya çok benzerdir.
$$ \frac{\partial S_r}{\partial a_0} = -2 \sum_{i=1}^{n} (y_{i} - a_0 - a_1 x_{1,i} - a_2 x_{2,i}) $$$$ \frac{\partial S_r}{\partial a_1} = -2 \sum_{i=1}^{n} [(y_{i} - a_0 - a_1 x_{1,i} - a_2 x_{2,i}) x_{1,i}] $$$$ \frac{\partial S_r}{\partial a_2} = -2 \sum_{i=1}^{n} [(y_{i} - a_0 - a_1 x_{1,i} - a_2 x_{2,i}) x_{2,i}] $$ifadeleri 0'a eşitlenip düzenlendiğinde;
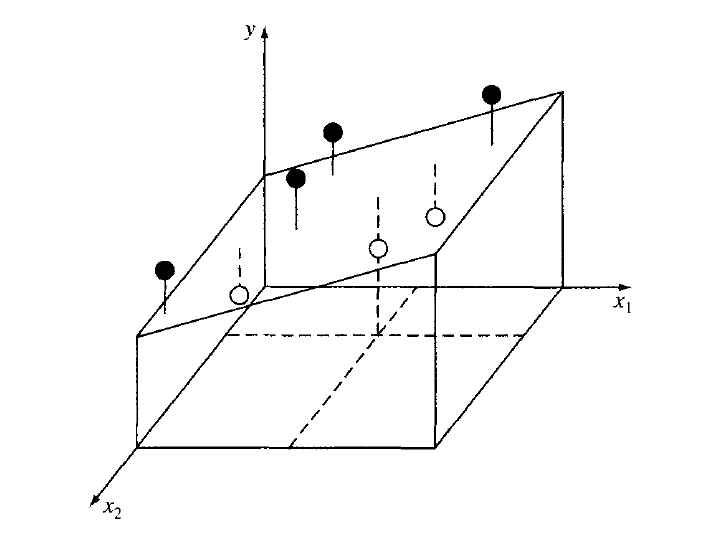
\begin{equation*} \begin{bmatrix} n & \Sigma x_{1,i} & \Sigma x_{2,i} \\ \Sigma x_{1,i} & \Sigma x_{1,i}^2 & \Sigma x_{1,i} x_{2,i} \\ \Sigma x_{2,i} & \Sigma x_{1,i} x_{2,i} & \Sigma x_{2,i}^2 \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \end{bmatrix} = \begin{bmatrix} \Sigma y_i \\ \Sigma x_{1,i} y_i \\ \Sigma x_{2,i} y_i \end{bmatrix} \end{equation*}Denklemin çözümü, birden fazla değişken olduğu için bir eğri (lineer modelde doğru) olmayıp, bir düzlem verecektir (aşağıdaki şekil). Şekilde görülen beyaz noktalar uyumlanan en iyi düzlemin altında, siyah noktalar ise üstünde kalan veri noktalarıdır. Dik doğrular modele (uyumlanan en iyi düzleme) uzaklıkları göstermektedir.
Örnek: Çok Değişkenli Lineer Regresyon¶
Diyelim ki aşağıdaki tabloda verilen veriye lineer bir model aranıyor olsun.
| $x_{1,i}$ | $x_{2,i}$ | $y_i$ |
|---|---|---|
| 0 | 0 | 5 |
| 2 | 1 | 10 |
| 2.5 | 2 | 9 |
| 1 | 3 | 0 |
| 4 | 6 | 3 |
| 7 | 2 | 27 |
import numpy as np
def duzlem_uyumlama(x1,x2,y):
n = len(y)
Sx1i = np.sum(x1)
Sx2i = np.sum(x2)
Sx1ix2i = np.sum(x1*x2)
Sx1i2 = np.sum(x1**2)
Sx2i2 = np.sum(x2**2)
Syi = np.sum(y)
Sx1iyi = np.sum(x1*y)
Sx2iyi = np.sum(x2*y)
R = np.matrix([[n, Sx1i, Sx2i], [Sx1i, Sx1i2, Sx1ix2i], [Sx2i, Sx1ix2i, Sx2i2]])
M = np.matrix([[Syi],[Sx1iyi],[Sx2iyi]])
A = np.linalg.solve(R,M)
return(A)
x_1 = np.array([0.0,2.0,2.5,1.0,4.0,7.0])
x_2 = np.array([0.0,1.0,2.0,3.0,6.0,2.0])
y = np.array([5.0,10.0,9.0,0.0,3.0,27.0])
katsayilar = duzlem_uyumlama(x_1,x_2,y)
print(katsayilar)
Uyumlanan düzlem ve veriyi 3-boyutlu bir grafik üzerinde göstermek için plt.scatter3D fonksiyonundan faydalanılabilir.
%matplotlib inline
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure(figsize=(12,8))
ax = fig.gca(projection='3d')
# Veri noktalarini cizdirme
ax.scatter3D(x_1, x_2, y, color="r", marker="o", s=50)
# Duzlem cizdirme
X1, X2 = np.meshgrid(x_1, x_2)
a0,a1,a2 = katsayilar
Y = float(a0) + float(a1)*X1 + float(a2)*X2
ax.plot_surface(X1, X2, Y, color="gray", alpha=0.5, rstride=1)
ax.set_xlabel("$x_1$")
ax.set_ylabel("$x_2$")
ax.set_zlabel("$y$")
plt.show()
Çok Değişkenli Lineer Regresyon: Genel İfade¶
Çok değişkenli doğrusal regresyonu iki değişken örneği üzerinden gördük. İfadeyi $m$ sayıda değişkene genelleştirmek istersek yukarıdaki ifadeleri aşağıda verildiği şekliyle değiştirmemiz gerekir.
$$ y = a_0 + a_1~x_1 + a_2~x_2 + ... + a_m~x_m $$şeklinde ifade edilebilir. Yine minimize edilmek istenen parametre ($S_r$) verinin modelden fark karelerinin toplamıdır ve modelin hatasını (başarımının derecesini) sayısallaştırır.
$$ S_r = \sum_{i=1}^{n} (y_{i} - a_0 - a_1 x_{1,i} - a_2 x_{2,i} - ... - a_m x_{m,i})^2 $$Yine tipik bir minimizasyon problemi olan bu problemin çözümünde minimize edilmek istenen fonksiyonun ($S_r$), değişkenlerine ($a_0$, $a_1$, $a_2$, ... , $a_m$) göre birinci türevi alınıp sıfıra eşitlenerek minimum değeri aranır. Fonksiyon ifadesindeki $x_{1,i}$, $x_{2,i}$, ..., $x_{m,i}$ ve $y_i$ değerleri yine değişmez ölçümler olduğundan çözüm parabol uyumlamaya çok benzerdir. Sonuçta aşağıda matris formunda ifade edilen lineer denklem sistemi elde edilmiş olur ve bu sistem çözülerek en iyi modelin parametreleri elde edilir.
\begin{equation*} \begin{bmatrix} n & \Sigma x_{1,i} & \Sigma x_{2,i} & \cdots & \Sigma x_{m,i} \\ \Sigma x_{1,i} & \Sigma x_{1,i}^2 & \Sigma x_{1,i} x_{2,i} & \cdots & \Sigma x_{1,i} x_{m,i} \\ \Sigma x_{2,i} & \Sigma x_{1,i} x_{2,i} & \Sigma x_{2,i}^2 & \cdots & \Sigma x_{2,i} x_{m,i} \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ \Sigma x_{m,i} & \Sigma x_{1,i} x_{m,i} & \Sigma x_{2,i} x_{m,i} & \cdots & \Sigma x_{m,i}^2 \\ \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ a_2 \\ \vdots \\ a_m \end{bmatrix} = \begin{bmatrix} \Sigma y_i \\ \Sigma x_{1,i} y_i \\ \Sigma x_{2,i} y_i \\ \vdots \\ \Sigma x_{m,i} y_i \\ \end{bmatrix} \end{equation*}En Küçük Kareler Minimizasyonu Yöntemi Genel İfade¶
En küçük kareler minimizasyonu yöntemi gördüğünüz gibi değişken sayısı ve uyumlanan fonksiyonun derecesi ya da parametre sayısından bağımsız olarak benzer bir yol izlemektedir. Bu benzer yol aşağıdaki genel ifadenin elde edilmesini ve bu şekilde en küçük kareler minimizasyonunun tüm durumalr için tek bir ifadeyle verilmesini sağlar.
$$ y = a_0 ~z_0 + a_1~z_1 + a_2~z_2 + ... + a_m~z_m $$Bu ifade
$ z_0 = 1, z_1 = x, z_2 = .. = z_m = 0 $ için 1-boyutlu lineer regresyon, $ z_0 = 1, z_1 = x_1, z_2 = x_2, ... , z_m = x_m $ için m-boyutlu lineer regresyon, $ z_0 = 1, z_1 = x, z_2 = x^2, ... , z_m = x^m $ için m. dereceden polinom regresyonuna
karşılık gelir. Çözüm her zaman aynı şekilde aranır.
$$ Z x A = y $$şeklinde matris formunda verilen denklem sisteminde
\begin{equation*} [Z] = \begin{bmatrix} z_{01} & z_{11} & \cdots & z_{m1} \\ z_{02} & z_{12} & \cdots & z_{m2} \\ \vdots & \vdots & \ddots & \vdots \\ z_{0n} & z_{1n} & \cdots & z_{mn} \end{bmatrix} \begin{bmatrix} a_0 \\ a_1 \\ \vdots \\ a_m \end{bmatrix} = \begin{bmatrix} y_1 \\ y_2 \\ \vdots \\ y_n \\ \end{bmatrix} \end{equation*}$A$ katsayılar matrisinin bulunabilmesi için $Z$ matrisinin tersi ($Z^{-1}$) alınır ve her iki taraf sol taraftan $Z^{-1}$ matrisi ile çarpılır. Sonuç $A = Z^{-1} Y$ matrisidir.
Korelasyon katsayısı: $$ r^2 = \frac{S_t - S_r}{S_t} = 1 - \frac{S_t}{S_r} $$
$S_t$ aritmetik ortalama ($\bar{y} = \frac{\Sigma y_i}{n}$) model olarak kabul edildiğinde ondan fark karelerin toplamı, $S_r$, en küçük kareler minimizasyonu tekniğiyle elde edilen modelden ($\hat{y}$) fark karelerin toplamını göstermek üzere;
$$ r^2 = 1 - \frac{\Sigma (y_i - \hat{y_i})^2}{\Sigma (y_i - \bar{y_i})^2} $$ile verilir.
Tahmin üzerindeki standart hata:
$$ S_{y/x} = \sqrt{\frac{\Sigma (y_i - \hat{y_i})^2}{n - (m+1)}} $$$\chi^2$:
$$ \chi^2 = \sum_{i=1}^{n} \frac{(\hat{y_i} - y_i)^2}{e_i^2} $$olmak üzere indirgenmiş $\chi^2_\nu$:
$$ \chi^2_\nu = \frac{\chi^2}{(n - m)} $$ile verilir.
Doğrusal Olmayan En Küçük Kareler Yöntemi¶
Levenberg Marquardt Algoritması¶
Matematik ve bilgisayar bilimlerinde Levenberg-Marquardt Algoritması (LMA) , sönümlenmiş en küçük kareler yöntemi (Damped Least Squares, DLS) olarak da bilinir. m adet gözlemsel veriyi n tane bilinmeyenle modellemek üzere başlangıçta doğrusal bir model üretilip, modelin iterasyonlar sonucu iyileştirilerek doğrusal olmayan bir modelle değiştirilmesi prensibine dayanır.
$(x_0, y_0)$, $(x_1, y_1)$, $(x_2, y_2)$, … , $(x_m, y_m)$ gözlemsel noktalarımız olsun. Bu noktaları $f(x, \beta)$ gibi bir fonksiyonla uyumlamak (fit etmek) istiyor olalım. Burada $m \ge n$ olmak üzere $\beta = (\beta_0, \beta_1, … , \beta_{n-1}$) fonksiyonun parametreleridir ve fonksiyon $x$ ile birlikte bu parametrelere de bağlıdır. Algoritmada amaç en küçük kareler yöntemine benzer şekilde en küçük artıkları verecek $S_r = \Sigma (y_i - f(x_i, \beta))^2$ minimizasyonunun gerçekleşeceği $\beta$ parametrelerini elde etmektir.
Tıpkı en küçük kareler yönteminde olduğu gibi yine $S_r$'nin bu kez $\beta_j$ ($j = 0, 1, 2, … , n$) adını alan fit fonksiyonu parametrelerine göre türevleri alınır ve 0'a eşitlenir. Doğrusal olmayan bir sistemde bu türevler hem $x$'e hem de $\beta$'ya bağlı olacağından doğrudan çözüm elde etmek yerine probleme uygun seçilmiş başlangıç parametreleri ile başlanır ($\beta$'lara başlangıç değerleri verilir) ve iteratif bir yaklaşımla her seferinde $S_r$ hesaplanıp, daha öncekilerle ile karşılaştırılarak en küçük $S_r$'yi verecek parametre seti aranır. $\beta$ her seferinde $\beta + \delta$ ile değiştirilir. $\delta$'yı bulmak için $f(x_i, \beta + \delta)$ doğrusallaştırılmak üzere Taylor serisine açılır ($f(x_i, \beta + \delta) ≈ f(x_i, \beta) + J_i\delta$, $J_i$: Jakobiyen). $S_r$'nin $\beta$'ya görevi türevi 0 olduğunda $S_r(\beta + \delta) = \Sigma (y_i – f(x_i, \beta) – J_i\delta)^2$ toplamının $\delta$'ya göre türevi de 0 olmalıdır ki minimizasyon sağlanmış olsun. Vektörel notasyonla ($J^T J) \delta = J^T |(y_i – f(\beta)|$ denklemi $\delta$ için çözülür ve $\beta$ parametreleri bulunur.
Levenberg'in algoritmaya getirdiği yenilik bir sönümleme (ing. damping) parametresi eklemiş olmasıdır. Böylece denklem ($J^T J + \lambda I) \delta = J^T |(y_i – f(\beta)|$ şeklini alır. Sönümleme parametresi $\lambda$, her bir iterasyon adımında değiştirilir ve $\beta + \delta$ 'nın belirenen bir tolerans değerinin altına indiği anda iterasyon durdurulur. En son $\beta$ vektörü fonksiyonun parametrelerini verir.
Doğrusal olmayan (non-lineer) en küçük kareler problemini çözmek üzere geliştirilmiş tek yöntem Levemberg-Marquardt algoritması değildir. [Trust Region Reflective Algorithm](https://nmayorov.wordpress.com/2015/06/19/trust-region-reflective-algorithm/) ya da bu algoritmanın varyantları olan dogleg ve Steihaug algoritmaları da doğrusal olmayan en küçük kareler probleminin çözümünde kullanılmaktadır.
Levenberg-Marquardt Algoritmasına Yönelik Bazı Uyarılar:¶
Her ne kadar sık kullanılsa da doğrusal olmayan en küçük kareler minimizasyonu probleminin çözümünde Levenberg-Marquardt algoritmasına yönelik olarak aşağıdaki uyarılar dikkate alınmalıdır:
Algoritma verilen başlangıç parametrelerine en yakın yerel minimumu bulması nedeniyle dezavantajlıdır.
Bir süre benzer (ya da yakın) değerler alan fonksiyonlarda minimizasyon konusunda problemlidir (bu noktalarda zig-zag yapar!).
Bazı durumlarda (başlangıç parametrelerinin çözüme yakınlığı) oldukça hızlı çalışırken, bazı durumlarda en iyi fiti verecek parametreleri bulmak konusunda oldukça yavaş olabilir.
scipy.optimize.leastsq ile Uyumlama¶
scipy.optimize modülü eğri uyumlama için pek çok fonksiyon ve alt modül sağlar. leastsq bu fonksiyonlardan biridir ve doğrusal olmayan (non-lineer) en küçük kareler problemini çözerek verilen veriye uyan en iyi eğriyi bulur. Buna ek olarak scipy.optimize paketi sadece Levenberg-Marquardt algoritmasıyla değil, Trust Region Reflective algoritması ve dogleg algoritmasıyla da çözüm arayabilen least_squares adlı bir başka fonksiyonu daha içermektedir. Bu fonksiyonda çözüm için istenen algoritma, $method$ parametresi sırasıyla $lm$, $trf$ ya da $dogbox$ değerlerine ayarlanarak seçilebilir. Klasik en küçük kareler yönteminden farklı olarak daha hızlı çalışır ve yerel minimumlara saplanma olasılığı daha azdır. Ayrıca her iki fonksiyonla sadece doğru, parabol ya da istenen dereceden başka bir polinom değil, istenen her türden fonksiyon uyumlanabilir.
scipy.optimize.leastsq fonksiyonunun kullanılışını örneklemek üzere aşağıdaki kodun başında $x$ ve $y$ numpy dizileriyle verilen veri setine Levenberg-Marquardt algoritmasıyla bir doğru bir de Parabol fit edilmek isteniyor olsun. Yapılması gereken leastsq fonksiyonuna gözlemsel $(x,y)$ değerleri ile hesaplananlar arasındaki hatayı veren bir Hata Fonksiyonu (ing. error function), birer başlangıç parametre seti, $a_0 + a_1 x$ doğrusu için $\beta = (\beta_0, \beta_1) = (a_0, a_1)$ parametreleri, $a_0 + a_1 x + a_2 x^2$ parabolü için $\beta = (\beta_0, \beta_1, \beta_2) = (a_0, a_1, a_2)$ parametreleri olarak sırasıyla $(1.0, 2.0)$ ve $(1.0, 2.0, 3.0)$, ve veri setini $(args = (x,y))$ içeren fonksiyon argümanlarını vermektir. Levenberg-Marquardt algoritması bu parametreler için en iyi değerleri hesaplar ve bu parametreler doğru ve parabol denklemlerinde yerine konarak istenen uyumlamalar yapılmış olur.
%matplotlib inline
from scipy.optimize import leastsq
import numpy as np
import matplotlib.pyplot as plt
# veri
x=np.array([1.0,2.5,3.5,4.0,1.1,1.8,2.2,3.7])
y=np.array([6.008,15.722,27.130,33.772,5.257,9.549,11.098,28.828])
# Dogru ve Parabol fitleri icin birer lamda fonksionu yaratalim
# beta burada fitin parametrelerini (a0, a1, <a2>) tutan bir demet degisken
fonkDogru = lambda beta,x : beta[0]*x+beta[1]
fonkParabol = lambda beta,x : beta[0]*x**2+beta[1]*x+beta[2]
# fonk fit etmek istedigimiz fonksiyonun yerini alsin
# Bunu istedigimiz gibi degistirebiliriz.
#------------------------------------------------
# Dogrusal Fit
#-------------------------------------------------
fonk = fonkDogru
# HataFonksiyonu, fit fonksiyonumuzla hesaplanan y ile gozlemsel y arasindaki
# farki versin (toplami S)
HataFonksiyonu = lambda beta,x,y: fonk(beta,x)-y
# tplBaslangicD Levenberg-Marquard algoritmasini baslatmak icin baslangic
# parametre setimiz (beta), dogrusal oldugunu gostermek uzere D kullandim
# beta parametre seti a0 (sabit) ve a1 (egim)'den olusuyor --> a0 + a1*x
beta_baslangicD = (1.0,2.0)
# scipy.optimize.leastsq baslangicD ile baslatilan beta parametre setinin
# HataFonksiyonu toplamini (Sr) veren degerlerini bulur
# HataFonksiyonu = yfit - yIterasyon
beta_sonD,_ = leastsq(HataFonksiyonu,beta_baslangicD[:],args=(x,y))
print(" Linear Fit ",beta_sonD)
xxD=np.linspace(x.min(),x.max(),50)
yyD=fonk(beta_sonD,xxD)
#------------------------------------------------
# Parabol Fiti
#-------------------------------------------------
fonk = fonkParabol
beta_baslangicP = (1.0,2.0,3.0)
beta_sonP,_ = leastsq(HataFonksiyonu,beta_baslangicP[:],args=(x,y))
print("Parabol Fiti: " ,beta_sonP)
xxP = xxD
yyP = fonk(beta_sonP,xxP)
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y,'ro',label="veri")
plt.plot(xxD,yyD,'b-',label="dogru")
plt.plot(xxP,yyP,'g-',label="parabol")
plt.legend(loc="best")
plt.show()
scipy.optimize.curve_fit ile Uyumlama¶
Tıpkı scipy.optimize.least_squares gibi curve_fit fonksiyonu da doğrusal olmayan en küçük kareler minimizasyonu problemini çeşitli yöntemlerle çözer. Yapısı ve uygulama şekli ona oranla biraz farklı ve daha esnektir.
Bu fonksiyonun kullanımını örneklemek için bu kez doğru ya da parabol uyumlamadan farklı bir fonksiyon (üstel fonksiyon) seçilmiştir. Bu amaçla öncelikle üstel fonksiyonla uyumlanabilecek sentetik bir veri seti oluşturmak üzere aşağıdaki fonksiyon yazılmıştır. Öncelikle $[0,4]$ arasında 50 nokta içeren $x$ dizisi $y = 2.5 e^{-1.3x} + 0.5$ fonksiyonuna (veri_olusturma) sağlanarak bir $y$ dizisi oluşturulmakta, daha sonra rastgele gürültü eklemek üzere bu dizi numpy.random.normal fonksiyonu ile normal (Gaussyen) bir dağılımdan rastgele örneklemeyle oluşturulan y_gurultu dizisiyle toplanmaktadır.
import numpy as np
veri_olusturma = lambda x,a,b,c: a * np.exp(-b * x) + c
x = np.linspace(0,4)
y = veri_olusturma(x,2.5, 1.3, 0.5)
# Veri setimize biraz Gaussyen (normal dagilan) gurultu ekleyelim
np.random.seed(1729)
y_gurultu = 0.2 * np.random.normal(size=x.size)
y += y_gurultu
Oluşturulan sentetik veri setini curve_fit fonkisyonuyla uyumlamak üzere fonksiyona uyumlayacağı fonksiyonun türü ve veri argüman olarak sağlanır. Uyumlamak istenen fonksiyon üstel bir fonksiyon olduğu için aslında sentetik veri oluşturmak için kullanılan $lambda$ fonksiyonuyla (veri_olusturma) aynı fonksiyon olacaktır. O nedenle yeni bir fonksiyon oluşturulmak yerine bu fonksiyon sağlanabilir. curve_fit bu durumda sentetik veri için en iyi $a$, $b$ ve $c$ değerlerini bulur. Bu değerlerin aslında sırasıyla $2.5$, $1.3$ ve $0.5$'e yakın olması beklendiğinden karşılaştırma da yapılabilir. Ancak veriye gürültü de eklediğinden curve_fit tarafından bulunan değerler doğal olarak tam olarak aynı çıkmamalıdır.
%matplotlib inline
from scipy.optimize import curve_fit
from matplotlib import pyplot as plt
param, kovar = curve_fit(veri_olusturma, x, y)
print("Veriye uyumlamanan ustel fonksiyonun parametreleri: ", param)
a = float(param[0])
b = float(param[1])
c = float(param[2])
print("Model: {:.2f} e^(-{:.2f}x) + {:.2f}".\
format(a,b,c))
plt.plot(x,y,'ro',label="veri")
y_model = a*np.exp(-b*x) + c
plt.plot(x, y_model,'b-',label='model')
plt.legend(loc="best")
plt.show()
LMFIT Paketiyle Modelleme¶
Levenberg-Marquardt algoritmasıyla daha sofistike ve esnek uyumlamalar için geliştirilmiş olan LMFIT paketi, scipy.optimize modülü üzerine kurulu ve onun optimizasyon ve eğri uyumlama yeteneklerini daha ileriye taşıyan bir pakettir. İndirmek, kurmak ve kullanımı için bkz..
Aşağıda önce scipy.optimize.curve_fit fonksiyonu kullanılarak çözülen bir uyumlama problemi örneklenmiştir. Öncelikle $[-10,10]$ aralığında 50 nokta içeren bir $x$ dizisi numpy.linspace fonksiyonuyla oluşturulmaktadır. Daha sonra sentetik veriyi oluşturmak için bu dizi $gauss$ fonksiyonuna $A = 2.33$ genlik, $\mu = 0.21$ ortalama değer, $\sigma = 1.51$ standart sapma değerleriyle gönderilmekte ve $y = A e^{-(x-\mu)^2 / (2\sigma)}$ fonksiyonuyla sentetik y verisi oluşturulmaktadır. Daha sonra bu veriye ortalma değeri 0.0, standart sapması 0.2 olan bir Gauss dağılımından rastgele seçilen 50 değer eklenmekte, bu şekilde veri üzerinde sentetik bir gürültü (saçılma) oluşturulmaktadır.
Bu veri scipy.optimize.curve_fit fonksiyonuyla yine daha önceki gibi veriyi oluşturmak için kodlanan gauss fonksiyonu ile birlikte sağlanarak modellenmek istenmektedir. Gauss fonksiyonunun başlangıç parametreleri $A = 1.0$, $\mu = 0.0$, $\sigma = 1.0$ olarak seçilmiştir. Bu parametrelerin fit sonunda $A = 2.33$, $\mu = 0.21$ ve $\sigma = 1.51$ değerlerine yakınsamasını beklenir; zira bu veri bu değerler kullanılarak fit için de kullanılan gauss fonksiyonuyla oluşturulmuştur.
import numpy as np
from scipy.optimize import curve_fit
def gauss(x, genlik, ortalama, stsapma):
return genlik*np.exp(-(x-ortalama)**2/(2*stsapma))
x = np.linspace(-10, 10)
y = gauss(x, 2.33, 0.21, 1.51) + np.random.normal(0, 0.2, len(x))
baslangicPar = [1, 0, 1]
param, kovar = curve_fit(gauss, x, y, p0 = baslangicPar)
print("Veriye uyumlamanan ustel fonksiyonun parametreleri: ", param)
A = float(param[0])
mu = float(param[1])
sigma = float(param[2])
print("Model: {:.2f} e^(-(x-{:.2f}) / 2*{:.2f})".\
format(A,mu,sigma))
x2 = np.linspace(-10,10,100)
yfit = param[0]*np.exp(-(x2 - param[1])**2/param[2])
plt.plot(x,y,'ro',label="veri")
plt.plot(x2,yfit,'b-',label="model")
plt.legend(loc="best")
plt.show()
Görüldüğü gibi bulunan değerler veriyi oluşturmak için kullanılan değerlere yakındır. Yani scipy.optimize.curve_fit iyi bir sonuç vermiş görünmektedir. Ancak uyumlama süreci hem şeffaf değil, hem de uyumlamaya ilişkin bazı istatistiksel parametrelerin kullanıcı tarafından hesaplanmasına ihtiyaç duyulmaktadır. LMFIT paketi Model gibi çok kullanışlı bir metot sağlar. Bu metodun ürettiği modelin parametrelerinin sırasının bilinmesi gerekmez, adlarının bilinmesi yeterlidir. Model fonksiyonuna, veriyi hem oluşturmak hem de modellemek üzere kullanılan gauss fonksiyonu sağlanarak fit işlemi daha şeffaf ve pratik bir hale getirilebillir.
import lmfit as lm
gmodel = lm.Model(gauss)
print(gmodel.param_names)
print(gmodel.independent_vars)
Görüldüğü gibi modelin parametreleri gauss fonksiyonunun parametreleri; bağımsız değişkeni de $x$ 'tir. Model veriye uyumlandıktan (fit edidikten) sonra parametreleri fit_report fonksiyonuyla incelenebilir
sonuc = gmodel.fit(y, x=x, genlik=1, ortalama=0, stsapma=1)
print(sonuc.fit_report())
LMFIT dokümantasyoundan da anlaşılacağı üzere oldukça gelişmiş bir uyumlama ortamı sunar. Uyumlama temel parametrelerle yapıldığında görece kolay olmakla birlikte LMFIT pek çok başka girdi parametresine daha sahiptir ve bu opsiyonel parametreler uyumlama için oldukça esnek bir yapı sunar. Tüm bu detaylar dokümantasyon yoluyla öğrenilip, gereğince kullanılmalıdır. Ancak bu aşamada bu detay düzeyiyle yetinilecektir. fit_report() fonksiyonunun sağladğı rapor parametrelerine bakıldığında model parametrelerinin değerleri ve hatalarının (yüzde düzeyleriyle birlikte) yanı sıra $\chi^2$, indirgenmiş $\chi^2_\nu$ (reduced chi-square) gibi uyumlamanın başarısını gösteren istatistiklerle birlikte Akaike ve Bayesian ölçütleri gibi model karşılaştırması dersinde işlenecek diğer parametrelerin değerleri de görülmektedir.
Modeli veri üzerinde göstermek üzere, sonuc nesnesinin best_fit, başlangıç parametreleriyle, oluşan modele ise init_fit metoduyla ulaşılabilir. Diğer taraftan uyumlama parametrelerinin değerleri params sözlüğünün ilgili parametreye karşılık gelen anahtarının value metoduyla alınabilir.
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(x, y, 'ro', label="veri") # veri
plt.plot(x, sonuc.init_fit, 'b--', label="başlangic modeli") # A=1, mu=0, sigma=1 icin fit
plt.plot(x, sonuc.best_fit, 'g-', label="sonuc model") # Veri setine uyumlanan en iyi fit
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
# Fitimizin parametrelerini ekrana yazdiralim
print("En iyi uyumlamanin genligi = {:.2f}, ortalama degeri = {:.2f}, st.sapma = {:.2f}".\
format(sonuc.params['genlik'].value,sonuc.params['ortalama'].value,sonuc.params['stsapma'].value))
Örnek: Küresel Isınmanın Ciddiyeti¶
Karbondioksit seviyesinde 1960'dan bu yanaki değişim Keeling Eğrisi adı verilen bir eğriyle ifade edililr. Söz konusu değişim küresel ısınmaya neden olduğu gerekçesiyle endişe konusudur. Aşağıda 1960'dan bu yana geçen süre içerisinde onar yıllık ölçüm sonuçları milyon parçacık başına verilmiştir. Keeling Eğrisinin bir parabolle (2. dereceden bir polinomla) temsil edilebileceğini düşünerek ve eldeki veriyi kullanarak eğriye en uygun formülü bulunuz. Keeling Eğrisi yapısını korursa 2030 yılı sonunda parçacık başına kaç karbondioksit molekülü düşer hesaplayınız.
| Yıl | $CO_2$ |
|---|---|
| 0 | 317 |
| 10 | 326 |
| 20 | 338 |
| 30 | 354 |
| 40 | 369 |
| 50 | 390 |
Öncelikle verimizi bir grafiğe döküp nasıl bir modelle veriyi en iyi uyumlayabileceğimizi düşünelim.
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
t = np.arange(0,51,10.)
CO2 = np.array([317,326,338,354,369,390])
plt.plot(t,CO2,'ro')
plt.show()
Değişim lineer gibi gözükse de bir miktar eğiklik kendini hissettirdiğinden öncelikle bir parabolik model ($a_0 + a_1~x + a_2~x^2$) varsayalım. Daha önce olduğu gibi modelimizin parametrelerini bir görelim.
import lmfit as lm
parabol = lambda x,a0,a1,a2: a0 + a1*x + a2*x**2
parmodel = lm.Model(parabol)
print(parmodel.param_names)
print(parmodel.independent_vars)
Modelimizin ($parmodel$) üç parametresi ($a_0$, $a_1$ ve $a_2$) ve bir de bağımsız değişkeni ($x$) var. Şimdi bu modeli verimize fit etmek üzere modelimiz ($parmodel$) üzerinde tanımlı fit metodunu kullanalım. Metoda verimizi önce $y = CO2$, sonra $x = t$ ile verdiğimize ve başlangıç parametresi olarak da göz kararı belirlediğimiz $a_0 = 300$, $a_1 = 2$ ve $a_2 = 1$ değerlerini argüman olarak verdiğimize dikkat ediniz. Uyumlama sonucunu $sonucpar$ değişkenine alıyoruz. Bu değişken bir $lmfit$ model sonucu nesnesi olarak böylece tanımlanmış oluyor. Bu nesnenin uyumlamaya ilişkin istatistiksel bilgileri alabileceğiniz bir fit_report() metodu ve parametrelerini almanız için de params adında bir sözlük değişkeni tanımlı. Öncelikle uyumlamaya ilişkin istatistiksel bilgileri görelim.
sonucpar = parmodel.fit(CO2, x=t, a0 =300, a1=2, a2=1)
print(sonucpar.fit_report())
Bu bilgilerden özellikle $\chi^2$ ve indirgenmiş $\chi^2_\nu$ istatistiğinin uyumlama başarısını göstermekte kullanıldığını hatırlayalım. Akaike ve Bayes parametreleri de uyum başarısını verir ancak bu parametrelerin nasıl tanımlandığını daha sonra model karşılaştırmasına yönelik dersimizde göreceğiz. Ayrıca parametrelerimize ilişkin değerler, korelasyon katsayıları ve hataları da raporda sunulmuş durumdadır. Şimdi modelimizi verimizin üzerine çizdirelim.
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(t, CO2, 'ro', label="veri") # veri
plt.plot(t, sonucpar.init_fit, 'b--', label="başlangic modeli") # a0=300, a1=2, a2=1
plt.plot(t, sonucpar.best_fit, 'g-', label="sonuc model") # Veri setine uyumlanan en iyi fit
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
# Fitimizin parametrelerini ekrana yazdiralim
print("En iyi uyumlama: {:.2f} + {:.2f}x + {:.2f}x^2".\
format(sonucpar.params['a0'].value,sonucpar.params['a1'].value,sonucpar.params['a2'].value))
Görüldüğü üzere başlangıç parametreleriyle oluşturulan eğri (mavi kesikli) verimizi uyumlamaktan uzakken, lmfit 'in bu başlangıç parametrelerinden hareketle uyumladığı parabol (yeşil sürekli) başarılı görünmektedir. $a_2$ katsayısının değerinin $0.01$ olarak bulunmuş olması bize doğrusal bir modelin de belki başarılı olacağını düşündürtebilir. Bunun için verimize bir de doğru modeli uyumlamaya çalışalım. Bu kez iki parametreli bir doğru fonksiyonu ($dogru$) tanimlayacağız ve bunu bir lmfit modeline Model fonkisyonuyla dönüştüreceğiz.
dogru = lambda x,a0,a1: a0 + a1*x
dogrusalmodel = lm.Model(dogru)
print(dogrusalmodel.param_names)
print(dogrusalmodel.independent_vars)
Ardından modelimizin doğrusal olmayan en küçük kareler yöntemlerinden Levenberg-Marquardt algoritmasıyla uyumlanması sonucunda oluşan en iyi modelimize ilişkin parametreleri sonuc_dogrusal model sonucu değişkenine alalım ve sonuç modelimizin parametrelerini görelim.
sonuc_dogrusal = dogrusalmodel.fit(CO2, x=t, a0 =300, a1=1.0)
print(sonuc_dogrusal.fit_report())
Gördüğünüz gibi $\chi^2_\nu >> 1$ durumu oluşmakta, doğru modelin parabole göre verinin üzerindeki belirsizliği açıklamakta daha başarısız olduğu görünmektedir. Ancak her iki modeli bir de grafik üzerinde karşılaştıralım. Gelecek derste model karşılaştırmasına yönelik olarak yapılması gerekenleri ayrıntılı olarak göreceğiz.
%matplotlib inline
from matplotlib import pyplot as plt
plt.plot(t, CO2, 'ro', label="veri") # veri
plt.plot(t, sonucpar.best_fit, 'b--', label="parabol modeli") # a0=300, a1=2, a2=1
plt.plot(t, sonuc_dogrusal.best_fit, 'g-', label="dogrusal model") # Veri setine uyumlanan en iyi fit
plt.xlabel("x")
plt.ylabel("y")
plt.legend(loc="best")
plt.show()
# Fitimizin parametrelerini ekrana yazdiralim
print("En iyi uyumlama: {:.2f} + {:.2f}x".\
format(sonuc_dogrusal.params['a0'].value,sonuc_dogrusal.params['a1'].value))
Eğri Uyumlamanın İnterpolasyon ve Ekstrapolasyon Amacıyla Kullanımı¶
Bir matematiksel ya da fiziksel model, bağımsız bir değişkenin herhangi bir değeri için bağımlı değişkene ilişkin bir sonuç vereceği için interpolasyon ya da ekstrapolasyon amacıyla da kullanılabilir. Örneğimizde atmosferimizdeki milyon parçacık başına $CO_2$ molekülü sayısının Keeling eğrisiyle artması koşuluyla gelecekte alabileceği değerleri ya da 1960'dan önceki değerlerini hesaplamak isteyebiliriz. Eldeki veriden yola çıkarak gelecek ve geçmişe yapılan bu projeksiyon ekstrapolasyon olarak bilinir. Bilimde "tehlikeli" bir işlem olmakta birlikte sıklıkla uygulanır. Tehliklesi verinin alındğı aralıktaki fonksiyonun gelecek ve geçmiş için de geçerli olup olmayacağının bilinmemesidir. Diğer taraftan verinin alındığı aralıkta bulunan ancak veri noktasının bulunmadığı bir nokta için de hesap yapılabilir. Daha önce çeşitli yöntemlerini gördüğünüz bu yöntem interpolasyon olarak bilinir ve eğri uyumlamayla elde edilen bir matematiksel model interpolasyon amacıyla da kullanılabilir.
Örneğimizden hareketle 2030 ve 2005 yılları için atmosferimizdeki milyon parçacık başına, parabolik modelimizin kaç $CO_2$ molekülü öngördüğünü hesaplayarak sırasıyla ekstrapolasyon ve interpolasyon kavramlarını örnekleyelim.
# 2030 yıilinda modelimiz bize ne kadar bir CO2 parcacik sayisi
# olacagini ongoruyor
# Ekstrapolasyon
x2030 = 2030 - 1960 # 1960dan beri gecen yil sayisi
a0 = sonucpar.params['a0'].value
a1 = sonucpar.params['a1'].value
a2 = sonucpar.params['a2'].value
CO2_2030 = a0 + a1*x2030 + a2*x2030**2
print("Parabol modelimiz {:d} yilinda milyon parcacik basına {:.2f} CO2 parcacigi olacagini ongormektedir.".\
format(x2030+1960,CO2_2030))
# Interapolasyon
x2005 = 2005 - 1960 # 1960dan beri gecen yil sayisi
CO2_2005 = a0 + a1*x2005 + a2*x2005**2
print("Parabol modelimiz {:d} yilinda milyon parcacik basına {:.2f} CO2 parcacigi oldugunu ongormektedir.".\
format(x2005+1960,CO2_2005))
Kaynaklar¶
Measurements and their Uncertainties, Ifan G. Hughes & Thomas P.A. Hase, Oxford University Press, 2010
Data Reduction and Error Analysis for the Physical Sciences, 3rd ed., Philip R.Bevington & D. Keith Robinson, 2003, McGraw Hill Higher Education
Numerical Analysis Using Matlab and Excel 3rd ed., Steven T. Karris, Orchard Publications, 2007
Numerical Methods for Engineers 6th ed., Steven C. Chapra, Raymond P. Canale, McGraw Hill, 2010
Numerical Methods, Rao V. Dukkipati, New Age International, 2010
Ascombe, F.J., 1973, The American Statistician, Vol. 27, No. 1. (Feb., 1973), pp. 17-21.