Önemli ölçüde kısıtlanmış kataloglarda bile çapraz eşleştirmenin uzun zaman aldığı açıktır. Bunun nedeni hesap etkinliği bakımından yetersiz bir algoritma olmasıdır. Çapraz eşleştiricinin uygulanma şekli, BSS'deki her nesne için SuperCOSMOS'taki her nesneye olan mesafenin hesaplanmasını gerektirir. Bu kısıtlanmış kataloglar arası çapraz eşleştirme bile 160 × 500 = 80.000 mesafe hesabını gerektirmektedir.
Her bir uzaklık hesabı birkaç mikrosaniye alırken, bu saniyeler veya dakikalar hızla birikir. Saniyeler başta önemsiz görünebilir, ancak kısıtlanmamış tam SuperCOSMOS kataloğunun bir önceki örnekte çalışılandan 250000 kat daha büyük olduğu ve 126 milyon nesne içerdiği düşünülürse hesap sayısı ve dolayısıyla süresinin ne kadar uzayacağını tahmin etmek zor değildir. SuperCOSMOS ile karşılaştırılabilir bir boyuta sahip AT20G BSS'den farklı bir katalog bununla çapraz eşleştirilmeye çalışıldığında bu yük içinden çıkılmaz hale gelebilir. Bunun gibi bir çapraz eşleştirme işlemi kişisel bir bilgisayarda günler hatta aylar alabilir.
Daha "akıllı" bir algoritmaya ihtiyacımız olacağı açıktır. Bir önceki uygulamada geliştirilen çapraz eşleştiricide, trigonometrik fonksiyonların doğru çalışabilmesi için $RA$ ve $DEC$'i radyana çevirmek gerekiyordu. Bu dönüşüm her seferinde cisimler arası uzaklığı hesaplayan fonksiyonunda yapılırsa, çapraz eşleştirme işlemi sırasında aynı koordinatlar birçok kez dönüştürülmüş olur.
Bir sonraki problemde, herhangi bir uzaklık hesabından önce dönüşümün yalnızca bir kez gerçekleşmesi için çapraz eşleştirici algoritmasının değiştirilmesi istenecektir. Zamandan yapılan bu küçük tasarruf bile önemlidir ve birikimli olarak toplam kod çalışma süresini etkiler.
Ayrıca geliştirilmesi istenen algoritma SuperCOSMOS vee AT20G BSS katalogları dışındaki kataloglara da uygulanabilir olmalıdır. Bu daha genel bir çözümdür ve istenen iki kataloğun birleştirilmesi için kullanılabilir.
Not: Bu uygulama coursera.org 'da University of Sydney tarafından verilen Data Driven Astronomy dersinden adapte edilmiştir.
Katalogların Yüklenmesi ve Yardımcı Fonksiyonlar:¶
Öncelikle çapraz eşleştirme uygulamasının "naif" bir versiyonu için yazılan yardımcı fonksiyonlar ve kullanılan katalogların karşılaştırmalar için uygun formatta Pandas veriçerçevelerine alınmasını sağlayan import fonksiyonlarını alıntılamaya ihtiyaç olacaktır.
import pandas as pd
import numpy as np
def import_bss(bss_dosya):
bss = pd.read_fwf(bss_dosya, header=None, usecols=range(1, 7))
bss['RA'] = np.zeros(len(bss[1]))
bss['DEC'] = np.zeros(len(bss[1]))
for i in range(len(bss[1])):
bss.at[i,'RA'] = hms2dec(bss.loc[i,1],bss.loc[i,2],bss.loc[i,3])
bss.at[i,'DEC'] = dms2dec(bss.loc[i,4],bss.loc[i,5],bss.loc[i,6])
bss.drop(range(1,7), axis=1, inplace=True)
return bss
def import_super(superCOSMOS_dosya):
sc = pd.read_csv(superCOSMOS_dosya, usecols=[0,1])
sc.rename(columns = {'Dec': 'DEC'}, inplace=True)
return sc
def hms2dec(h,m,s):
# HH:MM:SS yapisindaki sagacikligi
# derece biriminde decimal formata donusturen fonksiyon
if h > 24 or h < 0:
h %= 24
return 15*(h + m/60 + s/3600)
def dms2dec(d,m,s):
# DD:MM:SS yapisindaki sagacikligi
# derece biriminde decimal formata donusturen fonksiyon
if d > 90 or d < -90:
d %= 90
if d < 0:
return d - m/60 - s/3600
else:
return d + m/60 + s/3600
def angular_dist(ra1, dec1, ra2, dec2):
# Koordinatlari radyan biriminde verilen
# İki nokta arasi uzakligi Haversine formuluyle
# hesaplayan fonksiyon
a = np.sin(abs(dec1 - dec2)/2)**2
b = np.cos(dec1)*np.cos(dec2)*np.sin(abs(ra1 - ra2)/2)**2
d = 2*np.arcsin(np.sqrt(a + b))
return d
Soru-1:¶
Mikro optimizasyon¶
Derece cinsinden $RA$ ve $DEC$ 2-boyutlu dizilerini eşleştirmek üzere crossmatch isimli bir fonksiyon yazınız.
Fonksiyonunuz, çapraz eşleştirmeye başlamadan önce tüm koordinatları radyana çevirmelidir ve aşağıdaki 3 değeri döndürmelidir:
- Eşleştirilen cisimlerin ID'leri ve aralarındaki mesafeden oluşan demetlerin bir listesi;
- Birinci katalogda olup ikinciyle eşleşmeyen cisimlerin ID'lerinden oluşan bir liste;
- Fonksiyonun çalışmasının kaç saniye sürdüğünü gösteren bir kayan noktalı sayı.
Her iki katalog da 2-boyutlu NumPy dizileri olarak fonksiyona gönderilir. Her satır, tek bir nesnenin koordinatlarını içerir. Verinin ilk iki sütunu $RA$ ve $DEC$ iken cisim ID'leri 0'dan başlayarak sayılan satır numarasıdır.
time modülü fonksiyonlarından (perf_counter()) yararlanarak tüm işlemin kaç saniyede yapıldığını hesaplayan bir yapıyı fonksiyonunuza ekleyiniz ve bu hesap süresini de fonksiyondan döndürünüz.
# Cozum
import numpy as np
import time
def crossmatch(cat1, cat2, tolerans):
start = time.perf_counter()
matched = []
unmatched = []
cat1 = np.radians(cat1)
cat2 = np.radians(cat2)
tolerans = np.radians(tolerans)
for i in range(len(cat1['RA'])):
r = cat1.loc[i,'RA']
d = cat1.loc[i,'DEC']
minsep = angular_dist(r,d,cat2.loc[0,'RA'],cat2.loc[0,'DEC'])
idmin = 0
for j in range(len(cat2['RA'])):
angsep = angular_dist(r,d,cat2.loc[j,'RA'],cat2.loc[j,'DEC'])
if angsep < minsep:
minsep = angsep
idmin = j
if minsep < tolerans:
matched.append((i,idmin,np.degrees(minsep)))
else:
unmatched.append(i)
tot_time = time.perf_counter() - start
return matched,unmatched,tot_time
# Test fonksiyonu
if __name__ == '__main__':
cat1 = import_bss("veri/bss.dat")
cat2 = import_super("veri/superCOSMOS.csv")
tol = 40 / 3600. # 40 yaysaniyesi
matches, no_matches, time_taken = crossmatch(cat1, cat2, tol)
print('Eslesenler (Ilk 5) :', matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(matches))
print('Eslesmeyenler (Ilk 5) :', no_matches[:5])
print("Toplam eslesmeyen koordinat sayisi: ", len(no_matches))
print('Toplam sure:', time_taken)
$NumPy$ bu hesapları C ve Fortran dillerinde geliştirilmiş nümerik yapılardan faydalanarak yaptığı için Python listeleri üzerinde çalışmakta olan $for$ döngülerinden çok daha hızlıdır.
Listelerin elemanlarına tek tek uygulamak yerine tüm bir diziye uygulanan np.sqrt, np.sin, np.cos ve np.arcsin) fonksiyonları kullanılarak çapraz eşleştirmenin ikinci katalog içindeki (aşağıda) tarama bölümü
for id2, (ra2, dec2) in enumerate(cat2):
dist = angular_dist_rad(ra1, dec1, ra2, dec2)
if dist < min_dist:
min_dist = distaşağıdaki şekilde değiştirilecek olursa:
ra2s = cat2[:, 0]
dec2s = cat2[:, 1]
dists = angular_distance_rad(ra1, dec1, ra2s, dec2s)
min_dist = np.min(dists)Artık cisimler arası uzaklıkların hesaplanması, ikinci kataloğun tüm $RA$'ları ve $DEC$'leri üzerinde aynı anda gerçekleşir.
# Solution
# Write your crossmatch function here.
import numpy as np
import time
def crossmatch(cat1, cat2, tolerans):
start = time.perf_counter()
matched = []
unmatched = []
cat1 = np.radians(cat1)
cat2 = np.radians(cat2)
tolerans = np.radians(tolerans)
for i in range(len(cat1['RA'])):
r = cat1.loc[i,'RA']
d = cat1.loc[i,'DEC']
dists = angular_dist(r,d,cat2['RA'],cat2['DEC'])
minsep = np.min(dists)
idmin = np.argmin(dists)
if minsep < tolerans:
matched.append((i,idmin,np.degrees(minsep)))
else:
unmatched.append(i)
tot_time = time.perf_counter() - start
return matched,unmatched,tot_time
# Test fonksiyonu
if __name__ == '__main__':
cat1 = import_bss("veri/bss.dat")
cat2 = import_super("veri/superCOSMOS.csv")
tol = 40 / 3600. # 40 yaysaniyesi
matches, no_matches, time_taken = crossmatch(cat1, cat2, tol)
print('Eslesenler (Ilk 5) :', matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(matches))
print('Eslesmeyenler (Ilk 5) :', no_matches[:5])
print("Toplam eslesmeyen koordinat sayisi: ", len(no_matches))
print('Toplam sure:', time_taken)
Not: Hantal for döngüleri yerine NumPy dizileri ile çalışılması toplam çalışmas süresi neredeyse 1 / 10'una düşürmüştür!
Tekrarlardan kaçınmak¶
Yapılabilecek bir diğer optimizasyon, ikinci katalogdaki cisimleri, o anda eşleştirilmekte olan ilk katalog cisminden uzak bir DEC değerine sahipse gözardı etmektir. Bun yapmak için
Diziyi ID yerine DEC'e göre sıralayıp ikinci katalog cisimlerini taramak,
Ulaşılan DEC değerleri arananı maksimum toleranstan fazla geçtiğinde aramayı durdurmak
iyi bir çözümdür.
Örneğin, $\delta$ dikaçıklıklı bir ilk katalog cismi (hedef) olduğunu ve maksimum eşleşme yarıçapının da $r$ olarak belirlendiğini varsayalım. Yeni algoritma, döngüden çıkmadan önce yalnızca $-90$ (başlangıç) ile $\delta + r$ derece arasındaki deklinasyona sahip ikinci katalog cisimleri üzerinde çalışacaktır. Bu da ortalamada kataloğun neredeyse yarısının hiç taranmayacağı anlamına gelir ki önemli bir kazançtır. Bu tekrar döngü yapısını kullanmayı gerektirse de performans açısından fayda sağlayıp sağlamayacağını denetlemekte fayda vardır.
Soru-3:¶
Aramayı daraltma¶
crossmatch fonksiyonunu 2. kataloğu deklinasyonda sıralayıp sadece tolerans limitleri dahilinde arama yapılacak şekilde düzenleyiniz. Sıralama işini Pandas veriçerçevelerine ve serilerine uygulanabilen sort_values fonksiyonuyla yapmak çok daha kolaydır; çünkü sıralama sonrası satırların (cisim ID'lerinin) orjinal indeksleri korunur! Ancak ikinci katalogdaki $RA$ ve $DEC$ değerlerini karşılaştırmalar ve tarama için NumPy dizilerine dönüştürürken bu indeksleri de bir NumPy dizisine almak gerekecektir.
# Cozum
import numpy as np
import time
def crossmatch(cat1, cat2, tolerans):
start = time.perf_counter()
matched = []
unmatched = []
cat1 = np.radians(cat1)
cat2 = np.radians(cat2)
tolerans = np.radians(tolerans)
cat2_sorted = cat2.sort_values(by='DEC')
# tarama ve karsilastirma icin numpy dizileri
ra2 = np.array(cat2_sorted['RA'])
dec2 = np.array(cat2_sorted['DEC'])
# orjinal indeksler
ind2 = np.array(cat2_sorted.index)
for i in range(len(cat1['RA'])):
r = cat1.loc[i,'RA']
d = cat1.loc[i,'DEC']
minsep = angular_dist(r,d,ra2[0],dec2[0])
idmin = ind2[0]
for j in range(len(ra2)):
angsep = angular_dist(r,d,ra2[j],dec2[j])
if angsep < minsep:
minsep = angsep
idmin = ind2[j]
if dec2[j] > d + tolerans:
break
if minsep < tolerans:
matched.append((i,idmin,np.degrees(minsep)))
else:
unmatched.append(i)
tot_time = time.perf_counter() - start
return matched,unmatched,tot_time
# Test fonksiyonu
if __name__ == '__main__':
cat1 = import_bss("veri/bss.dat")
cat2 = import_super("veri/superCOSMOS.csv")
tol = 40 / 3600. # 40 yaysaniyesi
matches, no_matches, time_taken = crossmatch(cat1, cat2, tol)
print('Eslesenler (Ilk 5) :', matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(matches))
print('Eslesmeyenler (Ilk 5) :', no_matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(no_matches))
print('Toplam sure:', time_taken)
Görüldüğü gibi her ne kadar full taramaya göre süre açısından önemli bir avantaj sağladıysa da bu çözüm, for döngüsü kullanmaksızın NumPy dizilerine doğrudan dayanan çözüme göre bir miktar daha uzun sürmüştür. Bu durum aranan değerin daha erken bulunabileceği durumlar için daha kısa çalışma süreleri getirerek uzun vadede pek çok başka katalog eşleştirmeleri için daha avantajlı dahi olabilir. Ayrıca NumPy dizilerine dönüşümler gibi bazı ek işlemlerin de koda eklenmiş olduğu dikkate alınmalıdır.
Binary search¶
Aranan deklinasyon değerini tolerans kadar geçtikten sonra aramayı durdurmakla kalmayıp, aramayı aradığımız cisme mümkün olduğunca yakın başlatarak önceki optimizasyonu daha da geliştirebiliriz. Bunun için
- İkinci katalog cisimlerini deklinasyon sırasına göre sırala;
- Aramayı ikinci katalogda $\delta - r$ değerinden büyük deklinasyondan başlat;
- İkince katalogda aramayı $\delta + r$ değerinde sonlandır.
Aramayı bu şekilde daraltmak performansı önemli ölçüde arttıracaktır.
$[\delta - r, \delta + r]$ sınırlarına en yakın ikinci katalog nesnelerini bulmanın hızlı bir yolunu bulmamız gerekiyor, böylece aramaya nereden başlayıp nerede bitirileceği belirlenmiş olur. Aksi takdirde yine tarayarak bu değerlere erişilmiş olunur ki tarama yapılmış olacağı için istenen bu değildir ve performans artışı da getirmeyecektir.
Bunu yapmanın çok etkin bir yolu "ikili arama" (ing. binary search) algoritmasından faydalanmaktır.
İkili arama algoritması sıralı bir listede aranan elemanın indeks değerini bulmak için listedeki tüm değerlerle tek tek karşılaştırmadan çok daha etkilidir. İkili arama, listeyi art arda ikiye bölerek sadece aranan nesneyi içerebilecek yarıya ulaşılanan kadar aramayı sürdürür.
Aşağıdaki listede 15 sayısının bulunması örnek olarak verilebilir:
# 0 1 2 3 4 5 6 7 8 9
s = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]- Bu listenin ortasındaki değer $s[4] = 14$ 'tür.
- 14 değeri 15'ten küçük olduğundan, 15 $s[5:10]$ diliminde olmalıdır.
- $s[5:10]$'un ortası $s[7] = 17$'dir.
- 17 değeri 15'ten büyüktür, öyleyse 15 $s[5:7]$ diliminde olmalıdır.
- $s[5:7]$ 'nin orta değeri $s[5] = 15$ 'tir.
- 15 aradığımız değer olup indeksi 5'tir.
Bu, 10'dan 19'a kadar olan bir listede 15'i bulmanın dolambaçlı bir yolu gibi görünüyor, ancak yalnızca 3 karşılaştırmanın yapıldığını, ancak tüm liste aransa 6 karşılaştırmanın yapılacağı unutulmamalıdır. Büyük dizilerde bu tür küçük tasarruflar önemli fark yaratabilir. Doğrudan arama ile 1000 uzunluğundaki bir listedeki bir öğeyi bulmak için ortalama olarak 500 karşılaştırma gerekliyken, ikili aramada yalnızca 10 karşılaştırma gereklidir.
Numpy ve İkili Arama Algoritması¶
NumPy modülünün searchsorted fonksiyonu (aynı fonksiyon Pandas modülünde de bulunmaktadır) bu algoritmayla arama yapar. Fonksiyonun nasıl kullanıldığı aşağıda örneklenmiştir.
######0 1 2 3 4 5 6 7 8 9
s = [10, 11, 12, 13, 14, 15, 16, 17, 18, 19]
index = np.searchsorted(s, 15, side='left')
print(index)
################0 1 2 3 4 5 6 7 8 9
s = pd.Series([10, 11, 12, 13, 14, 15, 16, 17, 18, 19])
index = s.searchsorted(15, side='left')
print(index)
Aynı dizide aranan değerden birden fazla farsa (örneğin 15 değerinden) side='left' ayarı yapıldığında ilk bulunan değerin (15)'in, side='right' yapılırsa son bulunan değerin (15) indeksi döndürülür.
Soru-4:¶
Aramayı Daraltma¶
crossmatch fonksiyonunu ikinci katalogda sadece $dec1 - tolerans$ ile $dec1 + tolerans$ arasındaki değerleri ikili arama yapacak şekilde düzenleyiniz. searchsorted fonksiyonu hem aramanın yapılacağı $dec1 - tolerans$, hem de döngüden çıkılacak $dec1 + tolerans$ değerlerini bulmak için kullanılmalıdır.
# Cozum
import numpy as np
import time
def crossmatch(cat1, cat2, tolerans):
start = time.perf_counter()
matched = []
unmatched = []
cat1 = np.radians(cat1)
cat2 = np.radians(cat2)
tolerans = np.radians(tolerans)
cat2_sorted = cat2.sort_values(by='DEC')
ra2 = np.array(cat2_sorted['RA'])
dec2 = np.array(cat2_sorted['DEC'])
ind2 = np.array(cat2_sorted.index)
for i in range(len(cat1['RA'])):
r = cat1.loc[i,'RA']
d = cat1.loc[i,'DEC']
index_start = np.searchsorted(dec2, d - tolerans,side='left')
index_stop = np.searchsorted(dec2, d + tolerans, side="left")
minsep = angular_dist(r,d,ra2[index_start],dec2[index_start])
idmin = ind2[index_start]
for j in range(index_start,index_stop):
angsep = angular_dist(r,d,ra2[j],dec2[j])
if angsep < minsep:
minsep = angsep
idmin = ind2[j]
if minsep < tolerans:
matched.append((i,idmin,np.degrees(minsep)))
else:
unmatched.append(i)
tot_time = time.perf_counter() - start
return matched,unmatched,tot_time
# Test fonksiyonu
if __name__ == '__main__':
cat1 = import_bss("veri/bss.dat")
cat2 = import_super("veri/superCOSMOS.csv")
tol = 40 / 3600. # 40 yaysaniyesi
matches, no_matches, time_taken = crossmatch(cat1, cat2, tol)
print('Eslesenler (Ilk 5) :', matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(matches))
print('Eslesmeyenler (Ilk 5) :', no_matches[:5])
print("Toplam eslesmeyen koordinat sayisi: ", len(no_matches))
print('Toplam sure:', time_taken)
Çalışma süresi bu kez önemli miktarda azalmıştır (1/25 civarında). Büyük boyutlu katalogların karşılaştırılmasında bu algoritmanın ne kadar büyük bir avantaj sağlayacağı açıktır.
k-d Ağaçları¶
Çapraz eşleştirme, astronomide sıklıkla yapıaln bir işlem olduğundan optimize edilmiş uygulamalarının zaten kodlanmış olması doğaldır. Astropy modülü k-d ağaçlarına dayalı bir çapraz korelasyon fonksiyonunu bu amaçla sunmaktadadır.
Astropy, içinde arama yapılan ikinci katalogdan bir k-d ağacı oluşturarak, ilk katalogdaki her cisim için ikili aramaya benzer bir şekilde bir eşleşme arar. Bu algoritmada k-boyutlu uzay, her seferinde bölümün bir tarafı yalnızca tek bir cisim içerene kadar özyinelemeli (recursive) olarak iki parçaya bölünür.
Katalog eşleştirme uygulamasında bu algoritma;
Sağaçıklığın ortanca (medyan) değerini bul, kataloğu bunun sağı ve solundan ikiye böl.
Her bölümde deklinasyonun ortanca değerini bul, bölümü bunun aşağı ve yukarısından ikiye böl.
Bu bölümlerin her birinde sağaçıklığın ortanca (medyan) değerini bul, bu bölümü bunun sağı ve solundan ikiye böl.
2 ve 3. adımları her bölümde tek bir nesne kalıncaya kadar sürdür.
Bu algoritma içinde arama yapılacak aşağıdaki şekilde bir ikili ağaç oluşturur.
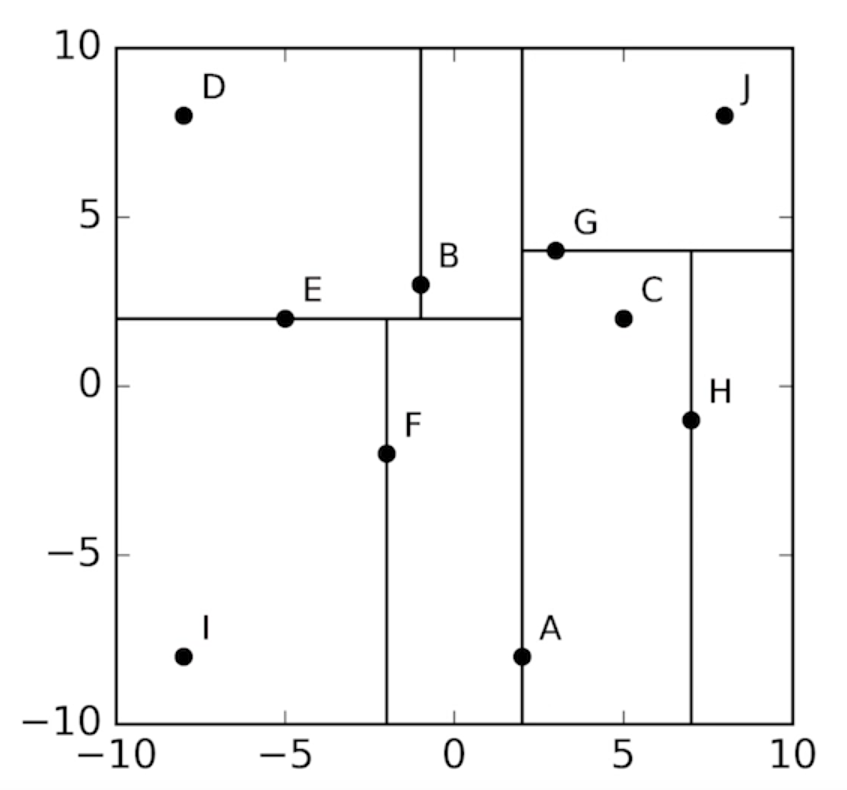
Yukarıdaki şekilde 10 cisimden 6. sı olan $A$ sağ açıklıktaki medyan (ortanca) olarak seçilebilir (5 de seçilebilirdi ama sağdaki (daha büyük sağ açıklık değerine sahip olan tercih edilir.). Buradan yapılacak bir bölme sonrası, bu değerin sol ya da sağ tarafına geçilerek ilerlenebilir. Sol tarafa geçilecek olunursa oradaki 5 koordinatın deklinasyonda ortancası $E$'dir. Buradan bölündükten sonra üst ya da alt tarafa geçilerek devam edilebilir. Bu bölmenin üst tarafına geçilecek olursa iki koordinat kaldığı görülür ($D$,$B$); medyan olarak bunlardan sağ açıklığı büyük olan $B$ koordinatı seçilir. Burada deklinasyon ekseninde ilerlenebilecek bir düğüm kalmamıştır; zira $D$ tek başınadır ve alt bölmeye geçilir. Alt bölmenin sağ açıklıktaki medyanı sağ açıklığı büyük olan $F$ olarak belirlenir. Daha sonra $A$'nın sağ tarafına geçilir. Bu bölmede bulunan 4 koordinattan deklinasyonda daha büyük olan $G$ medyan olarak belirlenir. Bunun üzerinde tek bir nokta kalmış olduğundan alt bölmeye inilir ve sağ açıklıkta daha büyük olan $H$ medyan olarak belirlenir. Bunun sol tarafında sadece bir koordinat kaldığından ağaç yapısı tamamlanmış olur.
k-d Ağaçları İçinde Arama¶
k-d ağacı oluşturulduktan sonra arama aşağıdaki şekilde yapılır.
Aranan cisimle en yüksek seviyedeki düğüm (kök düğüm) arasındaki uzaklığı hesapla, ardından bu düğüme sağ açıklıkta en yakın alt düğüme git,
Aranan cisimle bu düğümdeki (child) cisim arasındaki uzaklığı hesapla, ardından bu alt düğüme dik açıklıkta en yakın alt düğüme git,
Arnanan cisimle bu düğümdeki (child) cisim arasındaki uzaklığı hesapla, ardından alt düğüme sağ açıklıkta en yakın alt düğüme git,
2-3 arasındaki adımları artık alt düğüm (child) kalmayıncaya kadar tekrarla ve en alt düğüme (leaf node) ulaş,
Hesaplanan tüm uzaklıkların en kısasını bul, bu uzaklık aranan cisme ikinci katalogdaki en yakın cismin uzaklığıdır.
Her bir düğüm iki "çocuk" düğüme ayrıldığı için
$N$ cisim için "kökten" (root) "yaprağa" (leaf) $log_2(N) $ düğümde inilir. Bu şekilde SuperCOSMOS kataloğu gibi 250 million cisim içeren bir kataloda yalnız 28 uzaklık hesabı yeterli olmaktadır!
Aşağıdaki şekilde koordinatları bilinen $T$ cismine k-d ağacına dönüştürülen bir katalogdaki en yakın cisim aranmaktadır.
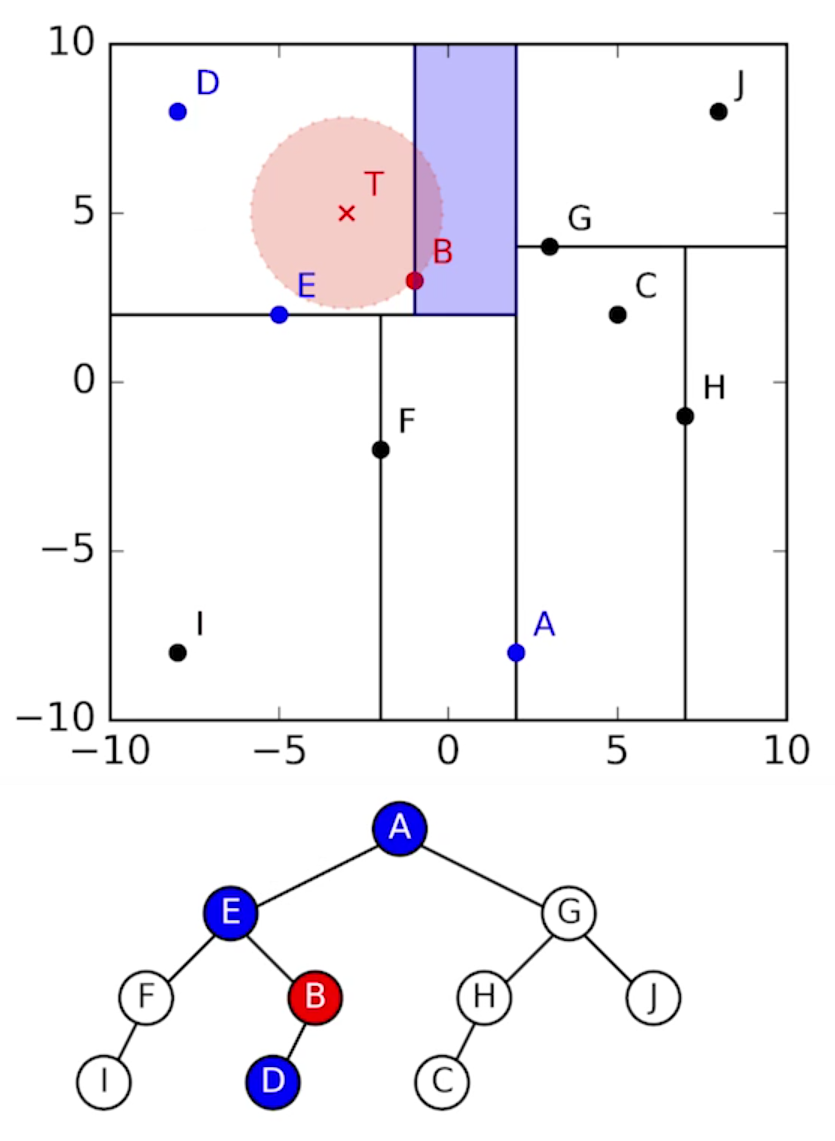
$T$ cismi ile öncelikle kök düğümdeki cisim ($A$) arasındaki uzaklık hesaplanır. Daha sonra $A$'ya sağaçıklıkta en yakın alt düğümdeki cisme ($E$) gidilir ve bununla $T$ cismi arasındaki mesafe hesaplanır. Bu uzaklık $A$'ya uzaklığa göre büyük olduğundan bu kez $E$'ye deklinasyonda en yakın cismin bulunduğu alt düğüme geçilir. Bu cisim $B$'dir. $B$ ile $T$ arasındaki uzaklık $E$ ile olandan küçüktür ve devam edilir. Bu kez $B$'ye sağ açıklıkça en yakın alt düğüme gidilir. Bu alt düğümde $D$ bulunmaktadır. $D$ ile $T$ arasındaki mesafe $B$ ile olana göre büyüktür. $T$ cismine k-d ağacına dönüştürülmüş katalogdaki en yakın cisim $B$ olarak 4 karşılaştırma 5 uzaklık ölçümü sonrası bulunmuş olur. Eğer bu cisim istenen bir yarıçap içindeyse $T$ cismi ile eşleşen bir cisim olarak değerlendirilebilir.
Astropy ile bu şekilde yapılan bir arama aşağıda örnek olarak verilmiştir.
from astropy.coordinates import SkyCoord
from astropy import units as u
coords1 = [[270, -30], [185, 15], [120, -10], [50, 25], [300,5]]
coords2 = [[185, 20], [280, -30], [45, 20], [295, 0], [100, -15]]
sky_cat1 = SkyCoord(coords1*u.degree, frame='icrs')
sky_cat2 = SkyCoord(coords2*u.degree, frame='icrs')
closest_ids, closest_dists, closest_dists3d = sky_cat1.match_to_catalog_sky(sky_cat2)
print(closest_ids)
print(closest_dists)
SkyCoord nesnesi, Astropy'ın gökyüzü kataloğu nesnesidir. Birimleri (burada derece cinsinden u.degree ile verilmiştir) ve bir referans çerçevesi (burada ICRS) belirtildiği sürece her koordinat dizisiyle çalışırlar. International Celestial Reference System esasen ekvatoral koordinatlardan oluşan bir katalogdur.closest_id ve closest_dists çıktıları, sky_cat1'de olup sky_cat2 'deki bir cisim eşleşen cismin sky_cat2 içindeki satır indeksini ve ona olan uzaklığını verir.closest_dists açısal uzaklık closest_dists3d ise 3-boyuttaki uzaklıktır.
Not:¶
Astropy uzaklık değerlerini Quantity nesnesi olarak döndürür. Bu nesne türü bir NumPy dizisine çevrilirken bu nesnenin değerini value metodu ile almak yeterlidir; birimi de akılda tutmakta fayda vardır.
closest_dists_array = closest_dists.valueSoru-5¶
crossmatch fonksiyonunu Astropy fonksiyonalitesiyle arama yapacak şekilde düzenleyiniz.
# Cozum
import numpy as np
import time
from astropy.coordinates import SkyCoord
from astropy import units as u
def crossmatch(cat1, cat2, tolerans):
start = time.perf_counter()
matched = []
unmatched = []
cat1 = SkyCoord(ra=cat1['RA']*u.degree, dec=cat1['DEC']*u.degree, frame="icrs")
cat2 = SkyCoord(ra=cat2['RA']*u.degree, dec=cat2['DEC']*u.degree, frame="icrs")
closest_ids, closest_dists, _ = cat1.match_to_catalog_sky(cat2)
for i,j in enumerate(closest_ids):
angsep = closest_dists[i].value
if angsep < tolerans:
matched.append((i, j, angsep))
else:
unmatched.append(i)
tot_time = time.perf_counter() - start
return matched,unmatched,tot_time
# Test fonksiyonu
if __name__ == '__main__':
cat1 = import_bss("veri/bss.dat")
cat2 = import_super("veri/superCOSMOS.csv")
tol = 40 / 3600. # 40 yaysaniyesi
matches, no_matches, time_taken = crossmatch(cat1, cat2, tol)
print('Eslesenler (Ilk 5) :', matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(matches))
print('Eslesmeyenler (Ilk 5) :', no_matches[:5])
print("Toplam eslesen koordinat sayisi: ", len(no_matches))
print('Toplam sure:', time_taken)
Sonuç olarak hızlı olmakla birlikte ikili aramaya dayanan bir önceki çözümden neredeyse 5 kat yavaş sürdü ancak daha uzun boyutlu katalogların karşılaştırılması için kullanıldığında bir performans avantajı sağlayacaktır. Kataloglar $RA$ ya da $DEC$'e göre sıraladığınızda daha hızlı sonuç elde edildiğini deneyerek görebilirsiniz!